9.2 RSA算法

最新推荐文章于 2024-11-30 15:00:48 发布

夏驰和徐策

最新推荐文章于 2024-11-30 15:00:48 发布

阅读量1.5k

点赞数 27

分类专栏：密码编码学与网络安全——原理与实践文章标签：算法网络安全密码学

本文链接：https://blog.csdn.net/tang7mj/article/details/135354086

版权

密码编码学与网络安全——原理与实践专栏收录该内容

58 篇文章

订阅专栏

思维导图：

深入理解9.2 RSA算法

引言： RSA算法是一种非对称加密算法，广泛应用于数据传输和数字签名等多种安全领域。它由Ron Rivest、Adi Shamir 和Leonard Adleman在1978年共同提出。RSA的安全性基于大数分解的难度，直到今天，没有有效的算法能在实际时间内分解非常大的数。

1. 原理简介： RSA算法基于一个简单的数论事实：将两个大质数相乘很容易，但要将其乘积分解回原来的两个质数却极其困难。在RSA中，每个人都有一对密钥：公钥和私钥。公钥用于加密数据，而私钥用于解密。由于加密和解密使用的是不同的密钥，这就是所谓的非对称加密。

2. 密钥生成：

选择两个大的随机质数p和q，计算N=p∗q。N的长度，即其位数，是密钥的长度。
计算欧拉函数ϕ(N)=(p−1)∗(q−1)。
选择一个整数e，使得e与ϕ(N)互质，并且1<e<ϕ(N)。
计算e对于ϕ(N)的模逆元d，即d∗e≡1modϕ(N)。

公钥是(N,e)，私钥是(N,d)。

3. 加密与解密：

加密：对于明文消息M，密文C计算为C≡MemodN。
解密：已知密文C，计算明文M为M≡CdmodN。

4. 安全性分析： RSA的安全性依赖于大数分解的困难。只要p和q足够大，用当前的算法和计算能力，分解N是不可行的。然而，如果能找到一种有效的大数分解算法，或者能够利用量子计算机来分解大数，RSA的安全性将不复存在。

5. 实际应用： RSA算法广泛应用于数字签名、SSL/TLS协议、电子邮件加密等领域。它是当今数字世界中保护数据安全不可或缺的工具之一。

结论： 尽管存在潜在的安全风险，RSA算法仍然是目前最广泛使用的公钥加密算法。它的安全性、简洁和有效性使其成为保护在线通信不可或缺的工具。

9.2 RSA算法

背景:

Diffie和Hellman首次提出公钥密码学概念。
RSA算法由MIT的Rivest, Shamir, Adleman提出，是最早和最著名的实现。
早期其他算法如Merkle的背包密码后来都被破解，但RSA证明相对稳固。

核心原理:

RSA是基于大数分解难题的非对称加密算法。
它包括两个关键部分：加密和解密。
加密和解密操作基于模幂运算。

关键组件:

两个大的素数p和q，和它们的乘积n=p⋅q，这决定了密钥的长度。
公钥为(e,n)，私钥为(d,n)，其中e是加密指数，d是解密指数。
明文和密文都是0至n−1之间的整数。

加密和解密过程:

选择两个大素数p和q，计算n=p⋅q和ϕ(n)=(p−1)⋅(q−1)。
选择一个与ϕ(n)互质的小整数e。
计算e的模ϕ(n)的逆元d。
公钥为(e,n)，私钥为(d,n)。
加密：C=Memodn。
解密：mod M=Cdmodn。

安全性和实际应用:

安全性基于大数分解难题。
广泛应用于数字签名、安全通信等。

注意点:

选择合适的e和d至关重要。
n的大小直接影响安全性和计算效率。

示例:

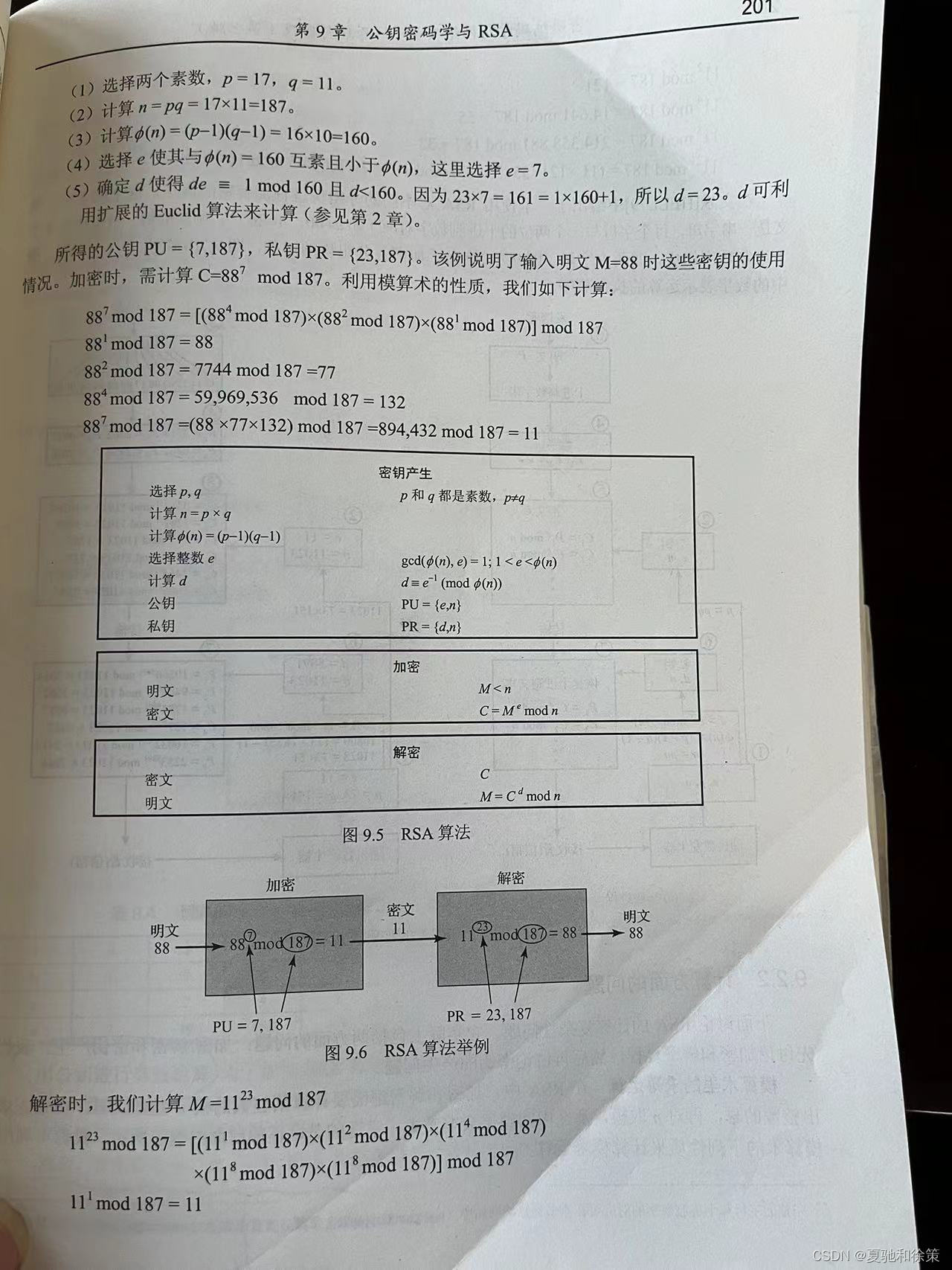
选择p=17和 q=11，计算n=187和ϕ(n)=160。
选择e=7，计算d=23。
公钥为(7,187)(7,187)，私钥为(23,187)(23,187)。
加密和解密示例：M=88，加密得到C=11，解密回到M=88。

9.2.2 计算方面的问题

加密/解密和密钥产生:

RSA的计算复杂性主要涉及两个方面：加密/解密和密钥产生。
首先讨论加密和解密过程，这涉及到模幂运算的效率问题。

模幂运算:

在RSA中，加密和解密都涉及模n的整数次幂运算。
直接计算会导致非常大的中间结果，但可以通过模算术性质简化这个过程。

效率提升:

为提升计算效率，可采用快速模幂算法，减少必要的乘法次数。
例如，通过分解指数并逐步计算中间结果的平方，可以有效减少运算步骤。

特定的指数选择:

为了加快使用公钥的运算速度，通常会选择特定的e值，如65537。
但需注意，如果指数太小，如e=3，RSA可能遭受简单攻击。

中国剩余定理 (CRT) 应用:

利用CRT可以加快私钥运算的速度，通过定义中间结果和预先计算，使得解密过程大约快4倍。

密钥产生过程:

选择素数 p 和 q: 从大集合中选取以避免穷举攻击。
素性测试: 采用概率素性测试方法，如Miller-Rabin算法，确定大整数是否为素数。
选择 e: 选择与ϕ(n)互素的e，计算d。
随机性和确定性: 确定素数和e的过程涉及随机数生成和概率测试。

效率和安全性的平衡:

选择小指数可提升效率，但可能降低安全性。
使用CRT和快速模幂算法可以在不牺牲安全性的前提下提升效率。

总结:

RSA加密和解密的计算复杂性是可管理的，通过算法优化和数学工具可以显著提高效率。
密钥产生是一个涉及随机数和概率测试的复杂过程，但它确保了系统的安全性。

9.2.3 RSA的安全性

潜在攻击方式:

穷举攻击: 尝试穷举所有可能的私钥。
数学攻击: 试图分解两个素数的乘积n。
计时攻击: 依赖于解密算法的运行时间。
基于硬件故障的攻击: 利用处理器发生的故障。
选择密文攻击: 利用RSA算法的性质。

对策:

使用大密钥空间以抵抗穷举攻击，但这会增加计算复杂性，从而降低系统运行速度。

数学攻击详解:

分解n为两个素因子p和q，从而计算出ϕ(n)和最终确定d。
直接确定ϕ(n)而不先确定p和q，同样可以确定d。
直接确定d，而不先确定ϕ(n)。

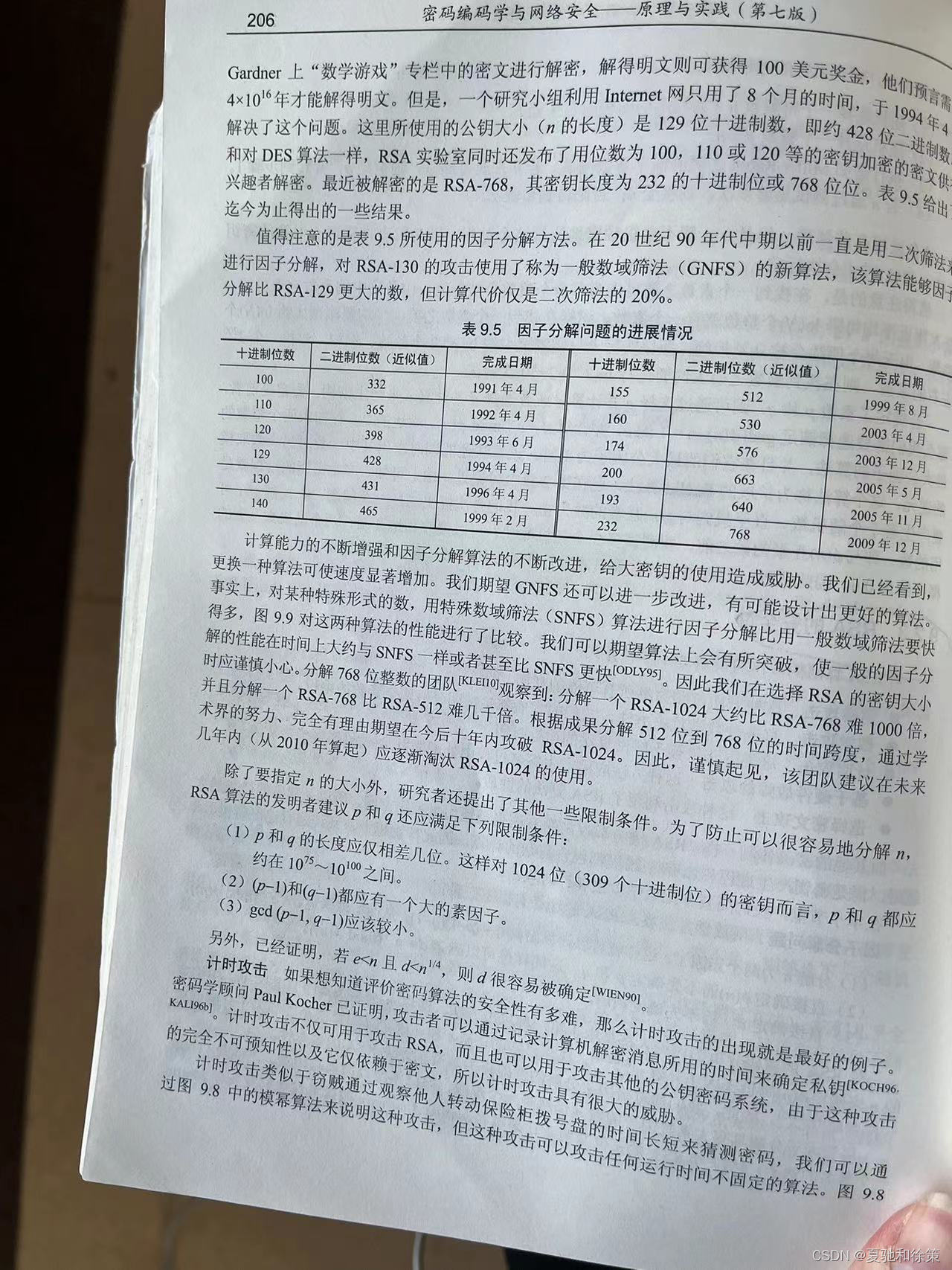
因子分解问题:

因子分解n是一个已知难题，但随着计算能力的增强和算法的改进，以前认为安全的密钥长度可能不再安全。
例如，RSA-129曾被认为几乎无法破解，但后来在8个月内被解决。
进展表明，因子分解算法越来越高效，需要的时间大大减少。

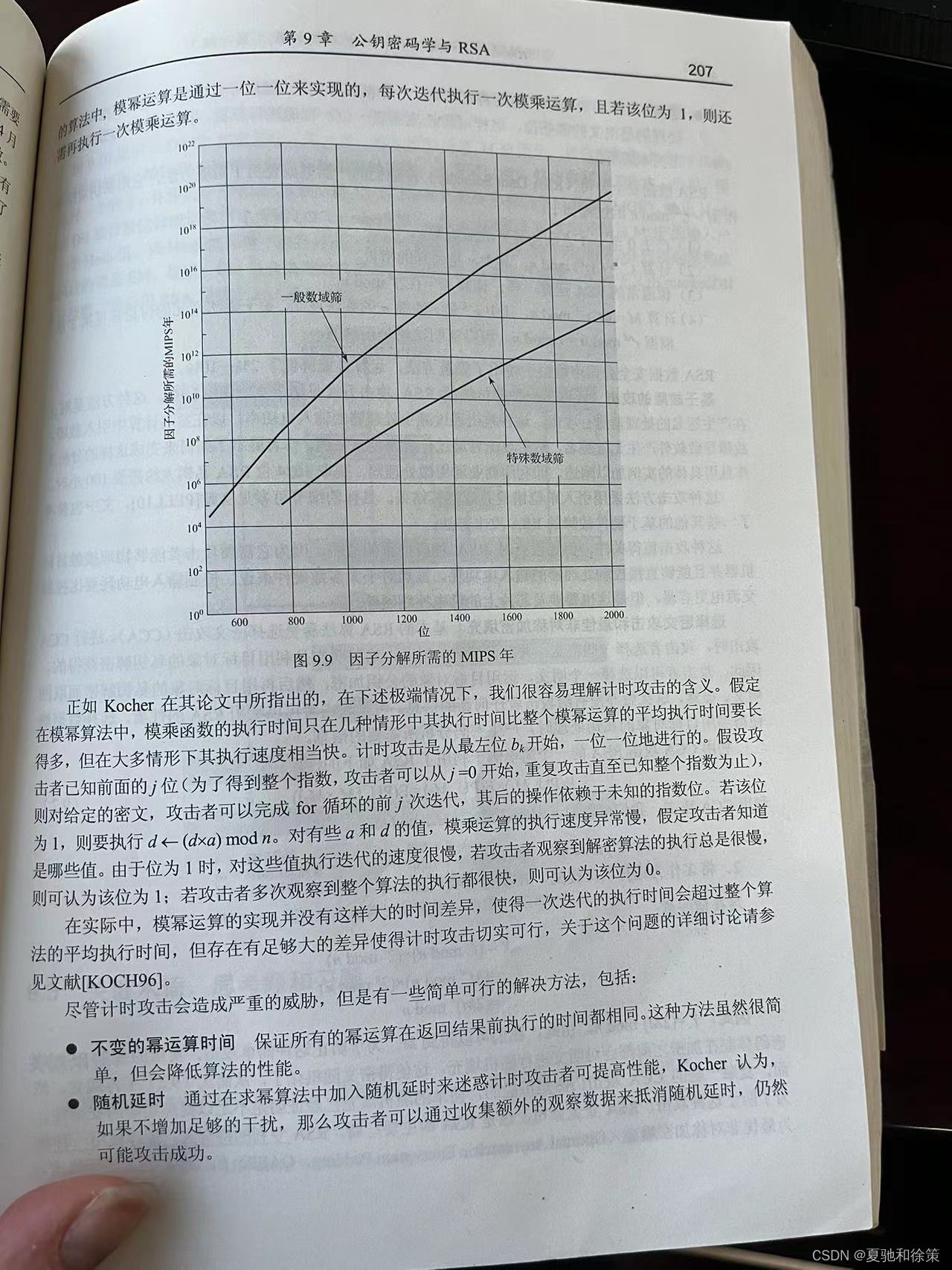
计算能力和算法进步的影响:

随着计算能力的提升和因子分解算法的改进，RSA的安全性受到挑战。
选择合适的密钥大小非常关键，以保持安全性。

计时攻击详解:

攻击者通过测量解密操作的时间来推断私钥。
这种攻击表明密码算法的实现应该避免根据密钥的不同而有显著的时间差异。

对策:

保证所有幂运算的执行时间相同。
加入随机延时以迷惑攻击者。
在执行幂运算之前将密文乘以随机数。

基于故障的攻击:

通过在签名计算中引入故障来恢复私钥。
需要攻击者能够物理接触并控制目标机器。

选择密文攻击与OAEP:

基本的RSA算法易受选择密文攻击，攻击者可以选择密文以获得解密的明文。
最优非对称加密填充(OAEP)是一种用来改善RSA安全性的技术。

总结：

重点:

潜在攻击方式: 理解RSA面临的五种主要攻击方式（穷举攻击、数学攻击、计时攻击、基于硬件故障的攻击、选择密文攻击）及其原理。
数学攻击：特别关注数学攻击，这是RSA安全性的核心，主要涉及分解n为两个素因子p和q的难题。
因子分解问题的进展: 了解因子分解算法的历史和进展，以及这对RSA密钥长度选择的影响。
计时攻击的机理与对策: 理解计时攻击是如何利用算法执行时间的差异进行私钥推断的，以及常见的防御措施。
选择密文攻击与OAEP: 理解基本RSA易受选择密文攻击的问题和最优非对称加密填充(OAEP)的改进方法。

难点:

数学攻击的细节: 理解数学攻击背后的数学原理可能相对复杂，特别是涉及到大数分解的算法。
因子分解的算法进展: 跟踪和理解因子分解算法的最新进展可能需要较深的数学和计算机科学背景。
计时攻击的具体实现: 理解计时攻击的具体实现和防御措施需要深入了解算法的实际执行过程和环境。

易错点:

忽视密钥大小的重要性: 在实践中，可能会低估选择足够大密钥大小的重要性，这可能会使RSA系统容易受到攻击。
混淆不同攻击方式的原理和影响: 每种攻击方式有其独特的原理和影响，混淆它们可能会导致对RSA安全性的误解。
过分依赖单一防御措施: 依赖单一防御措施（如仅增加密钥长度）而忽视其他潜在攻击方式和防御措施是一个常见错误。