
8.13.9 ACM-ICPC 多项式与生成函数: 常系数齐次线性递推
本节介绍常系数齐次线性递推的相关内容。具体包括以下几个部分:
- 齐次线性递推的定义
- 齐次线性递推方程的求解方法
- 特征多项式及其作用
- 递推关系的具体例子
- 代码实现与算法优化
齐次线性递推的定义
常系数齐次线性递推是指一个递推关系,其中每一项由前几项的线性组合表示,且组合系数是常数。其一般形式为:
an=c1an−1+c2an−2+⋯+ckan−ka_n = c_1 a_{n-1} + c_2 a_{n-2} + \cdots + c_k a_{n-k}an=c1an−1+c2an−2+⋯+ckan−k
其中,c1,c2,…,ckc_1, c_2, \ldots, c_kc1,c2,…,ck 为常系数,ana_nan 为第 nnn 项。
求解方法
解决常系数齐次线性递推问题的关键在于找到通项公式。通常通过以下步骤实现:
-
构造特征多项式:设递推关系为 an=c1an−1+c2an−2+⋯+ckan−ka_n = c_1 a_{n-1} + c_2 a_{n-2} + \cdots + c_k a_{n-k}an=c1an−1+c2an−2+⋯+ckan−k,其对应的特征多项式为:
P(x)=xk−c1xk−1−c2xk−2−⋯−ckP(x) = x^k - c_1 x^{k-1} - c_2 x^{k-2} - \cdots - c_kP(x)=xk−c1xk−1−c2xk−2−⋯−ck
-
求解特征方程:求特征多项式 P(x)=0P(x) = 0P(x)=0 的根。设根为 r1,r2,…,rmr_1, r_2, \ldots, r_mr1,r2,…,rm,每个根的重数分别为 α1,α2,…,αm\alpha_1, \alpha_2, \ldots, \alpha_mα1,α2,…,αm。
-
构造通项公式:根据特征方程的根,构造递推关系的通项公式。对于单根 rir_iri,通项公式中对应的部分为 AirinA_i r_i^nAirin;对于重根 rir_iri(重数为 αi\alpha_iαi),通项公式中对应的部分为 (Bi0+Bi1n+Bi2n2+⋯+Bi(αi−1)nαi−1)rin(B_{i0} + B_{i1} n + B_{i2} n^2 + \cdots + B_{i(\alpha_i-1)} n^{\alpha_i-1}) r_i^n(Bi0+Bi1n+Bi2n2+⋯+Bi(αi−1)nαi−1)rin。
特征多项式及其作用
特征多项式在求解常系数齐次线性递推中起到关键作用。通过特征多项式的根,可以将递推关系转化为求解特征方程的问题,从而利用代数方法求得递推关系的通项公式。
递推关系的具体例子
例子1:斐波那契数列
斐波那契数列是常系数齐次线性递推的一个经典例子,其递推关系为:

对应的特征多项式为:
P(x)=x2−x−1P(x) = x^2 - x - 1P(x)=x2−x−1
求解特征方程 x2−x−1=0x^2 - x - 1 = 0x2−x−1=0,得根为:
r1=1+52,r2=1−52r_1 = \frac{1 + \sqrt{5}}{2}, \quad r_2 = \frac{1 - \sqrt{5}}{2}r1=21+5,r2=21−5
因此,斐波那契数列的通项公式为:

例子2:线性递推
考虑递推关系:

对应的特征多项式为:
P(x)=x2−2x+1P(x) = x^2 - 2x + 1P(x)=x2−2x+1
求解特征方程 x2−2x+1=0x^2 - 2x + 1 = 0x2−2x+1=0,得根为:
r=1r = 1r=1
由于是重根,通项公式为:

代码实现与算法优化
为了在程序中高效实现常系数齐次线性递推,可以使用矩阵快速幂的方法。以下是一个示例代码,展示了如何使用矩阵快速幂求解斐波那契数列:
#include <iostream>
#include <vector>
using namespace std;
typedef vector<vector<long long>> matrix;
const long long MOD = 1e9 + 7;
matrix multiply(const matrix &A, const matrix &B) {
matrix C(2, vector<long long>(2));
for (int i = 0; i < 2; ++i)
for (int j = 0; j < 2; ++j)
for (int k = 0; k < 2; ++k)
C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % MOD;
return C;
}
matrix power(matrix A, long long n) {
matrix result = {{1, 0}, {0, 1}};
while (n > 0) {
if (n % 2 == 1)
result = multiply(result, A);
A = multiply(A, A);
n /= 2;
}
return result;
}
long long fibonacci(long long n) {
if (n == 0) return 0;
matrix F = {{1, 1}, {1, 0}};
matrix result = power(F, n - 1);
return result[0][0];
}
int main() {
long long n;
cout << "Enter n: ";
cin >> n;
cout << "Fibonacci(" << n << ") = " << fibonacci(n) << endl;
return 0;
}
以上代码利用矩阵快速幂算法,高效计算了斐波那契数列的第 nnn 项,时间复杂度为 O(logn)O(\log n)O(logn)。
通过了解和掌握常系数齐次线性递推的求解方法和代码实现,可以有效解决许多递推关系问题,从而在竞赛中取得更好的成绩。
问题

前置知识
- 多项式取模
做法
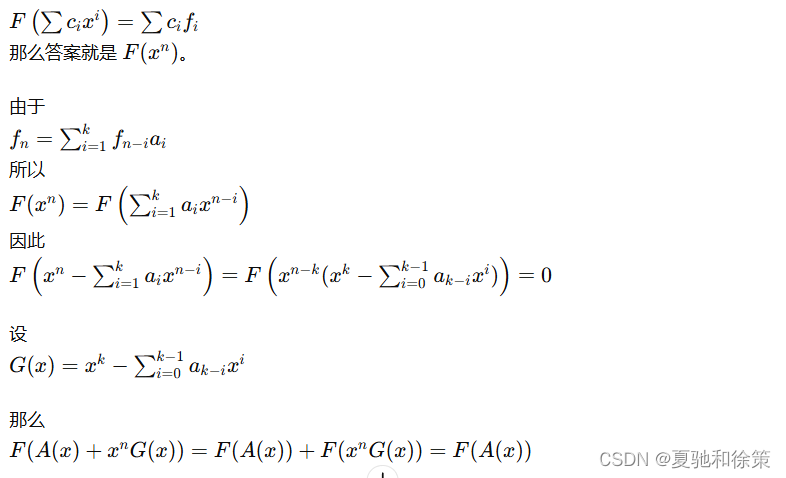
那么就可以通过多次对 A(x)A(x)A(x) 加上 xnG(x)x^n G(x)xnG(x) 的倍数来降低 A(x)A(x)A(x) 的次数。
也就是求 F(A(x)mod G(x))F(A(x) \mod G(x))F(A(x)modG(x)) 其中 A(x)mod G(x)A(x) \mod G(x)A(x)modG(x) 的次数不超过 k−1k-1k−1,而 f0..k−1f_{0..k-1}f0..k−1 已经给出了,就可以计算了。
问题转化成了快速地求 xnmod G(x)x^n \mod G(x)xnmodG(x),只要将普通快速幂中的乘法与取模换成多项式乘法与多项式取模,就可以在 O(klogklogn)O(k \log k \log n)O(klogklogn) 的时间复杂度内解决这个问题了。
矩阵的解释
该算法由 Fiduccia 在 1985 年提出,对于 t≥0t \geq 0t≥0 我们定义列向量 vtv_tvt 为

那么不难发现
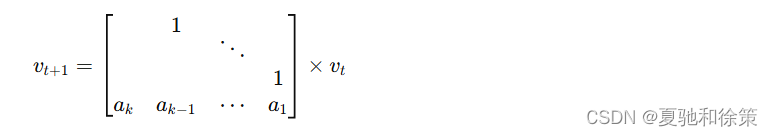
因为 vt+kv_{t+k}vt+k 中每一行都满足这个递推关系,我们将 vt+kv_{t+k}vt+k 描述为一个线性组合如

有

发现若能将两边的 vtv_tvt 消去后得到多项式 ![]()
假设我们要求 MnM^nMn 可以构造多项式 f(x)=xnf(x) = x^nf(x)=xn 那么 f(M)=Mnf(M) = M^nf(M)=Mn,而现在我们可将 f(x)f(x)f(x) 写成 f(x)=Q(x)Γ(x)+R(x)f(x) = Q(x) \Gamma(x) + R(x)f(x)=Q(x)Γ(x)+R(x),而其中零矩阵是没有贡献的,那么 f(M)=R(M)f(M) = R(M)f(M)=R(M)。
但是注意矩阵乘法不满足消去律,此处我们定义矩阵 MMM 的特征多项式为 Γ(x)=det(xI−M)\Gamma(x) = \det(xI - M)Γ(x)=det(xI−M),其中 III 为一个 k×kk \times kk×k 的单位矩阵。Cayley–Hamilton 定理指出 Γ(M)=O\Gamma(M) = OΓ(M)=O,我们观察 MMM 的形式较为特殊,为下 Hessenberg 矩阵,其特征多项式比起一般矩阵更容易计算。
我们从右下角的 2×22 \times 22×2 矩阵开始计算特征多项式

右下角 3×33 \times 33×3 矩阵按照第一行的余子式展开有
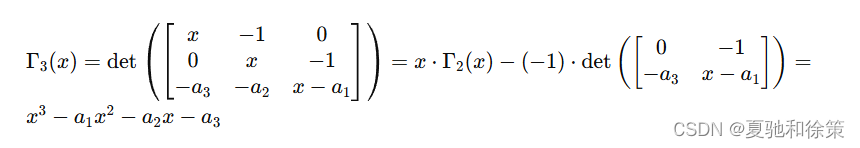
观察并归纳有

至此我们可以使用上面的结论。令 g(x)=f(x)mod Γ(x)g(x) = f(x) \mod{\Gamma(x)}g(x)=f(x)modΓ(x) 有 g(M)=Mng(M) = M^ng(M)=Mn,而 deg(g(x))<k\deg(g(x)) < kdeg(g(x))<k 显然,令

那么

即

我们关注 v0,v1,…,vk−1v_0, v_1, \dots, v_{k-1}v0,v1,…,vk−1 的第一行就是 f0,f1,…,fk−1f_0, f_1, \dots, f_{k-1}f0,f1,…,fk−1 已知,那么 fnf_nfn 可在 O(k)O(k)O(k) 时间简单得到。求出 g(x)g(x)g(x) 则可用快速幂和多项式取模与上述解释是一样的。该算法常数较大,使用生成函数可以得到一个常数更小的算法。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










