10.2 二重积分计算法

最新推荐文章于 2024-08-16 12:18:08 发布

夏驰和徐策

最新推荐文章于 2024-08-16 12:18:08 发布

阅读量2k

点赞数 14

分类专栏：程序猿数学之高等数学文章标签：高等数学

本文链接：https://blog.csdn.net/tang7mj/article/details/139547532

版权

程序猿数学之高等数学专栏收录该内容

80 篇文章

订阅专栏

10.2 二重积分计算法

一、利用直角坐标计算二重积分

在讨论二重积分的计算问题时，我们假定 f(x,y)≥0f(x, y) \ge 0f(x,y)≥0。设积分区域 DDD 可以用不等式来表示：

如图 10-4 所示，其中函数 φ1(x)\varphi_1(x)φ1(x) 和 φ2(x)\varphi_2(x)φ2(x) 在区间 [a,b][a, b][a,b] 上连续。

图 10-4

按照二重积分的几何意义，二重积分的值等于以 DDD 为底，以曲面 z=f(x,y)z = f(x, y)z=f(x,y) 为顶的曲顶柱体的体积。我们可以应用第六章中计算“平行截面面积为已知的立体的体积”的方法来计算这个曲顶柱体的体积。

计算截面面积

图 10-5

一般地，过区间 [a,b][a, b][a,b] 上任一点 xxx 且平行于 y0zy0zy0z 面的平面截曲顶柱体所得截面的面积为：

于是，应用计算平行截面面积为已知的立体体积的方法，得曲顶柱体体积为：

这个体积也就是所求二重积分的值，从而有等式：

上式右端的积分叫做先对 yyy，后对 xxx 的二次积分。就是说，先把 xxx 看做常数，把 f(x,y)f(x, y)f(x,y) 只看做 yyy 的函数，并对 yyy 计算从 φ1(x)\varphi_1(x)φ1(x) 到 φ2(x)\varphi_2(x)φ2(x) 的定积分；然后把算得的结果（是 xxx 的函数）再对 xxx 计算在区间 [a,b][a, b][a,b] 上的定积分。这个先对 yyy，后对 xxx 的二次积分也常记作：

因此，等式也可以写成：

这就是把二重积分化为先对 yyy，后对 xxx 的二次积分的公式。在上述讨论中，我们假定 f(x,y)≥0f(x, y) \ge 0f(x,y)≥0，但实际上公式的成立并不受此条件限制。

类似地，如果积分区域 DDD 可以用不等式表示：

如图 10-6 所示，其中函数 ψ1(y)\psi_1(y)ψ1(y) 和 ψ2(y)\psi_2(y)ψ2(y) 在区间 [c,d][c, d][c,d] 上连续，那么就有：

图 10-6

上式右端的积分叫做先对 xxx，后对 yyy 的二次积分，这个积分也常记作：

因此，等式也可以写成：

这就是把二重积分化为先对 xxx，后对 yyy 的二次积分的公式。

以后我们称图 10-4 所示的积分区域为 X 型区域，图 10-6 所示的积分区域为 Y 型区域。应用公式时，积分区域必须是 X 型区域。 X 型区域 DDD 的特点是：穿过 DDD 内部且平行于 yyy 轴的直线与 DDD 的边界相交不多于两点；而用公式时，积分区域必须是 Y 型区域。 Y 型区域 DDD 的特点是：穿过 DDD 内部且平行于 xxx 轴的直线与 DDD 的边界相交不多于两点。

如果积分区域 DDD 如图 10-7 那样，既有一部分使穿过 DDD 内部且平行于 yyy 轴的直线与 DDD 的边界相交多于两点，又有一部分使穿过 DDD 内部且平行于 xxx 轴的直线与 DDD 的边界相交多于两点，那么 DDD 既不是 X 型区域，又不是 Y 型区域。对于这种情形，可以把 DDD 分成几部分，使每个部分是 X 型区域或是 Y 型区域。例如，在图 10-7 中，把 DDD 分成三部分，它们都是 X 型区域，从而在这三部分上的二重积分都可应用公式。各部分上的二重积分求得后，根据二重积分的性质，它们的和就是在 DDD 上的二重积分。

图 10-7 和图 10-8

将二重积分化为二次积分时，确定积分限是一个关键。积分限是根据积分区域 DDD 来确定的，先画出积分区域 DDD 的图形。假如积分区域 DDD 是 X 型的，如图 10-8 所示，在区间 [a,b][a, b][a,b] 上任意取定一个 xxx 值，积分区域上以这个 xxx 值为横坐标的点在一段直线上，这段直线平行于 yyy 轴，该线段上点的纵坐标从 φ1(x)\varphi_1(x)φ1(x) 变到 φ2(x)\varphi_2(x)φ2(x)，这就是公式中先把 xxx 看做常量而对 yyy 积分时的下限和上限。因为上面的 xxx 值是在 [a,b][a, b][a,b] 上任意取定的，所以再把 xxx 看做变量而对 xxx 积分时，积分区间就是 [a,b][a, b][a,b]。

总结

通过将二重积分化为两次单积分，我们可以更方便地计算复杂区域和函数的积分值。上述方法展示了如何利用直角坐标来处理二重积分问题，并且说明了不同类型区域的处理方法。

例题讲解

图 10-10 和图 10-11 分别显示了用两种方法计算该积分。

解法一

先画出积分区域 DDD（如图 10-10 所示）。DDD 是 XXX 型的，DDD 上的点的横坐标的变动范围是区间 [1,2][1, 2][1,2]。在区间 [1,2][1, 2][1,2] 上任意取定一个 xxx 值，则 DDD 上以这个 xxx 值为横坐标的点在一段直线上，这段直线平行于 yyy 轴，该线段上点的纵坐标从 y=1y = 1y=1 变到 y=xy = xy=x。利用公式 (2-1) 得：

解法二

如图 10-11 所示，积分区域 DDD 是 YYY 型的，DDD 上的点的纵坐标的变动范围是区间 [1,2][1, 2][1,2]。在区间 [1,2][1, 2][1,2] 上任意取定一个 yyy 值，则 DDD 上以这个 yyy 值为纵坐标的点在一段直线上，这段直线平行于 xxx 轴，该线段上点的横坐标从 x=yx = yx=y 变到 x=2x = 2x=2。于是，利用公式 (2-2) 得：

例 2 计算 ∬Dy1+x2−y2 dσ\iint_D y \sqrt{1 + x^2 - y^2} \, d\sigma∬Dy1+x2−y2dσ，其中 DDD 是由直线 y=xy = xy=x， x=−1x = -1x=−1 和 y=1y = 1y=1 所围成的闭区域。

如图 10-12 所示，积分区域 DDD 既是 XXX 型的，又是 YYY 型的。

若利用公式 (2-1)，得：

若利用公式 (2-2)（图 10-13），就有：

其中关于 xxx 的积分计算比较麻烦。所以这里用公式 (2-1) 计算较为方便。

例 3 计算 ∬Dxy dσ\iint_D xy \, d\sigma∬Dxydσ，其中 DDD 是由抛物线 y2=xy^2 = xy2=x 及直线 y=x−2y = x - 2y=x−2 所围成的闭区域。

画出积分区域 DDD 如图 10-14 所示。DDD 既是 XXX 型的，又是 YYY 型的。若利用公式 (2-2)，则得：

若利用公式 (2-1) 来计算，由于在区间 [0,1][0, 1][0,1] 及 [1,4][1, 4][1,4] 上表示 φ1(x)\varphi_1(x)φ1(x) 的式子不同，所以要用经过交点 (1,−1)(1, -1)(1,−1) 且平行于 yyy 轴的直线 x=1x = 1x=1 把区域 DDD 分成 D1D_1D1 和 D2D_2D2 两部分（图 10-15），其中：

因此，根据二重积分的性质 2，就有：

由此可见，这里用公式 (2-1) 来计算需要化为两个二次积分。上述几个例子说明，在化二重积分为二次积分时，为了计算简便，需要选择恰当的二次积分的次序。这时，既要考虑积分区域 DDD 的形状，又要考虑被积函数 f(x,y)f(x, y)f(x,y) 的特性。

例 4 求两个底圆半径都等于 RRR 的直交圆柱面所围成的立体的体积。

解：设这两个圆柱面的方程分别为 x2+y2=R2x^2 + y^2 = R^2x2+y2=R2 及 x2+z2=R2x^2 + z^2 = R^2x2+z2=R2。利用立体关于坐标平面的对称性，只要算出它在第一象限部分（图 10-16(a)）的体积 V1V_1V1，然后再乘 8 就行了。所求立体在第一象限部分可以看成是一个曲顶柱体，它的底为：

如图 10-16(b) 所示，它的顶是柱面于是：

利用公式 (2-1)，得：

从而所求立体的体积为：

总结

通过上述例题的讲解，我们可以看到，化二重积分为二次积分的方法在实际应用中是非常有效的。选择合适的积分次序以及将积分区域进行合理的划分，可以大大简化计算过程，准确地求出二重积分的值。

二、利用极坐标计算二重积分

在某些情况下，积分区域 DDD 的边界曲线用极坐标方程来表示比较方便，同时被积函数用极坐标变量 rrr 和 θ\thetaθ 表达也比较简单。这时，可以考虑利用极坐标来计算二重积分。

二重积分的定义

按二重积分的定义：

假定从极点 OOO 出发且穿过闭区域 DDD 内部的射线与 DDD 的边界曲线相交不多于两点。可以用以极点为中心的一族同心圆：r=常数r = \text{常数}r=常数以及从极点出发的一族射线：θ=常数\theta = \text{常数}θ=常数，将 DDD 分成若干个小闭区域。除了包含边界点的一些小区域外，小闭区域的面积 Δσi\Delta \sigma_iΔσi 可计算如下：

在这些小闭区域内取圆周 r=rir = r_ir=ri 上的一点 (ri,θi)(r_i, \theta_i)(ri,θi)，该点的直角坐标为 (ricos⁡θi,risin⁡θi)(r_i \cos \theta_i, r_i \sin \theta_i)(ricosθi,risinθi)，则有：

于是：

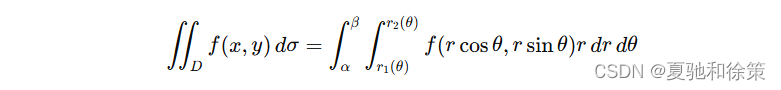
例题讲解

例 5 计算 ∬De−x2−y2 dA\iint_D e^{-x^2 - y^2} \, dA∬De−x2−y2dA，其中 DDD 是由圆心在原点、半径为 aaa 的圆周所围成的闭区域。

在极坐标系中，闭区域 DDD 可表示为：

由公式：

计算如下：

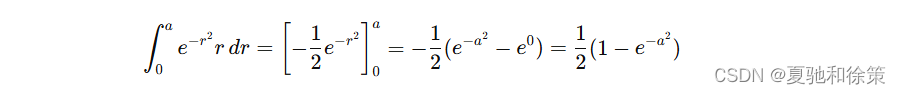
于是：

例 6 求球体 x2+y2+z2≤4a2x^2 + y^2 + z^2 \le 4a^2x2+y2+z2≤4a2 被圆柱面 x2+y2=2axx^2 + y^2 = 2axx2+y2=2ax 所截得的（含在圆柱面内的部分）立体的体积。

如图 10-23 所示：

在极坐标系中，闭区域 DDD 可用不等式表示：

于是体积 VVV 为：

计算如下：

通过变换 r=2acos⁡θsin⁡ϕr = 2a \cos \theta \sin \phir=2acosθsinϕ，有 dr=2acos⁡θcos⁡ϕ dϕdr = 2a \cos \theta \cos \phi \, d\phidr=2acosθcosϕdϕ，积分简化为：

最后化简得到：

这些例题展示了如何利用极坐标变换简化积分计算过程，并得到准确的结果。

三、二重积分的换元法

二重积分的换元法是一种重要的积分技巧，通过适当的变量变换，可以将复杂的积分区域和被积函数转换为更易处理的形式。下面将通过一些例题展示如何应用换元法计算二重积分。

解：

确定变量变换：
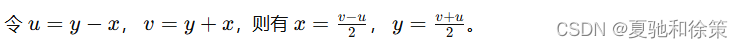
计算雅可比式：变换的雅可比式为：

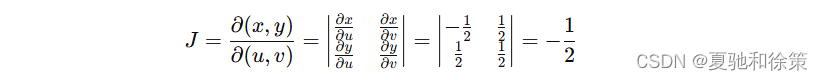
变换后的积分区域：在 u,vu, vu,v 平面上，积分区域 D′D'D′ 的边界由 u=0u = 0u=0、v=2v = 2v=2、u=vu = vu=v 及 u=−vu = -vu=−v 围成。
应用换元公式：

计算积分：

总结

通过换元法，我们可以将复杂的积分区域和被积函数转换为更易处理的形式，利用雅可比式进行变量变换，从而简化计算过程。这一技巧在解决二重积分问题中非常实用。

解：

确定变量变换：令 u=x+yu = x + yu=x+y，v=yxv = \frac{y}{x}v=xy，则有 x=u1+vx = \frac{u}{1 + v}x=1+vu， y=uv1+vy = \frac{uv}{1 + v}y=1+vuv。
计算雅可比式：变换的雅可比式为：

变换后的积分区域：在 u,vu, vu,v 平面上，积分区域 D′D'D′ 的边界由 u=cu = cu=c、u=du = du=d、v=av = av=a、v=bv = bv=b 围成。
应用换元公式：

计算积分：

计算 uuu 的积分：

接着计算 vvv 的积分：

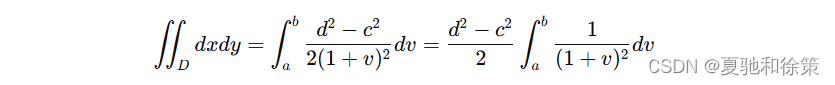
最终结果为：

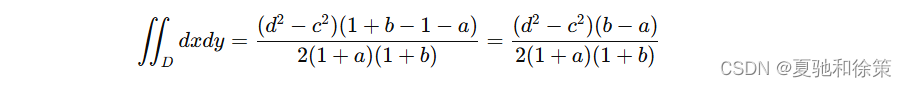
总结

图解

图 10-26(a) 和 图 10-26(b) 分别表示了积分区域 DDD 和 D′D'D′ 的边界：

图 10-26(a)：在 xOyxOyxOy 平面上的积分区域 DDD，由直线 x+y=cx + y = cx+y=c、x+y=dx + y = dx+y=d、y=axy = axy=ax 和 y=bxy = bxy=bx 围成。

图 10-26(b)：在 uOvuOvuOv 平面上的积分区域 D′D'D′，由直线 u=cu = cu=c、u=du = du=d、v=av = av=a 和 v=bv = bv=b 围成。

解：

确定变量变换：令 x=arcos⁡θx = a r \cos \thetax=arcosθ，y=brsin⁡θy = b r \sin \thetay=brsinθ，则有 0≤r≤10 \le r \le 10≤r≤1，0≤θ≤2π0 \le \theta \le 2\pi0≤θ≤2π。
计算雅可比式：变换的雅可比式为：