8.14.9 ACM-ICPC 组合数学 贝尔数

8.14.9 ACM-ICPC 组合数学 贝尔数

引言

在组合数学中，贝尔数（Bell Numbers）是一个非常重要的概念，用于计算集合的非空划分数。在ACM-ICPC竞赛中，贝尔数也是常见的考点之一。本节将详细介绍贝尔数的定义、性质以及计算方法，并通过示例来加深对贝尔数的理解。

贝尔数的定义

贝尔数 BnB_nBn​ 表示将一个包含 nnn 个元素的集合划分为若干个非空子集的不同方式的数量。例如，贝尔数 B3B_3B3​ 表示将包含3个元素的集合划分为不同非空子集的方式数。

贝尔数的性质

贝尔数具有以下几个重要性质：

1. 递推关系：贝尔数可以通过以下递推关系计算： Bn+1=∑k=0n(nk)BkB_{n+1} = \sum_{k=0}^{n} \binom{n}{k} B_kBn+1​=∑k=0n​(kn​)Bk​ 其中， (nk)\binom{n}{k}(kn​) 是二项式系数，表示从 nnn 个元素中选择 kkk 个元素的组合数。

2. 贝尔三角形：贝尔数可以通过贝尔三角形计算，贝尔三角形类似于帕斯卡三角形，其构建规则如下：

   • 第一行只有一个元素， T(0,0)=1T(0, 0) = 1T(0,0)=1。
   • 从第二行开始，每一行的第一个元素等于上一行的最后一个元素。
   • 从第二个元素开始，每一个元素等于该行前一个元素加上上一行对应位置的元素。
   • 第 nnn 行的第一个元素就是贝尔数 BnB_nBn​。

贝尔数的计算方法

递推计算

利用递推关系计算贝尔数的Python代码如下：

def bell_number(n):
    bell = [[0 for i in range(n+1)] for j in range(n+1)]
    bell[0][0] = 1
    
    for i in range(1, n+1):
        bell[i][0] = bell[i-1][i-1]
        for j in range(1, i+1):
            bell[i][j] = bell[i-1][j-1] + bell[i][j-1]
    
    return bell[n][0]

# 计算前10个贝尔数
for i in range(10):
    print(f"B_{i} = {bell_number(i)}")

贝尔三角形

构建贝尔三角形并计算贝尔数的Python代码如下：

def bell_triangle(n):
    triangle = [[0 for _ in range(n+1)] for _ in range(n+1)]
    triangle[0][0] = 1
    
    for i in range(1, n+1):
        triangle[i][0] = triangle[i-1][i-1]
        for j in range(1, i+1):
            triangle[i][j] = triangle[i-1][j-1] + triangle[i][j-1]
    
    return [triangle[i][0] for i in range(n+1)]

# 构建前10行的贝尔三角形
bell_nums = bell_triangle(10)
for i, num in enumerate(bell_nums):
    print(f"B_{i} = {num}")

示例

假设我们要计算前五个贝尔数，我们可以利用上述递推关系或贝尔三角形来进行计算。通过代码，我们可以得到以下结果：

• B0=1B_0 = 1B0​=1
• B1=1B_1 = 1B1​=1
• B2=2B_2 = 2B2​=2
• B3=5B_3 = 5B3​=5
• B4=15B_4 = 15B4​=15

这些贝尔数表示了分别包含0到4个元素的集合的不同划分方式数。

结论

贝尔数在组合数学中有着广泛的应用，对于理解集合划分问题具有重要意义。通过递推关系和贝尔三角形，我们可以有效地计算贝尔数。在ACM-ICPC竞赛中，掌握贝尔数的概念和计算方法将有助于解决相关问题。希望本节内容能够帮助你更好地理解和应用贝尔数。

---

引言

贝尔数（Bell Numbers）是一组在组合数学中具有重要意义的整数数列，命名为埃里克·坦普尔·贝尔（Eric Temple Bell）。贝尔数用于计算一个集合的不同划分方式的数量。贝尔数在ACM-ICPC竞赛中也是常见的考点之一。

贝尔数的定义

贝尔数 BnB_nBn​ 表示基数为 nnn 的集合的划分方法的数目。一个集合 SSS 的划分是将 SSS 分割成若干个两两不相交的非空子集。例如，对于 B3=5B_3 = 5B3​=5，表示含有3个元素的集合 {a, b, c} 有5种不同的划分方法：

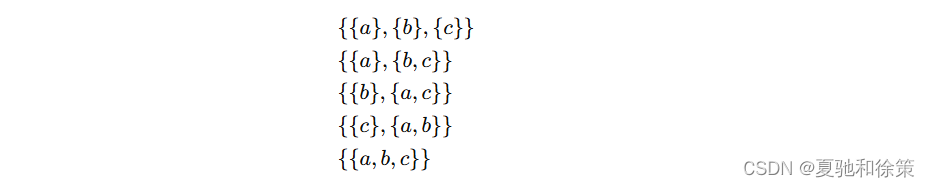
贝尔数从 B0B_0B0​ 开始，空集正好有一种划分方法，因此 B0=1B_0 = 1B0​=1。

贝尔数的递推公式

贝尔数可以通过以下递推公式计算：

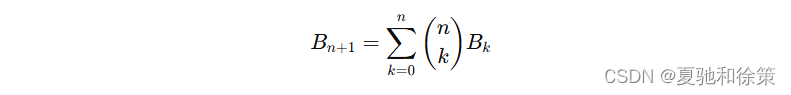
其中， (nk)\binom{n}{k}(kn​) 是二项式系数，表示从 nnn 个元素中选择 kkk 个元素的组合数。

递推公式的证明

设 BnB_nBn​ 为含有 nnn 个元素的集合的划分个数。设集合为 {b_1, b_2, b_3, ..., b_n}，则 Bn+1B_{n+1}Bn+1​ 为含有 n+1n+1n+1 个元素的集合 {b_1, b_2, b_3, ..., b_n, b_{n+1}} 的划分数。

考虑元素 bn+1b_{n+1}bn+1​：

• 

以此类推，我们得到递推公式。

贝尔数与第二类斯特林数的关系

每个贝尔数都是相应的第二类斯特林数的和：

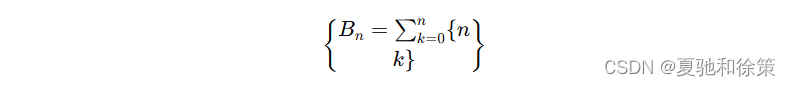
第二类斯特林数 {{nk}}\{n \brace k\}{k}{n​} 表示将基数为 nnn 的集合划分为正好 kkk 个非空子集的方法数目。

贝尔三角形

贝尔三角形类似于杨辉三角形，可以用于递推求出贝尔数。构造贝尔三角形的方法如下：

• 第一行首项为1，即 a0,0=1a_{0,0} = 1a0,0​=1。
• 对于 n≥1n \ge 1n≥1，第 nnn 行首项等于上一行的末项，即 an,0=an−1,n−1a_{n,0} = a_{n-1,n-1}an,0​=an−1,n−1​。
• 对于 m,n≥1m, n \ge 1m,n≥1，第 nnn 行第 mmm 项等于左边和左上角两个数之和，即 an,m=an,m−1+an−1,m−1a_{n,m} = a_{n,m-1} + a_{n-1,m-1}an,m​=an,m−1​+an−1,m−1​。

部分结果如下：

每行的首项是贝尔数。可以利用这个三角形来递推求出贝尔数。

贝尔数的指数生成函数

贝尔数的指数生成函数及其导函数如下：

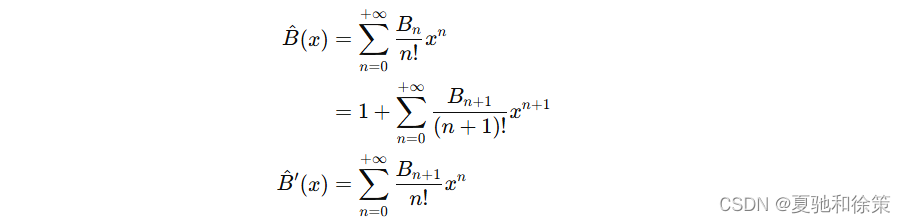
根据贝尔数的递推公式，可以得到：

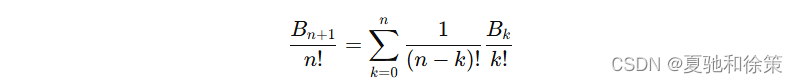
这是一个卷积的式子，因此有：

这是一个微分方程，解得：

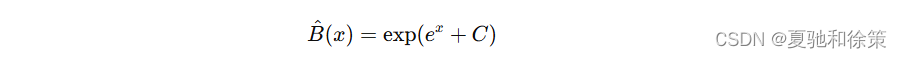
当 x=0x = 0x=0 时，B^(0)=1\hat{B}(0) = 1B^(0)=1，带入后解得 C=−1C = -1C=−1，得到贝尔数指数生成函数的封闭形式：

实现贝尔数的计算

使用递推公式的代码

#include <iostream>
#include <vector>

// 使用递推公式计算贝尔数
int bellNumber(int n) {
    std::vector<std::vector<int>> bell(n + 1, std::vector<int>(n + 1, 0));
    bell[0][0] = 1;

    for (int i = 1; i <= n; i++) {
        bell[i][0] = bell[i - 1][i - 1];
        for (int j = 1; j <= i; j++) {
            bell[i][j] = bell[i - 1][j - 1] + bell[i][j - 1];
        }
    }

    return bell[n][0];
}

int main() {
    int n = 10; // 计算前10个贝尔数
    for (int i = 0; i < n; ++i) {
        std::cout << "B_" << i << " = " << bellNumber(i) << std::endl;
    }
    return 0;
}

使用贝尔三角形的代码

#include <iostream>
#include <vector>

// 构建贝尔三角形并计算贝尔数
std::vector<int> bellTriangle(int n) {
    std::vector<std::vector<int>> triangle(n + 1, std::vector<int>(n + 1, 0));
    triangle[0][0] = 1;

    for (int i = 1; i <= n; i++) {
        triangle[i][0] = triangle[i - 1][i - 1];
        for (int j = 1; j <= i; j++) {
            triangle[i][j] = triangle[i - 1][j - 1] + triangle[i][j - 1];
        }
    }

    std::vector<int> bellNumbers;
    for (int i = 0; i <= n; ++i) {
        bellNumbers.push_back(triangle[i][0]);
    }
    return bellNumbers;
}

int main() {
    int n = 10; // 构建前10行的贝尔三角形
    std::vector<int> bellNumbers = bellTriangle(n);
    for (int i = 0; i <= n; ++i) {
        std::cout << "B_" << i << " = " << bellNumbers[i] << std::endl;
    }
    return 0;
}

结论

贝尔数在组合数学中有着广泛的应用，对于理解集合划分问题具有重要意义。通过递推关系和贝尔三角形，我们可以有效地计算贝尔数。在ACM-ICPC竞赛中，掌握贝尔数的概念和计算方法将有助于解决相关问题。希望本节内容能够帮助你更好地理解和应用贝尔数。

参考文献

• 贝尔数 - 维基百科

​​​​​​​