CUDA并行算法系列之FFT快速卷积
卷积定义
在维基百科上,卷积定义为:
离散卷积定义为:
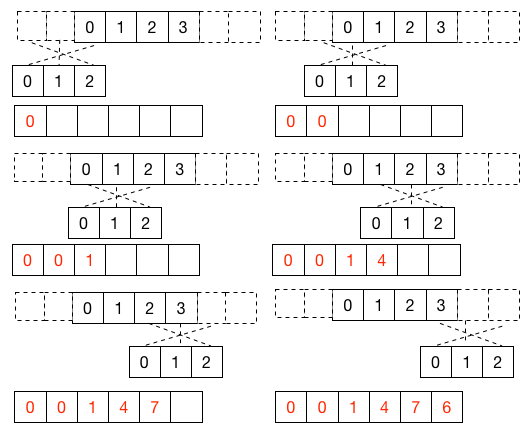
[ 0, 1, 2, 3]和[0, 1, 2]的卷积例子如下图所示:
Python实现(直接卷积)
根据离散卷积的定义,用Python实现:
def conv(a, b):
N = len(a)
M = len(b)
YN = N + M - 1
y = [0.0 for i in range(YN)]
for n in range(YN):
for m in range(M):
if 0 <= n - m and n - m < N:
y[n] += a[n - m] * b[m]
return y把数组b逆序,则可以不交叉计算卷积(使用numpy的array[::-1]即可实现逆序):
import numpy as np
def conv2(a, b):
N = len(a)
M = len(b)
YN = N + M - 1
y = [0.0 for i in range(YN)]
b = np.array(b)[::-1] # 逆序
for n in range(YN):
for m in range(M):
k = n - M + m + 1;
if 0 <= k and k < N:
y[n] += a[k] * b[m]
return y测试
可以利用numpy.convolve来检验计算结果的正确性:
if __name__ == '__main__':
a = [ 0, 1, 2, 3 ]
b = [ 0, 1, 2 ]
print(conv2(a, b))
print(np.convolve(a, b))完整代码可以在Github上找到。
利用FFT快速卷积
时域的卷积和频域的乘法是等价的,同时时域的乘法和频域的卷积也是等价的。基于这个这个前提,可以把待卷积的数组进行FFT变换,在频域做乘法,然后再进行IFFT变换即可得到卷积结果。算法流程描述如下:
- 设
N=len(a),M = len(b), 其中a,b为待卷积的数组,将长度增加到 L>=N+M−1,L=2n,n∈Z ,即








 本文探讨了CUDA并行算法在实现FFT快速卷积中的应用。通过Python代码展示了直接卷积、FFT快速卷积及其CUDA实现,指出FFT卷积在效率上的优势。文章还分析了性能,CUDA直接卷积和cuFFT卷积进一步提升了计算速度。
本文探讨了CUDA并行算法在实现FFT快速卷积中的应用。通过Python代码展示了直接卷积、FFT快速卷积及其CUDA实现,指出FFT卷积在效率上的优势。文章还分析了性能,CUDA直接卷积和cuFFT卷积进一步提升了计算速度。
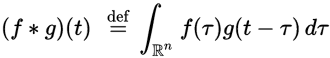
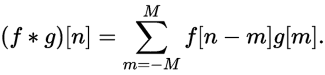
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1132
1132

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








