CUDA并行算法系列之规约
前言
规约是一类并行算法,对传入的N个数据,使用一个二元的符合结合律的操作符⊕,生成1个结果。这类操作包括取最小、取最大、求和、平方和、逻辑与/或、向量点积。规约也是其他高级算法中重要的基础算法。
除非操作符⊕的求解代价极高,否则规约倾向于带宽受限型任务(bandwidthbound)。本文将介绍几种规约算法的实现,从两遍规约、block的线程数必须为2的幂,一步一步优化到单遍规约、任意线程数的规约实现,还将讨论讨论基于C++模板的优化。
规约
对于N个输入数据和操作符+,规约可表示为:
下图展示了一些处理8个元素规约操作的实现:
从图中可以看到,不同的实现其时间复杂度也是不一样的,其中串行实现完成计算需要7步,性能比较差。成对的方式是典型的分治思想,只需要lgN步来计算结果,由于不能合并内存事务,这种实现在CUDA中性能较差。
在CUDA中,无论是对全局内存还是共享内存,基于交替策略效果更好。对于全局内存,使用blockDim.x*gridDim.x的倍数作为交替因子有良好的性能,因为所有的内存事务将被合并。对于共享内存,最好的性能是按照所确定的交错因子来累计部分结果,以避免存储片冲突,并保持线程块的相邻线程处于活跃状态。
两遍规约
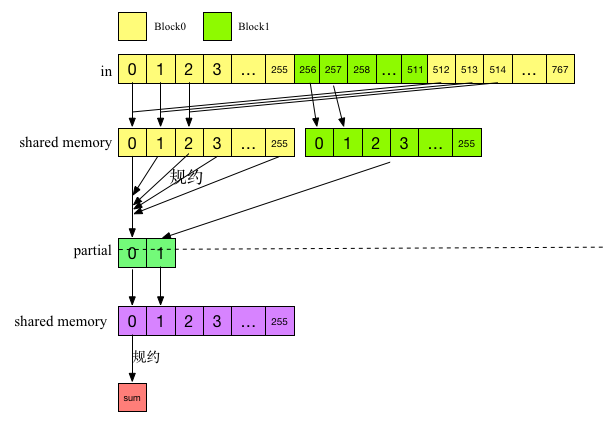
该算法包含两个阶段,并且两个阶段调用同一个内核。第一阶段内核执行NumBlocks个并行规约,其中NumBlocks是指线程块数,得到一个中间结果数组。第二个阶段通过调用一个线程块对这个中间数组进行规约,从而得到最终结果。改算法的执行如下图所示:

假设有对768个输入数据进行规约,NumBlocks=256,第一阶段使用2个Block进行规约,此时内核执行两个并行规约,并把结果保存在中间数组partial中,其中partial的大小为2,partial[0]保存线程块0的规约结果,partial1保存线程块1的结果。第二阶段对parital进行规约,此时内核值启动一个Block,因此,最终得到一个规约结果,这个结果就是对输入数据的规约结果。
规约算法采用了交替策略,两遍规约的代码如下:
// 两遍规约
__global__ void reduction1_kernel(int *out, const int *in, size_t N)
{
// lenght = threads (BlockDim.x)
extern __shared__ int sPartials[];
int sum = 0;
const int tid = threadIdx.x;
for (size_t i = blockIdx.x * blockDim.x + tid; i < N; i += blockDim.x * gridDim.x)
{
sum += in[i];
}
sPartials[tid] = sum;
__syncthreads();
for (int activeTrheads = blockDim.x / 2; activeTrheads > 0; activeTrheads /= 2)
{
if (tid < activeTrheads)
{
sPartials[tid] += sPartials[tid + activeTrheads];
}
__syncthreads();
}
if (tid == 0)
{
out[blockIdx.x] = sPartials[0];
}
}
void reduction1(int *answer, int *partial, const int *in, const size_t N, const int numBlocks, int numThreads)
{
unsigned int sharedSize = numThreads * sizeof(int);
// kernel execution
reduction1_kernel<<<numBlocks, numThreads, sharedSize>>>(partial, in, N);
reduction1_kernel<<<1, numThreads, sharedSize>>>(answer, partial, numBlocks);
}共享内存的大小等于线程块的线程数量,在启动的时候指定。同时要注意,该内核块的线程数量必须是2的幂次,在下文,将介绍如何使用任意大小的数据。
CUDA会把线程组成线程束warp(目前是32个线程),warp的执行由SIMD硬件完成,每个线程块中的线程束是按照锁步方式(lockstep)执行每条指令的,因此当线程块中活动线程数低于硬件线程束的大小时,可以无须再调用__syncthreads()来同步。不过需要注意,编写线程束同步代码时,必须对共享内存的指针使用volatile关键字修饰,否则可能会由于编译器的优化行为改变内存的操作顺序从而使结果不正确。采用线程束优化的代码如下:
// 两遍规约
__global__ void reduction1_kernel(int *out, const int *in, size_t N)
{
// lenght = threads (BlockDim.x)
extern __shared__ int sPartials[];
int sum = 0;
const int tid = threadIdx.x;
for (size_t i = blockIdx.x * blockDim.x + tid; i < N; i += blockDim.x * gridDim.x)
{
sum += in[i];
}
sPartials[tid] = sum;
__syncthreads();
for (int activeTrheads = blockDim.x / 2; activeTrheads > 32; activeTrheads /= 2)
{
if (tid < activeTrheads)
{
sPartials[tid] += sPartials[tid + activeTrheads];
}
__syncthreads();
}
// 线程束同步
if (tid < 32)
{
volatile int *wsSum = sPartials;
if (blockDim.x > 32)
{
wsSum[tid] += wsSum[tid + 32];
}
wsSum[tid] += wsSum[tid + 16];
wsSum[tid] += wsSum[tid + 8];
wsSum[tid] += wsSum[tid + 4];
wsSum[tid] += wsSum[tid + 2];
wsSum[tid] += wsSum[tid + 1];
if (tid == 0)
{
out[blockIdx.x] = wsSum[0];
}
}
}通过把线程数变成一个模板参数,还可以把for循环展开进一步优化,展开后的代码如下:
// 两遍规约
template<unsigned int numThreads>
__global__ void reduction1_kernel(int *out, const int *in, size_t N)
{
// lenght = threads (BlockDim.x)
extern __shared__ int sPartials[];
int sum = 0;
const int tid = threadIdx.x;
for (size_t i = blockIdx.x * numThreads+ tid; i < N; i += numThreads * gridDim.x)
{
sum += in[i];
}
sPartials[tid] = sum;
__syncthreads();
if (numThreads >= 1024)
{
if (tid < 512) sPartials[tid] += sPartials[tid + 512];
__syncthreads();
}








 本文详细探讨了CUDA中的规约算法,包括两遍规约、基于原子操作和非原子操作的单遍规约,以及如何适应任意线程块大小。通过测试对比,展示了不同规约算法在不同GPU上的性能表现,并提供了完整代码供参考。
本文详细探讨了CUDA中的规约算法,包括两遍规约、基于原子操作和非原子操作的单遍规约,以及如何适应任意线程块大小。通过测试对比,展示了不同规约算法在不同GPU上的性能表现,并提供了完整代码供参考。
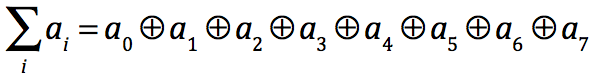
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1295
1295

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








