白话经典算法系列之七堆与堆排序（改）

最新推荐文章于 2023-05-27 00:17:40 发布

不想学编程

最新推荐文章于 2023-05-27 00:17:40 发布

阅读量672

点赞数 1

分类专栏：数据结构文章标签：数据结构堆排序排序算法

数据结构专栏收录该内容

11 篇文章 0 订阅

订阅专栏

转载地址：原帖地址

堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。学习堆排序前，先讲解下什么是数据结构中的二叉堆。

二叉堆的定义

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

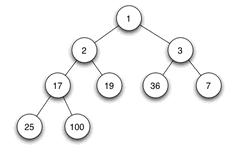
由于其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。

堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

堆的操作——插入删除

下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解，再给出本人的实现代码，最好是先看明白图后再去看代码。

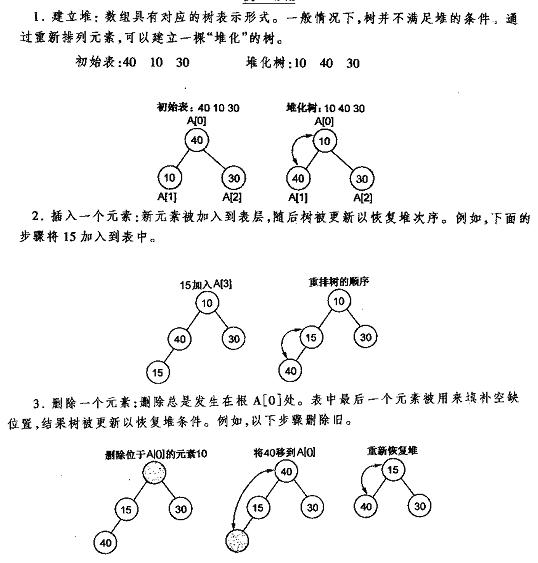
注意：堆就是优先队列，队列的插入操作都是在队尾进行，删除操作都是在队头进行，不过删除操作需要把最后一个元素补到队列头，这样可以保持二叉堆的结构。

堆的插入

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中，对照《白话经典算法系列之二直接插入排序的三种实现》不难写出插入一个新数据时堆的调整代码：

上滤步骤：

[cpp]view plaincopy 
   
 //  新加入i结点  其父结点为(i - 1) / 2  
 void MinHeapFixup(int a[], int i)  
 {  
     int j, temp;  
       
     temp = a[i];  
     j = (i - 1) / 2;      //父结点  
     while (j >= 0 && i != 0)  
     {  
         if (a[j] <= temp)  
             break;  
           
         a[i] = a[j];     //把较大的子结点往下移动,替换它的子结点  
         i = j;  
         j = (i - 1) / 2;  
     }  
     a[i] = temp;  
 }  

插入操作（堆尾操作）：

[cpp]view plaincopy 
   
 //在最小堆中加入新的数据nNum  
 void MinHeapAddNumber(int a[], int n, int nNum)  
 {  
     a[n] = nNum;  
     MinHeapFixup(a, n);  
 }  

堆的删除

按定义，堆中每次都只能删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码：

下滤步骤：

[cpp]view plaincopy 
   
 //  从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2  
 void MinHeapFixdown(int a[], int i, int n)  
 {  
     int j, temp;  
   
     temp = a[i];  
     j = 2 * i + 1;  
     while (j < n)  
     {  
         if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的  
             j++;  
   
         if (a[j] >= temp)  
             break;  
   
         a[i] = a[j];     //把较小的子结点往上移动,替换它的父结点  
         i = j;  
         j = 2 * i + 1;  
     }  
     a[i] = temp;  
 }  

删除操作(堆头操作):

//在最小堆中删除数
void MinHeapDeleteNumber(int a[], int n)
{
Swap(a[0], a[n - 1]);
MinHeapFixdown(a, 0, n - 1);
}

堆化数组

有了堆的插入和删除后，再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧，不用！先看一个数组，如下图：

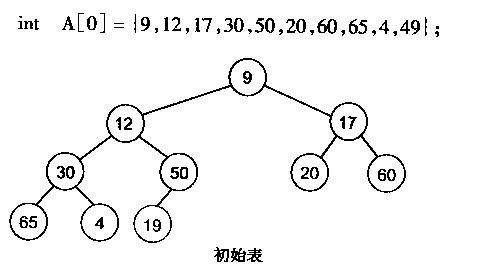
很明显，对叶子结点来说，可以认为它已经是一个合法的堆了即20，60， 65， 4， 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30，A[2] = 17，A[1] = 12，A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤：

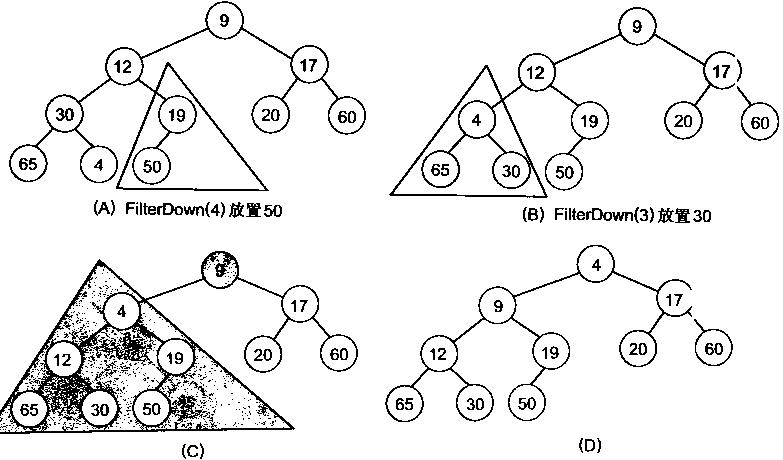
写出堆化数组的代码：

[cpp]view plaincopy 
   
 //建立最小堆  
 void MakeMinHeap(int a[], int n)  
 {  
     for (int i = n / 2 - 1; i >= 0; i--) 
         MinHeapFixdown(a, i, n);  
 }  

（注：i=n/2-1,除以2是因为只需要下滤时父节点会和叶子节点比较，所有只需要下滤所有非叶子节点。-1是因为c++中数组是从0开始计数）

至此，堆的操作就全部完成了(注1)，再来看下如何用堆这种数据结构来进行排序。

堆排序

首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。

由于堆也是用数组模拟的，故堆化数组后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。有点类似于直接选择排序。

[cpp]view plaincopy 
   
 void MinheapsortTodescendarray(int a[], int n)  
 {  
     for (int i = n - 1; i >= 1; i--)  
     {  
         Swap(a[i], a[0]);  
         MinHeapFixdown(a, 0, i);  
     }  
 }  

注意使用最小堆排序后是递减数组，要得到递增数组，可以使用最大堆。

由于每次重新恢复堆的时间复杂度为O(logN)，共N - 1次重新恢复堆操作，再加上前面建立堆时N / 2次向下调整，每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。

下面自己写的堆排序完整算法：（这里是采用小顶堆，得到的是递减数组，如果想改成大顶堆，修改一下判断条件即可）

注意：堆排序用的是删除节点（下滤操作）、建立堆化数组

#include <iostream>
using namespace std;

void swap( int &a, int &b )
{
	int temp;
	temp = a;
	a = b;
	b = temp;
}

//下滤步骤
void MinHeapFixdown(int a[],int i,int n)
{
	int j,temp;

	temp = a[i];
	j = 2*i + 1;
	while( j<n )
	{
		if( a[j]>a[j+1] && j+1<n )
			j++;
		
		if(  a[j]>=temp )
			break;
		else
		{
			a[i] = a[j];
			i = j;
			j = i*2+1;
		}
	}
	a[i] = temp;
}

//在最小堆中删除数，队列头操作
void MinHeapDeleteNum(int a[], int n)
{
	swap(a[0], a[n-1]);
	MinHeapFixdown(a, 0 ,n-1);
}


//建立堆化数组（下滤所有的非叶子节点，所以是n/2-1，-1是因为数组从0开始计数）
void MakeMinHeap(int a[], int n)
{
	for (int i = n / 2 - 1; i >= 0; i--)
		MinHeapFixdown(a, i, n);
}


//堆排序
void HeapSort(int a[], int n)
{
	for(int i=n-1; i>=1; i--)
	{
		swap( a[i], a[0] );
		MinHeapFixdown(a, 0, i);
	}
}

void main()
{
	int a[7] = {5,3,1,4,2,7,6};

	cout<<"初始数组为： ";
    for(int i=0;i<7;i++)
	{
		cout<<a[i]<<' ';
	}
	cout<<endl;

	MakeMinHeap(a,7);
	cout<<"堆化数组为： ";
	for(int i=0;i<7;i++)
	{
		cout<<a[i]<<' ';
	}
	cout<<endl;

	HeapSort(a,7);
	cout<<"堆排序数组： ";
	for(int i=0;i<7;i++)
	{
		cout<<a[i]<<' ';
	}
	cout<<endl;
}

结果：