一文了解差分进化算法的前世今生

差分进化算法（Differential Evolution，以下简称 DE）由Storn等人于1995年提出，其最初的设想是用于解决切比雪夫多项式问题，后来发现它也可用于求解复杂优化问题。当前，它已经成为求解 连续变量非线性全局优化问题的最有效方法之一。与遗传算法类似，DE是一种基于种群进化的元启发式算法。

PS：博主的博士课题以改进DE为主。研究过程中，走了很多弯路。以下内容，主要为这些年针对DE的相关总结。希望此文可以帮助朋友们降低了解和认识DE的准入门槛，若真如此，幸甚。若有相关问题，欢迎留言或私信讨论。

综合表现

下表列举了2005-2020年IEEE CEC 单目标参数优化竞赛的前三名优化算法。其中，2005年和2016年未针对算法进行总排名，不参与统计（用N/A表示）； 2007年为多目标优化问题，不参与统计（用N/A表示）；2009年和2014 年的第二名和第三名算法，未在网站上公布，表中也未列出（用N/A表示）。

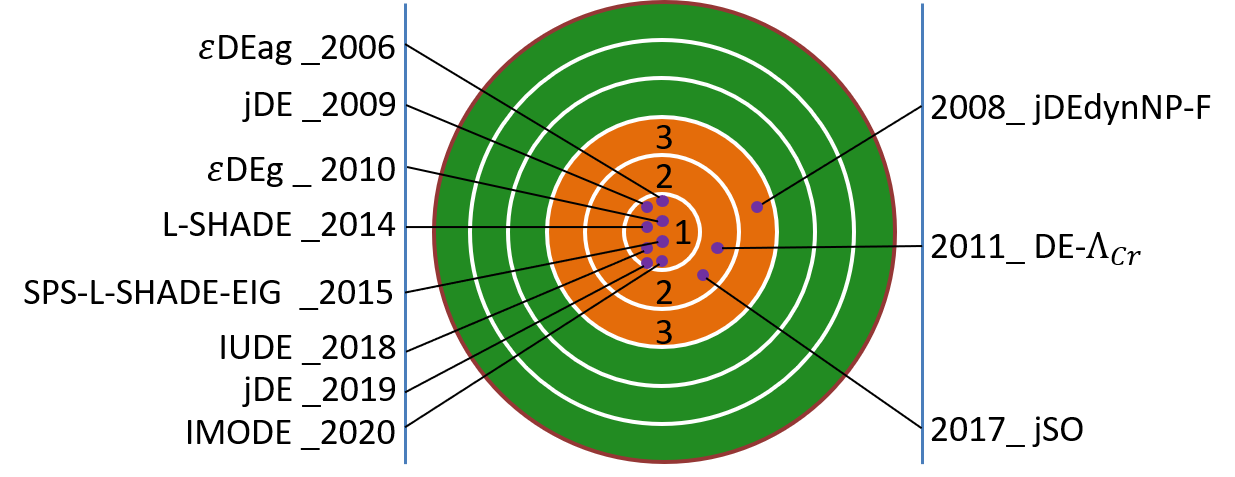
上表中的DE算法和改进DE算法用黑体标注。从表中可以看出，DE在求解标准测试算例时，具有较为明显的优势。下图汇总了DE在各届IEEE CEC竞赛中的最优排名及其对应的改进DE。除了2013年排名第4外（图中未标出），DE在其他所有年份的排名都位列前三。在2006和2009等7个年份中，DE取得了第一名的成绩。在最近三年的竞赛中，即2018年、2019年和2020年，DE依然保持着领先的地位。

流程概述

设定优化问题如下：优化变量为$\mathbf{x}$，变量维度为$D$，表示为
$$\mathbf{x}=\left(x^1,x^2,...,x^D\right)$$
$\mathbf{x}$的上界${\mathbf{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$和下界 ${\mathbf{x}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$分别定义为
$$\{\begin{array}{l}{\mathbf{x}}_{\min }=\left(x_{\min }^1,x_{\min }^2,...,x_{\min }^D\right)\\ {\mathbf{x}}_{\max }=\left(x_{\max }^1,x_{\max }^2,...,x_{\max }^D\right)\end{array}$$
目标函数为最小化某一性能指标
$$\min f\left(\mathbf{x}\right)$$
针对以上的最小化问题，经典DE在求解过程中，一般包含4个步骤：初始化（Initialization）、变异（Mutation）、交叉（Crossover）和选择（Selection）。

初始化

DE的种群可以表示为
$${\mathbf{x}}_i=\left(x_i^1,x_i^2,...,x_i^D\right),i=1,2,...,NP$$
其中，$NP$是种群大小。

初始化第$i$个个体$x_{i,1}$的常用方法为
$$x_{i,1}^j=x_{\min }^j+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(0,1\right)\cdot \left(x_{\max }^j-x_{\min }^j\right),j=1,2,...,D$$
其中，$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}(0,1)$是0~1之间的均匀随机数。

变异

定义${\mathbf{x}}_{i,G}$为第$i$代种群的第$G$个个体。${\mathbf{x}}_{i,G}$通过以下的变异算子生成与之对应的变异向量 ${\mathbf{v}}_{i,G}$
$${\mathbf{v}}_{i,G}={\mathbf{x}}_{r_1^i,G}+F\cdot \left({\mathbf{x}}_{r_2^i,G}-{\mathbf{x}}_{r_3^i,G}\right)$$

其中，下标$r_1^i$、$r_2^i$ 和 $r_3^i$是随机产生的整数值，范围是1~$NP$，它们的数值互不相同，并且均不等于$i$。对于每个变异向量，这些下标都只随机产生一次。此处， ${\mathbf{x}}_{i,G}$被称为${\mathbf{v}}_{i,G}$对应的目标向量，${\mathbf{x}}_{r_1^i,G}$为基向量，${\mathbf{x}}_{r_2^i,G}-{\mathbf{x}}_{r_3^i,G}$是差分向量，$F$是缩放因子，范围是0~1。

交叉

交叉算子如下所示，其作用是通过组合${\mathbf{x}}_{i,G}$和${\mathbf{v}}_{i,G}$产生对应的试验向量${\mathbf{u}}_{i,G}$
$$u_{i,G}^j=\{\begin{array}{l}{v}_{i,G}^j,\text{if}\left(j=j_{\text{rand}}\right)\text{or}\left(r_i^j\le Cr\right)\\ x_{i,G}^j,\text{otherwise}\end{array}$$其中，$j_{\text{rand}}$是1~$D$之间的随机整数，$r_i^j=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}(0,1)$ ，$Cr$是交叉概率，范围是0~1。该方式下，至少存在1维变量从${\mathbf{v}}_{i,G}$到${\mathbf{u}}_{i,G}$。下图为生成试验向量${\mathbf{u}}_{i,G}$的示意图。

选择

生成${\mathbf{u}}_{i,G}$后，计算和比较${\mathbf{u}}_{i,G}$和${\mathbf{x}}_{i,G}$对应的目标函数，目标函数较小的对应向量可以保留到下一代
$${\mathbf{x}}_{i,G+1}=\{\begin{array}{l}{\mathbf{u}}_{i,G},f\left({\mathbf{u}}_{i,G}\right)\le f\left({\mathbf{x}}_{i,G}\right)\\ {\mathbf{x}}_{i,G},\text{otherwise}\end{array}$$

算法特点

相比其他元启发式算法，DE的主要特点在于它使用差分向量来指导当前种群的进化方向。为了直观地展示差分向量（变异向量）的变化特点，本节结合经典DE求解2维Schwefel函数的优化实例，进行详细描述。

下图为2维Schwefel函数的3-D曲面图，其中$x$和 $y$的范围均为-500~500。从图上可知，该函数中除了全局最优解外，还包含数量众多的局部最优解。

接下来，使用刚刚介绍的经典DE进行求解。设置种群大小$NP=30$，缩放因子$F=0.5$，交叉概率$Cr=0.1$。下图记录了不同代数时的变异向量末端点的所有可能位置。在初始化种群后，虽然种群大小$NP$仅为30，但是变异向量几乎可以覆盖所有的搜索空间。此时，个体差异较大， DE可以在较大范围内进行搜索，因此这个阶段的全局探索能力较强；12代时，优化过程逐渐摒弃中心位置，向边界附近搜索；19代时，搜索范围聚集到4个角落；23代时，优化区间已经减至2个小范围；25代时，只剩下一个搜索区域。此时，个体间差异也变小，局部开发能力更强，在40代时，基本收敛。因此，在优化过程中，差分向量可以利用个体差异的变化，自适应地调整DE的全局探索和局部开发能力，从而保证DE具有非常好的综合优化性能。

算法改进

经典DE虽然为求解全局优化问题提供了一种可行的途径，但是它还存在一些不足，比如易陷入局部最优、出现早熟收敛或搜索停滞等现象。为了提升DE的全局优化性能，许多学者致力于改进DE的相关工作。总的来说，改进DE的方法可以分别或同时从以下4个方面入手，包括：变异算子、种群大小$NP$、缩放因子$F$和交叉概率$Cr$。

变异算子

为了区分不同类型的变异算子，一般使用“DE/x/y”对其简述。其中，$x$表示基向量，$y$表示差分向量。经典DE中的变异算子通常被标记为DE/rand/1。此后，学者们又提出了DE/best/1、DE/rand/2、DE/best/2和DE/current-to-$p$best/1等变异算子。当前，DE/current-to-$p$best/1变异算子是各种改进DE的最常用算子之一，其表达式如下
$${\mathbf{v}}_{i,G}={\mathbf{x}}_{i,G}+F_i\left({\mathbf{x}}_{\text{best },G}^p-{\mathbf{x}}_{i,G}\right)+F_i\left({\mathbf{x}}_{r1,G}-{\tilde{\mathbf{x}}}_{r2,G}\right)$$式中，${\mathbf{x}}_{\text{best },G}^p$为第$G$代种群前$NP\ast p$个最好的个体，$p$的范围是0~1 。 ${\mathbf{x}}_{r1,G}$为从1~$NP$范围内随机选取的个体，${\tilde{\mathbf{x}}}_{r2,G}$为从1~$NP$与A（Archive）组成的集合中随机选取的个体，$i$、$r1$和$r2$互不相等。A中保存的是历史迭代过程中目标函数较差的个体。在优化开始阶段，A和第一代的种群相同；此后，逐渐向A中增加目标函数较差个体的数量；当A 中个体数量超过最大值时，将从中随机删除部分个体，并添加进新个体。下图为DE/current-to-$p$best/1变异算子下，生成试验向量的示意图， 差分向量1为${\mathbf{x}}_{\text{best },G}^p-{\mathbf{x}}_{i,G}$，差分向量2为${\mathbf{x}}_{r1,G}-{\tilde{\mathbf{x}}}_{r2,G}$。

种群数量$NP$

种群设置的方式主要包含2种，固定值和自适应方式。在固定值中，通常认为种群数$NP$设置为变量个数5~10倍为宜；2006年，自适应的$NP$设计技术首次被证明有利于提升DE的优化性能，2014年，L-SHADE（DE的改进算法）在IEEE CEC 2014 测试算例上的优化表现排名第一，它更直接地证明了自适应种群设计技术的显著优势。该算法使用的是线性减少种群大小$NP$值的方法。此后陆续又提出了其他的自适应调整$NP$值的方式，如基于小生境（Niching-based）的$NP$减少方法等。

缩放因子$F$和变异率$Cr$

设计缩放因子$F$的方式可以分为四类：固定值、随机值、基于历史自适应和基于目标函数自适应。固定值指的是缩放因子$F$在整个优化过程中，都保持不变。一般认为，$F$取0.5，0.6或0.9为宜。随机值指的是每一代缩放因$F$的值通过随机函数来确定。在研究过程中，均匀分布函数和正态分布函数是最常用的两种方式。

历史自适应缩放因子$F$的核心是借鉴以往迭代成功的缩放因子$F$值，作为设定当前缩放因子$F$值的参考基准。下图(a)给出了历史自适应缩放因子$F$设计的示意图。该方法广泛应用于各种自适应DE算法，SHADE是其中最为典型的算法。目标函数自适应缩放因子$F$是指利用当前种群的目标函数来确定当前的缩放因子$F$。下图 (b)给出了目标函数自适应缩放因子$F$设计的示意图。

交叉概率$Cr$的设计方式与缩放因子$F$类似，本文不再赘述。

改进DE排名

下图依据全局寻优能力的的区别，绘制了25种不同DE算法之间的相互关系 。各类改进DE从下到上，全局寻优能力逐渐提升。每两条红色虚线区间内的DE认为其全局寻优性能类似。DE之间的箭头指向表示来源关系，例如EsDEr-NR是JADEw的改进版。

发展方向

超参数改进

在DE算法中，超参数主要是指缩放因子$F$、交叉概率$Cr$和$NP$。针对$F$和$Cr$的改进策略最近几年以历史自适应为主，如果不能从基本策略上有新的自适应设计，难以再有突破。博主针对该问题曾有部分新的想法，可惜不过限于时间约束，没能仔细研究透彻，略有可惜。

$NP$的改进设计具有通用性，可以用于DE的$NP$自适应方案理论上也可以用于其他智能优化算法。如果能有技术突破，也是非常有价值的。

变异算子改进

DE的核心在于变异算子。不同的变异算子，具有不同的特点。现在还有很多学者去尝试提出新的变异算子。不过更有前途的，博主认为是去融合不同类型的变异算子。IMODE（IEEE CEC 2020冠军）是其中的一个典型代表。相信未来几年，这将成为DE的研究热点之一。

某种意义上，变异算子可以认为是不同智能优化算法融合的另一种体现。举个例子，DE/current-to-$p$best/1的来源之一是粒子群算法。所以，强行想从概念上去融合DE与其他智能优化算法，不如直接去研究融合多个变异算子，更加有意义。

应用范围扩展

针对连续变量非线性全局优化问题，DE当前几乎可以判定为当之无愧的Number 1了。但是在其他问题类型上的综合表现，是否具有统治地位，并不明朗。一个显然的实例，针对组合优化问题，DE的全局搜索能力并不亮眼。大规模优化问题和多目标优化问题是近几年的热点优化问题，DE的表现，就有待各位大佬去探索了。