一、对FFT的介绍
1. FFT(Fast Fourier Transformation),即为快速傅里叶变换,是离散傅里叶变换的快速算法,它是根据离散傅里叶变换的奇、偶、虚、实等特性,对离散傅里叶变换的算法进行改进获得的。
2.FFT算法的基本原理
FFT算法是把长序列的DFT逐次分解为较短序列的DFT。
按照抽取方式的不同可分为DIT-FFT(按时间抽取)和DIF-FFT(按频率抽取)算法。按蝶形运算的构成不同可分为基2,基4,基8,以及任意因子的类型。
3.迭代关系
4、本次程序的基本过程
我们这次所研究的是数字信号处理中的FFT算法,我们这次所用的数字信号是复数类型的。
(1)所以首先,我们先定义了一个复数结构体,因为是进行复数的运算,我们又相继定义复数的加减乘运算的函数。
(2)紧接着,我们定义了进行FFT计算的fft()快速傅里叶变换函数initW() 初始化变换核函数即旋转因子的计算,change() 变址函数,output()输出傅里叶变换的结果的函数。
(3)定义主函数,并调用定义好的相关子函数,利用fft()中的蝶形运算以及change()函数来完成从时间域上选取的DIT-FFT。
二、FFT中码位倒置排序
1、码位倒置的实现方法:
(1)简单的利用按位与、或循环实现
(2)利用公式推导的迭代方法
2、为什么要进行码位倒置
因为由于FFT的计算特性,如果按照正常顺序输入,而没有进行码位倒置的话,就会以乱序输出,就不便于我们后续对信号的相关性质进行研究了,所以DIT-FFT算法就是在进行FFT计算之前,进行分奇偶后的码位倒置运算,即二进制数的倒位。
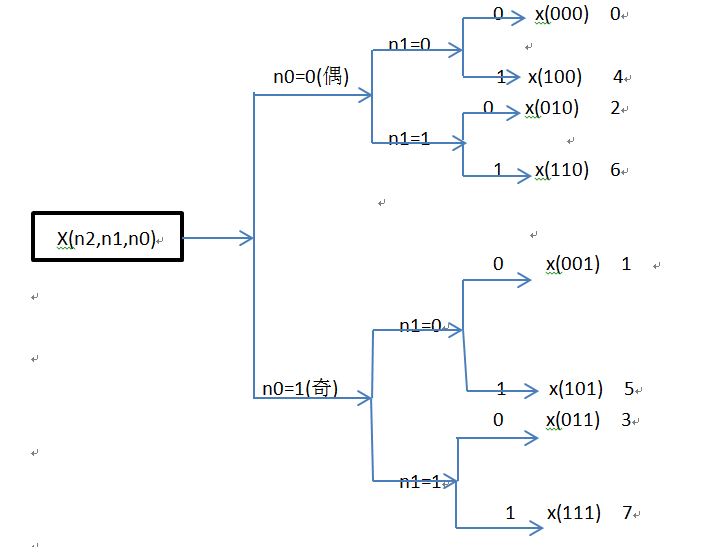
3、倒位序由奇偶分组造成,以N=8为例,说明如下:
三、蝶形运算
由
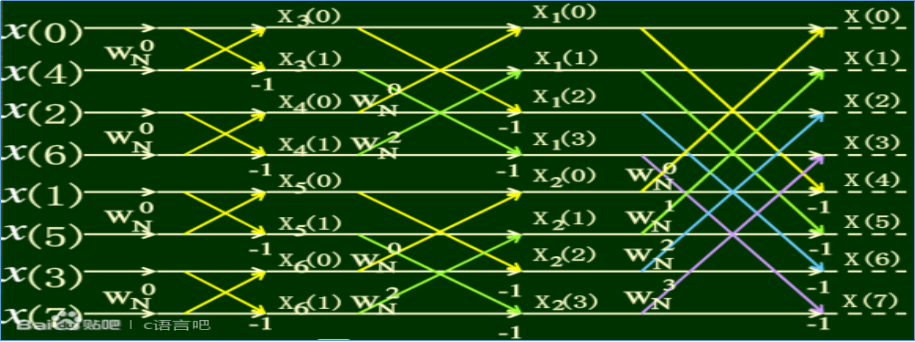
按照上述公式的规律进行逐级分解,直到2点DFT,如下是N=8时的蝶形算法分析图:
四、FFT算法中蝶形算法的基本思想分析
(1)我们知道N点FFT运算可以分成log2(N)级,每一级都有N/2个碟形,FFT的基本思想是用3层循环完成全部运算(N点FFT)。
(2)第一层循环:由于N=2^m需要m级计算,第一层循环对运算的级数进行控制。(stages)
(3)第二层循环:由于第L级有2^(L-1)个蝶形因子(乘数),第二层循环根据乘数进行控制,保证对于每一个蝶形因子第三层循环要执行一次,这样,第三层循环在第二层循环控制下,每一级要进行2^(L-1)次循环计算.(选择W)
(4)第三层循环:由于第L级共有N/2^L即2^(n-L)个群,并且同一级内不同群的乘数分布相同,当第二层循环确定某一乘数后,第三层循环要将本级中每个群中具有这一乘数的蝶形计算一次,即第三层循环每执行完一次要进行N/2^L个碟形计算。(执行不同group中具有相同W的蝶形运算)
(5)可以得出结论:在每一级中,第三层循环完成N/2^L个碟形计算;第二层循环使第三层循环进行 2^(L-1)次,因此,第二层循环完成时,共进行2^(L-1) *N/2^L=N/2个碟形计算。实质是:第二、第三层循环完成了第L级的计算。
五、用c语言实现的FFT算法如下:
<span style="font-size:18px;">#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define N 1000
/*定义复数类型*/
typedef struct{
double real;
double img;
}complex;
complex x[N], *W; /*输入序列,变换核*/
int size_x=0; /*输入序列的大小,在本程序中仅限2的次幂*/
double PI; /*圆周率*/
void fft(); /*快速傅里叶变换*/
void initW(); /*初始化变换核*/
void change(); /*变址*/
void add(complex ,complex ,complex *); /*复数加法*/
void mul(complex ,complex ,complex *); /*复数乘法*/
void sub(complex ,complex ,complex *); /*复数减法*/
void output();/*输出快速傅里叶变换的结果*/
int main()
{
int i; /*输出结果*/
system("cls");
PI=atan(1)*4;
printf(" 输出DIT方法实现的FFT结果\n");
printf("Please input the size of x:\n");//输入序列的大小
scanf("%d",&size_x);
printf("Please input the data in x[N]:\n");//输入序列的实部和虚部
for(i=0;i<size_x;i++)
{
printf("请输入第%d个序列:",i);
scanf("%lf%lf",&x[i].real,&x[i].img);
}
printf("输出倒序后的序列\n");
initW();//调用变换核
fft();//调用快速傅里叶变换
printf("输出FFT后的结果\n");
output();//调用输出傅里叶变换结果函数
return 0;
}
/*快速傅里叶变换*/
void fft()
{
int i=0,j=0,k=0,l=0;
complex up,down,product;
change(); //调用变址函数
for(i=0;i< log(size_x)/log(2) ;i++) /*一级蝶形运算 stage */
{
l=1<<i;
for(j=0;j<size_x;j+= 2*l ) /*一组蝶形运算 group,每个group的蝶形因子乘数不同*/
{
for(k=0;k<l;k++) /*一个蝶形运算 每个group内的蝶形运算*/
{
mul(x[j+k+l],W[size_x*k/2/l],&product);
add(x[j+k],product,&up);
sub(x[j+k],product,&down);
x[j+k]=up;
x[j+k+l]=down;
}
}
}
}
/*初始化变换核,定义一个变换核,相当于旋转因子WAP*/
void initW()
{
int i;
W=(complex *)malloc(sizeof(complex) * size_x); //生成变换核
for(i=0;i<size_x;i++)
{
W[i].real=cos(2*PI/size_x*i); //用欧拉公式计算旋转因子
W[i].img=-1*sin(2*PI/size_x*i);
}
}
/*变址计算,将x(n)码位倒置*/
void change()
{
complex temp;
unsigned short i=0,j=0,k=0;
double t;
for(i=0;i<size_x;i++)
{
k=i;j=0;
t=(log(size_x)/log(2));
while( (t--)>0 ) //利用按位与以及循环实现码位颠倒
{
j=j<<1;
j|=(k & 1);
k=k>>1;
}
if(j>i) //将x(n)的码位互换
{
temp=x[i];
x[i]=x[j];
x[j]=temp;
}
}
output();
}
/*输出傅里叶变换的结果*/
void output()
{
int i;
printf("The result are as follows:\n");
for(i=0;i<size_x;i++)
{
printf("%.4f",x[i].real);
if(x[i].img>=0.0001)printf("+%.4fj\n",x[i].img);
else if(fabs(x[i].img)<0.0001)printf("\n");
else printf("%.4fj\n",x[i].img);
}
}
void add(complex a,complex b,complex *c) //复数加法的定义
{
c->real=a.real+b.real;
c->img=a.img+b.img;
}
void mul(complex a,complex b,complex *c) //复数乘法的定义
{
c->real=a.real*b.real - a.img*b.img;
c->img=a.real*b.img + a.img*b.real;
}
void sub(complex a,complex b,complex *c) //复数减法的定义
{
c->real=a.real-b.real;
c->img=a.img-b.img;
}
</span>
六、FFT原理的理解和程序设计中遇到的相关问题及解决方法
1、遇到的相关问题:
(1)首先一开始不知道什么是FFT,以及FFT原理是什么
(2)不理解FFT中迭代关系的推导以及缘由
(3)不理解变址计算的原理
(4)对蝶形运算的推导与原理的理解不透彻
(5)编程过程中对变址计算即对按位与的变换形式的不理解
2、解决的方法:
(1)到图书馆借相关的书籍理解相关的原理和过程
(2)到百度收索相关的资料促进理解相应的原理过程
(3)向学长学姐请教或老师的指导
七、总结
<span style="font-size:18px;">#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define N 1000
/*定义复数类型*/
typedef struct{
double real;
double img;
}complex;
complex x[N], *W; /*输入序列,变换核*/
int size_x=0; /*输入序列的大小,在本程序中仅限2的次幂*/
double PI; /*圆周率*/
void fft(); /*快速傅里叶变换*/
void initW(); /*初始化变换核*/
void change(); /*变址*/
void add(complex ,complex ,complex *); /*复数加法*/
void mul(complex ,complex ,complex *); /*复数乘法*/
void sub(complex ,complex ,complex *); /*复数减法*/
void output();/*输出快速傅里叶变换的结果*/
int main()
{
int i; /*输出结果*/
system("cls");
PI=atan(1)*4;
printf(" 输出DIT方法实现的FFT结果\n");
printf("Please input the size of x:\n");//输入序列的大小
scanf("%d",&size_x);
printf("Please input the data in x[N]:\n");//输入序列的实部和虚部
for(i=0;i<size_x;i++)
{
printf("请输入第%d个序列:",i);
scanf("%lf%lf",&x[i].real,&x[i].img);
}
printf("输出倒序后的序列\n");
initW();//调用变换核
fft();//调用快速傅里叶变换
printf("输出FFT后的结果\n");
output();//调用输出傅里叶变换结果函数
return 0;
}
/*快速傅里叶变换*/
void fft()
{
int i=0,j=0,k=0,l=0;
complex up,down,product;
change(); //调用变址函数
for(i=0;i< log(size_x)/log(2) ;i++) /*一级蝶形运算 stage */
{
l=1<<i;
for(j=0;j<size_x;j+= 2*l ) /*一组蝶形运算 group,每个group的蝶形因子乘数不同*/
{
for(k=0;k<l;k++) /*一个蝶形运算 每个group内的蝶形运算*/
{
mul(x[j+k+l],W[size_x*k/2/l],&product);
add(x[j+k],product,&up);
sub(x[j+k],product,&down);
x[j+k]=up;
x[j+k+l]=down;
}
}
}
}
/*初始化变换核,定义一个变换核,相当于旋转因子WAP*/
void initW()
{
int i;
W=(complex *)malloc(sizeof(complex) * size_x); //生成变换核
for(i=0;i<size_x;i++)
{
W[i].real=cos(2*PI/size_x*i); //用欧拉公式计算旋转因子
W[i].img=-1*sin(2*PI/size_x*i);
}
}
/*变址计算,将x(n)码位倒置*/
void change()
{
complex temp;
unsigned short i=0,j=0,k=0;
double t;
for(i=0;i<size_x;i++)
{
k=i;j=0;
t=(log(size_x)/log(2));
while( (t--)>0 ) //利用按位与以及循环实现码位颠倒
{
j=j<<1;
j|=(k & 1);
k=k>>1;
}
if(j>i) //将x(n)的码位互换
{
temp=x[i];
x[i]=x[j];
x[j]=temp;
}
}
output();
}
/*输出傅里叶变换的结果*/
void output()
{
int i;
printf("The result are as follows:\n");
for(i=0;i<size_x;i++)
{
printf("%.4f",x[i].real);
if(x[i].img>=0.0001)printf("+%.4fj\n",x[i].img);
else if(fabs(x[i].img)<0.0001)printf("\n");
else printf("%.4fj\n",x[i].img);
}
}
void add(complex a,complex b,complex *c) //复数加法的定义
{
c->real=a.real+b.real;
c->img=a.img+b.img;
}
void mul(complex a,complex b,complex *c) //复数乘法的定义
{
c->real=a.real*b.real - a.img*b.img;
c->img=a.real*b.img + a.img*b.real;
}
void sub(complex a,complex b,complex *c) //复数减法的定义
{
c->real=a.real-b.real;
c->img=a.img-b.img;
}
</span>







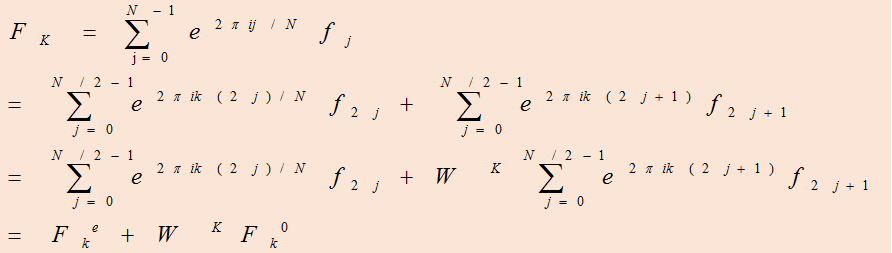

















 7293
7293

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










