机器学习模型代码自我复现：贝叶斯线性回归

最新推荐文章于 2024-05-01 23:06:00 发布

thorn_r

最新推荐文章于 2024-05-01 23:06:00 发布

阅读量624

点赞数 2

文章标签：线性回归算法回归

本文链接：https://blog.csdn.net/thorn_r/article/details/131058511

版权

根据模型的数学原理进行简单的代码自我复现以及使用测试，仅作自我学习用。模型原理此处不作过多赘述，仅罗列自己将要使用到的部分公式。

如文中或代码有错误或是不足之处，还望能不吝指正。

代码有很大一部分参考了利用马尔可夫链蒙特卡洛（MCMC）进行贝叶斯线性回归和非线性回归的python代码（不调包）_贝叶斯非线性回归_Remote Sensing的博客-CSDN博客中的内容，因此本文仅做自我学习的一个笔记。

贝叶斯派视角

之前复现的机器学习中，大多数都是按照频率派的思路进行点估计。以线性回归举例，按照频率派的思想，就是将估计值 $\widehat{y}$ 与真实值 $y$ 的误差平方和作为损失函数，找到能够使得它最小的权重矩阵W，也就是我们常看到的最小二乘法。

而到了贝叶斯派的眼中，原本应该是一个作为“估计值”的W矩阵，本身也是一个符合某一变量的随机变量。我们想要找的是一个分布： $P(W|X,Y)$

由联合概率分布公式，可得 $P(W|X,Y)=\frac{P(W,Y|X)}{P(Y|X)}=\frac{P(Y|W,X)P(W)}{\int P(Y|W,X)P(W)dw}$

其中， $P(Y|W,X)$ 代表似然函数， $P(W)$ 代表先验，可以事先给定。而 $\int P(Y|W,X)P(W)dw$ 是一项归一化常数，可以认为与权重W无关。由此，我们可以得出：

$P(W|X,Y)\propto P(Y|W,X)P(W)$

倘若我们假设 $P(Y|W,X)$ 与 $P(W)$ 均符合正态分布，那么根据正态分布的自共轭性质，后验P(W|X,Y)也符合正态分布。在实际操作中，我们对 $P(Y|W,X)P(W)$ 进行采样，得到许多的W的可能得值，用以近似P(W|X,Y)的分布（主要是求期望方差，在数据量大的情况下，期望会接近最小二乘点估计的结果）。

MCMC采样

MCMC是针对某个概率分布的采样方法。他的基本思路是找到一个平稳分布的马尔科夫链，在这样的马尔科夫链上做随机游走，获得的样本就正好符合我们需要采样的分布。
所以这件事的难点，就是想要找到一个能够使得马尔科夫链收敛的一个状态转移矩阵M，使得 $\pi_im_{ij}=\pi_jm_{ji}$

通常使用Metropolis-Hastings方法来解决转移矩阵难以寻得的问题。
由于直接寻找M相当困难，我们在公式两边同时乘以一个数alpha: $\pi_im_{ij}\alpha_{ij}=\pi_jm_{ji}\alpha_{ij}$
其中， $\alpha_{ij}=min({\frac{\pi_jm_{ji}}{\pi_im_{ij}},1})$

这个α的用处就是将原本不符合细致平稳条件的M作修正。由此，马尔可夫链经过预烧期（一定次数的随机游走）后，最终一定能够收敛到一个平稳的分布，这是马尔科夫链在上随机游走得到的点便正好符合 $\pi M$ 的分布

算法流程为：
1、随机生成初始样本点 $\theta$
2、从已知分布q中随机生成一个候选点 $\theta^{*}$
3、计算接受率 $\alpha=min({\frac{p(\theta^{*})q(\theta|\theta^{*})}{p(\theta)q(\theta^{*}|\theta)},1})$
对于“对称”的已知分布Q, $q(\theta|\theta^{*})=q(\theta^{*}|\theta)$ ，那么公式就可以进一步简化
4、生成0~1的随机数与接受率α比较，大于α时拒绝样本，依然使用样本点θ，否则接受并更新θ为θ*。注意无论是否更新，θ始终会作为样本点加入最后的结果中。
5、重复3、4步获得N个样本点，在经过预烧期后，这些样本点的分布符合我们期望的分布p

class MCMC_gaussian:
    """
    使用metropolis_hastings算法进行MCMC采样，
    获得符合正态分布的n_sampling个点
    由于高斯分布对称性，所以在算法中完全不用涉及转移矩阵M
    参考：https://blog.csdn.net/RSstudent/article/details/122636064?spm=1001.2014.3001.5502
    
    self.mu:正态分布的期望
    self.sigma:正态分布的方差，维度须和期望相对应
    self.burn:预烧期,马尔科夫链游走这个步数后认为其收敛
    self.samplings:要采样的点的数量，实际会返回这个值减去预烧期的步数
    
    """
    def __init__(self,mu=np.array([[0]]),sigma=np.array([[1]]),n_burn=1000,n_samplings=10000):
        if mu.shape[0] != sigma.shape[0]:
            raise ValueError("均值和方差维度不符合")
        self.mu = mu
        self.sigma = sigma
        self.burn  = n_burn
        self.samplings = n_samplings
        self.dim = self.mu.shape[0]
        self.results = np.zeros((self.dim,self.samplings),np.float32)
    
    def gaussian_prob_function(self,x,mu,sigma):
        return np.exp(-(1/2)*np.dot(np.dot((x-mu).T,np.linalg.inv(sigma)),(x-mu)))/(np.power(2*np.pi,self.dim/2)*np.sqrt(np.linalg.det(sigma)))
    
    def MH(self):
        x_old = np.random.uniform(-1,1,size=(self.dim,1))
        
        for i in range(self.samplings):
            #进行一轮随机游走
            x_new = np.random.uniform(-1,1,size=(self.dim,1))+x_old

            #计算接受率
            alpha = np.min([self.gaussian_prob_function(x_new,self.mu,self.sigma)/self.gaussian_prob_function(x_old,self.mu,self.sigma),1])
            if np.random.rand()<alpha:
                #接受样本
                x_old=x_new
            self.results[:,i]=x_old.reshape(self.dim,)
        return self.results[:,self.burn:]

test = MCMC_gaussian()
res = test.MH()

import seaborn as sns

sns.displot(res[0],kind="kde")

import statsmodels.api as sm
import pylab

sm.qqplot(res[0], line='s')
pylab.show()

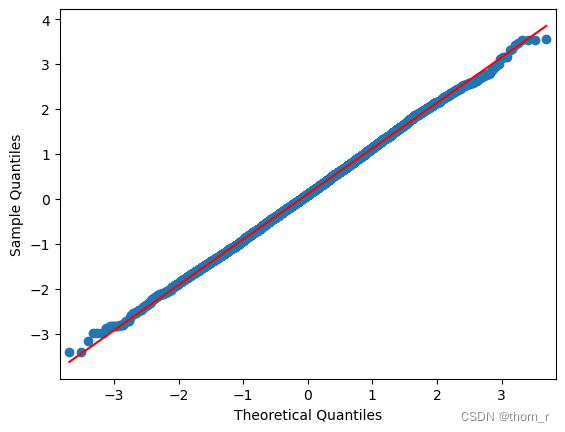
从QQ图上能够看出成功采样到了正态分布，且从分布图上看期望为0。

使用MCMC做贝叶斯线性回归

class Bayesian_Linear:
    """
    参考：https://blog.csdn.net/RSstudent/article/details/122705886
    假设先验与似然函数均符合正态分布，这样只需要统一给出期望与方差2个参数就行了
    self.prior_mu:先验的期望
    self.prior_sigma:先验的方差，维度须和期望相对应
    self.burn:预烧期,马尔科夫链游走这个步数后认为其收敛
    self.samplings:要采样的点的数量，实际会返回这个值减去预烧期的步数
    """
    def __init__(self,prior_mu,prior_sigma,n_burn=1000,n_samplings=10000):
        self.prior_mu = np.array(prior_mu).reshape((len(prior_mu),1))
        self.prior_sigma = np.eye(len(prior_sigma))
        for i,j in enumerate(prior_sigma):
            self.prior_sigma[i][i] = j
        self.dim = len(prior_mu)
        self.burn  = n_burn
        self.samplings = n_samplings
        self.results = np.zeros((self.dim,self.samplings),np.float32)
        
    def gaussian_prob_function(self,x,mu,sigma):
        if x.shape[0] == 1:
            x = x[0][0]
            mu = mu[0][0]
            return (1/np.sqrt(2*np.pi*sigma))*np.exp(-np.power(x-mu,2)/(2*sigma))
        return np.exp(-(1/2)*np.dot(np.dot((x-mu).T,np.linalg.inv(sigma)),(x-mu)))/(np.power(2*np.pi,mu.shape[0]/2)*np.sqrt(np.linalg.det(sigma)))
    
    def likelihood(self,weight,x,y):
        likely_value = 1
        for i in range(x.shape[0]):
            tmp_x = x[i,:]
            tmp_x = tmp_x.reshape([tmp_x.shape[0],1])
            tmp_y = y[i]
            mean = np.dot(weight.T,tmp_x)
            mean = np.array(mean.flatten()[0]).reshape((1,1))
            tmp_y = np.array(tmp_y).reshape((1,1))
            # print(mean,tmp_y)
            # print(mean.shape,tmp_y.shape)
            likely_value *= self.gaussian_prob_function(tmp_y,mean,1)
        return likely_value
    
    def priori(self,weight):
        return self.gaussian_prob_function(weight,self.prior_mu,self.prior_sigma)
    
    def posterior(self,weight,x,y):
        return self.priori(weight)*self.likelihood(weight,x,y)
    
    def fit(self,x,y):
        # weight_old = np.zeros((self.dim,1))#np.random.uniform(-1,1,size=(self.dim,1))
        weight_old = np.random.uniform(-1,1,size=(self.dim,1))
        
        for i in range(self.samplings):
            #进行一轮随机游走
            # weight_new = np.random.uniform(-1,1,size=(self.dim,1))+weight_old
            weight_new = np.random.normal(loc=weight_old,scale = 1,size=(self.dim,1))

            #计算接受率
            alpha = np.min([self.posterior(weight_new,x,y)/self.posterior(weight_old,x,y),1])
            if np.random.rand()<alpha:
                #接受样本
                weight_old=weight_new
            self.results[:,i]=weight_old.reshape(self.dim,)
            if i%1000==0:
                print(i,np.mean(self.results[:,:i+1],axis=1))
        return self.results[:,self.burn:]

倘若想要使用正态分布做其他模型的采样（如非线性回归），只需要将似然函数（likelihood）中的mean变量调整为对应的模型表达即可。

自己构造的数据集：

N = 100
X1 = np.random.rand(N)
X2 = np.random.rand(N)
epsilon = np.random.randn(N)*0.01

y = 3*X1+7+epsilon+5*X2

#缺陷：N过大时会很慢且不再准确；参数过多时不再有用（包括截距项在内3个参数就不准确了）
#似乎有环境依赖？我在老电脑上跑的就很快而且三个参数能拟合出来

test = Bayesian_Linear(prior_mu=[2.5,3,5],prior_sigma=[30,30,30],n_burn=1000,n_samplings=10000)
res = test.fit(np.c_[X1,X2,np.ones((N,1))],y.reshape(N,1))
print(np.mean(res,axis=1))

每1000次迭代的结果：

最终结果：

可以看到3个权重分布的期望已经相当接近真实值了。

在Python中，我们也有自带的包pymc3可以用于贝叶斯建模：

import warnings
warnings.filterwarnings("ignore")
import pymc3 as pm
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

N = 1000
X1 = np.random.normal(loc = 3,scale = 2,size = N)
X2 = np.random.normal(loc = -2,scale = 1.5,size = N)
epsilon = np.random.randn(N)

y = 3*X1+5*X2+3+epsilon

model = pm.Model()
with model:
    alpha1 = pm.Normal('alpha1',mu=0,sd=5)
    alpha2 = pm.Normal('alpha2',mu=0,sd=5)
    C = pm.Normal('constant',mu=0,sd=5)
    sigma = pm.HalfNormal("sigma",sd=1)
    mu = alpha1*X1+alpha2*X2+C
    Y_obs = pm.Normal("obs",observed=y,mu=mu,sigma=sigma)

map_estimate = pm.find_MAP(model=model)
print(map_estimate)

可以看到，pymc3的结果接近模拟数据的真实值。

贝叶斯建模与传统频率派不同，将参数视作符合某一分布的随机变量，并且可以考虑先验分布使得在建模时能够有更高的可信度；然而由于计算复杂度大，必须使用采样法或变分法，可能会使得计算精确度下降，并且增加时间成本。

thorn_r

关注

2
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
机器学习模型代码自我复现：贝叶斯线性回归

贝叶斯建模与传统频率派不同，将参数视作符合某一分布的随机变量，并且可以考虑先验分布使得在建模时能够有更高的可信度；然而由于计算复杂度大，必须使用采样法或变分法，可能会使得计算精确度下降，并且增加时间成本。
复制链接

扫一扫