机器学习之logistic回归的梯度上升算法

机器学习之logistic回归的梯度上升算法

算法背景：

一般来说，回归模型一般不用在分类问题上，因为回归是连续型模型，而且受噪声的因素很大，但是，若需要选择，可以选择使用logisti 回归。

对数回归本质上是线性回归，只是在特征到结果的映射里加入了一层函数映射，选择g(z)=1/(1+exp（-z）)作为sigmoid函数进行映射，可以将连续值映射到0-1之间。

其中g(z)函数的图像如下：可以看到，函数的取值始终在0-1之间。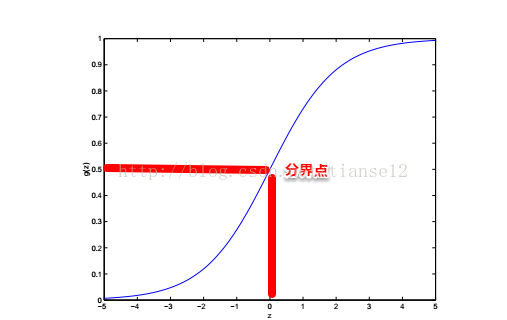

对于分类问题，我们可以建立假设：

          if（z >= 0.5） g(z)=1;  if（z < 0.5） g(z)=0;

算法思想：

对于输出值为y={0,1}的两类分类问题，我们做出一个假设

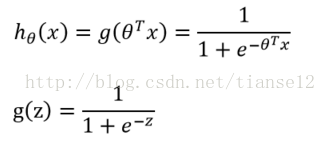
函数g(z)即为上文提到的sigmoid函数，其导数形式为：

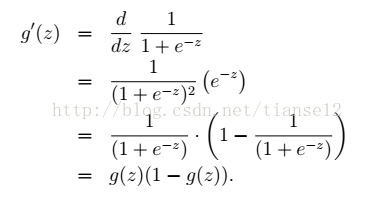
根据这个函数，我们可以得到对于一个样本的概率分布为：