儒略历由来 / 儒略日计算公式 / 历法演化

儒略日的由来

背景，历史、演变、推算，以及在古代与现代的应用场景和具体举例

儒略历

先讲一下儒略历，儒略历是格里历（公历）的前身，由罗马共和国独裁官儒略・恺撒（Julius Caesar）采纳埃及亚历山大的希腊数学家兼天文学家索西琴尼计算的历法，在公元前 45 年 1 月 1 日起执行，取代旧罗马历法的一种历法。一年设 12 个月，大小月交替，四年一闰，平年 365 日，闰年于二月底增加一闰日，年平均长度为 365.25 日。（来自维基百科）

儒略历一直用到大约 1582 年，这时各国开始使用罗马历法。在儒略历里面， 一年是近似 365 1/4 天 = 365.25 天。 这样大约每 128 年就有一天的误差。由于累积误差随着时间越来越大，促使教皇格里高利十三世（Gregory XIII）按照与弥撒议会 （ Council of Trent）一致的精神改革了历法，变为格里历，即沿用至今的公历。在罗马历法里，一年是近似 365 + 97 / 400 天 = 365.2425 天。因此对应于罗马历法，大约要 3300 年，才会积累一天的误差。（本段根据维基百科与其他来源修改）

儒略日

儒略日（Julian day）是指由公元前 4713 年 1 月 1 日，协调世界时中午 12 时开始所经过的天数，多为天文学家采用，用以作为天文学的单一历法，把不同历法的年表统一起来。

儒略日是一种不用年月的长期纪日法，简写为 JD。是由法国学者 Joseph Justus Scliger（1540–1609）在 1583 年所创，这名称据说是为了纪念他的父亲 —— 意大利学者 Julius Caesar Scaliger（1484–1558）。

儒略日的起点订在公元前 4713 年（天文学上记为 -4712 年）1 月 1 日格林威治时间平午（世界时 12:00），即 JD 0 指定为 4713 B.C. 1 月 1 日 12:00 UT 到 4713 B.C. 1 月 2 日 12:00 UT 的 24 小时。

每一天赋予了一个唯一的数字，顺数而下，如：1996 年 1 月 1 日 12:00:00 的儒略日是 2450084。这个日期是考虑了太阳、月亮的运行周期，以及当时收税的间隔而订出来的。Joseph Scliger 定义儒略周期为 7980 年，是因 28、19、15 的最小公倍数为 28×19×15=7980。其中：

28 年为一太阳周期 (solar cycle)，经过一太阳周期，则星期的日序与月的日序会重复。

19 年为一太阴周期，或称默冬章 (Metonic cycle)，因 235 朔望月 = 19 回归年，经过一太阴周期则阴历月年的日序重复。

15 年为一小纪 (indiction cycle)，此为罗马皇帝君士坦丁（Constantine）所颁，每 15 年评定财产价值以供课税，成为古罗马用的一个纪元单位，

故以 7980 年为一儒略周期，而所选的起点公元前 4713 年，则是这三个循环周期同时开始的最近年份。

以儒略日计日是为方便计算年代相隔久远或不同历法的两事件所间隔的日数。

由于儒略日数字位数太多，国际天文学联合会于 1973 年采用简化儒略日（MJD），其定义为 MJD = JD– 2400000.5。MJD 相应的起点是 1858 年 11 月 17 日世界时 0 时。

儒略日的应用

在古代，儒略日主要用于天文学和历法学领域。例如，古代天文学家可以通过儒略日来计算太阳、月亮和行星的位置和运动轨迹，以便预测日食、月食和其他天文现象。而历法学家则可以利用儒略日来比较不同历法之间的精度和误差，以及进行历法的改革和校准。

在现代，儒略日的应用范围更为广泛。例如，GPS 卫星系统就利用儒略日来记录和计算卫星的位置和运动轨迹，以便实现定位和导航功能。此外，儒略日还被广泛应用于航天、地球科学、气象学、物理学等领域。

儒略年

这是天文学中测量时间的测量单位（符号：a），定义的数值为 365.25 天。因为儒略年只是测量时间的单位，并没有针对特定的日期，因此儒略年与儒略历或任何其他的历都没有关联。

天文学家和其他科学家使用它是为了方便测量长的时段，例如，冥王星的轨道周期是 248 儒略年（248a），比用 90,590 日更容易表达。一百个儒略年（36,525 日）称为儒略世纪，一千个儒略年（365,250 日）称为儒略千年。这个单位是用来计算太阳系的历表。
儒略年（符号：a）是天文学中测量时间的测量单位，定义的数值为 365.25 天，每天为国际单位的 86400 秒，总数为 31,557,600 秒。

这个数值是西方社会早期使用儒略历中年的平均长度，并且是这个单位的名称。然而，因为儒略年只是测量时间的单位，并没有针对特定的日期，因此儒略年与儒略历或任何其他的历都没有关联，也与许多其他型式年的定义没有关联。

儒略年既不是测量上的基本单位，也不是被国际单位制（SI）认可的单位。不过，天文学家和其他科学家使用它是为了方便测量长的时段，作为以天表达会笨拙不便的时间单位。因为儒略年是日的累积，使用时也会让人误解，也难怪多数人将它当成是年。例如，冥王星的轨道周期是 248 儒略年（248a），比用 90,590 日更容易表达。

由于这个缘故，国际天文联合会（IAU）才会推荐儒略年是定义距离测量单位光年的基础。一百个儒略年（36,525 日）称为儒略世纪，一千个儒略年（365,250 日）称为儒略千年。这个单位是用来计算太阳系的历表。

历元是天文学上特殊的一个明确的瞬间。为了实用的缘故，每 50 年会选择一个新的历元标准。现在的历元标准是儒略历元 J2000.0。它正确的时刻是 TT 格里历（不是儒略历）2000 年 1 月 1 日 12:00 (很接近格林威治平正午，但不是恰好)。在名称里的 J 表示在之前或之后的其他历元也都是儒略年 365.25 日的间隔。例如，未来的历元 J2100.0 的却时间隔是从 J2000.0 起间隔 36,525 日（儒略世纪）的 2100 年 1 月 1 日（日期仍然相同是因为格里世纪 2000-2100 与儒略世纪的日数相同）。

因为儒略年不会与格里历一年的长度相同，天文学的历元会与格里历的日期在数百年后产生分歧。从地球测量的天体位置和事件，会随着时间变化。因此，当测量或预报天体位置时，都必需配属和指定适当的历元。儒略年，是一致的时间间隔，不要与在漫长的历史岁月里会变动的儒略历混淆。

天文学上的儒略年从未被编予序号，天文学家也跟世界各地一样遵守历法大会的决议：在 1582 年 10 月 15 日格里历被介绍之后开始采用格里历（或因为国家与地区的不同而稍晚），而在之前使用的是儒略历。儒略年不能和天文上使用的儒略日（还有儒略记日或 JDN）混淆。尽管名称很相近，但二者之间的关连却很少。儒略日是从指定的，被称为起始历元的参考日期开始所经历（累计）的整数日数。儒略日是单一的以日计数不参考任何历中的日、月或年，是特殊的只有日和十进制小数下的时间。

附 ：天文学史研究专家 江晓原文章

标题：《儒略历还是格里历 —— 再谈关于历史事件日期的推算与表达》

http://shc2000.sjtu.edu.cn/0708/rulueli.htm（链接已沉寂）

原载于《中国国家天文》2007 年第 4 期

本刊 2007 年第 2 期上卞毓麟先生的文章《从牛顿生日谈历法》，对儒略历和格里历的异同讲得非常清楚。但是许多对历史很感兴趣的人士，对于在表达历史事件的日期时，如何在这两部历法中取舍，以及天文学界和历史学界在与此有关的问题上的通行约定和规则，常有不甚了了之处，甚至有着很流行的误解。

许多人看到对公元前某个历史事件发生日期的陈述，比如武王伐纣的牧野之战发生于公元前 1044 年 1 月 9 日，或孔子诞生于公元前 552 年 10 月 9 日，就会发出疑问：这些日期是儒略历的还是格里历的？当他们得知这些都是儒略历的日期时，往往会接着产生更大的疑问：既然格里历比儒略历精确，为什么还要用儒略历？有的人甚至一看到天文学家使用儒略历表达公元前日期，就以为发现了天文学家的大错误，立刻信口雌黄起来，认为那些天文学家都是些欺世盗名之徒 —— 连儒略历和格里历该用哪个都搞不清楚。

其实这是因为他们不知道，“推算历史事件的日期” 和 “表达历史事件的日期”，是两件不同的事情；此外他们对某些学术界的某些共同约定也缺乏了解。

事实上，天文学家在推算一个历史事件发生的日期时，既不使用儒略历也不使用格里历，而是使用 “儒略日”—— 没有年、月单位，只有日的计时体系（要是钻牛角尖，可以说这仍是对时间坐标的一种表达）。例如，武王伐纣的牧野之战发生于 “儒略日” 1340111 日，孔子诞生于 “儒略日” 1520087 日，笔者写这篇文章的这天（2007 年 5 月 1 日）是 “儒略日” 2454222 日，等等。而 “儒略日” 与公历之间的对应关系是明确的：“儒略日” 起算点为公元前 4713 年 1 月 1 日（儒略历）。

当天文学家推算出一个历史事件的日期之后，当然需要将它 “表达” 出来；而为了便于公众理解和接受，如果表达成 “孔子诞生于儒略日 1520087 日” 显然是不合适的，所以要用我们熟悉的公历来表达。

公历在公元 1582 年处形成了一个分界 —— 这一年罗马教皇格里高利十三世颁布了格里历，并在一些天主教国家开始使用。这个分界带来了一些容易让人误解的问题。而针对这些问题我们需要一些约定。

一，对于公元 1582 年以后的日期，都用格里历表达，这毫无问题。

二，对于从公元前 46 年（儒略历开始使用）到公元 1582 年，这一千六百多年中的日期，当然使用儒略历来表达，因为那时格里历还不存在。

三，对于公元前 46 年之前的日期，我们应该用什么历法来表达呢？不少人因为误以为对于历史事件的日期就是用 “历法” 推算的，而格里历又比儒略历精确，就想当然地认为应该用格里历来表达。但是仔细一想，事情并非那么简单。

首先，在公元前 46 年之前，既没有儒略历也没有格里历。当然，在那时的世界各文明中，已经存在着多种多样的历法，比如埃及的历法、罗马的历法、中国的历法，等等。但是我们今天要将一个历史事件的日期给出一个全世界都能够理解的表达，当然不能仅仅使用当地的历法。所以公元前 46 年之前的日期用哪种历法来表达，必须有所约定。

国际历史学界和天文学界的约定，是将公元前 46 年之前的日期统一用儒略历来表达。这一约定也许是不成文的，但确实是合理的。因为公元前 46 年之后开始使用儒略历，那么将这一历法向公元前 46 年之前的年代延伸，是很自然的；如果使用格里历来向公元前 46 年之前的年代延伸，就要跳过一千六百多年，这显然不合常理。

事实上，用哪种历日来表达一个历史事件的日期，与儒略历和格里历哪个更精确没有任何关系。

公历在公元 1582 年处的分界，还带来另外一个问题：由于全世界各国并非都在公元 1582 年就开始使用格里历，许多国家几十年甚至几百年后才接受格里历（比如中国直到 1912 年才开始使用），所以在 1582 年至 20 世纪初（那时世界各国才普遍使用格里历）这三百多年间，许多历史事件就会有两个日期 —— 比如牛顿的生日就有 1642 年 12 月 25 日（儒略历）和 1643 年 1 月 4 日（格里历）两种表达，“十月革命” 则有 1917 年 10 月 25 日（儒略历）和 1917 年 11 月 7 日（格里历）两个日期。

这两个日期应该采用哪个，也不是轻易就能有一言九鼎的结论的。通常人们都使用儒略历的那个，那是因为英国直到 1752 年、俄国直到 1919 年才使用格里历，在牛顿出生、“十月革命” 爆发时，事件发生的国家都还在使用儒略历。

---

历法的进步 —— 从牛顿的生日谈起

中国科学院理化技术研究所 戴闻 发布时间：2010-07-21

Development of calendar rules——Starting with Newton’s birthday

2003 年夏，火星与地球间的距离达到极小，是发射火星探测器的好时机。从这年 6 月起，日本、欧洲和美国相继发射火星探测器。长距离的飞行耗时近 7 个月，这些航天器预计从 12 月起陆续接近火星。

欧洲航天局的火星快车 (Mars Express) 一路顺风，在接近火星的期间（12 月 19 日），将搭载的小型登陆探测器 —— 猎兔犬 2 号（Beagle 2, 注: Beagle 1 是达尔文 19 世纪 30 年代在探险旅途中乘坐的一艘英国皇家海军舰艇）“抛向” 火星。猎兔犬 2 号预定于 12 月 25 日格林尼治时间 2:45 登陆火星，这一天正值圣诞节，又是伊萨克・牛顿的生日（按照旧历）。不幸，猎兔犬 2 号的降落伞没有及时打开，登陆探测器可能已经坠毁于火星表面。美国发射的 2 辆火星车 —— 勇气号（Spirit）和机遇号（Opportunity）分别于 2004 年 1 月 4 日 4：35 和 1 月 26 日成功登陆火星。勇气号几经磨难，终于起死回生。无巧不成书，勇气号登陆火星的日子，也是牛顿的生日。按照现在国际通行的历法 —— 格里高利历，牛顿的出生日是 1643 年 1 月 4 日。这就是说，勇气号的成功登陆正值牛顿 361 年诞辰；361＝192＝围棋盘上的格点数，又是一个吉祥的数字。

有迷信者，把勇气号的成功说成是 “黄历” 和 “风水” 的作用。事实上，二者风马牛不相及。科学家选择登陆的日期，或许隐含有 “纪念牛顿” 的目的，但执行计划时必须服从技术要求。无论是发射之前还是之后，如果遇到技术困难不得不改变飞行时刻表，科学家一定会毫不犹豫地选择能够保证成功登陆的方案。这就是所谓，科学的可修正性。相反，黄历的制定说不出任何道理，它只是根据一套死规矩，预言：× 月 × 日不宜出行，× 月 × 日不宜动土等等。

1 西方历法

猎兔犬 2 号和勇气号着陆火星的日期前后相差 10 天，但又都正值牛顿的诞辰，让我们来看其中的缘由。

我们现行的历法称为格里高利历（Gregorian Calendar），它是于 1582 年由教皇格里高利十三世颁布并首先在天主教国家实施的。按照格里高利历，平年每年有 365 天，闫年是 366 天；不能被 4 除尽的年份为平年，能够被 4 除尽的为闰年（但是，其中能够被 100 除尽的不闰，而能够被 400 除尽的要闰）。这样，1900 年不是闰年，但 2000 年是闰年。考虑 2000 年的时间跨度，按照 “4 年除尽” 有 500 个闰年，去掉 20 个 “100 除尽” 不闰，再加上 5 个 “400 除尽” 闰，结果是 485 个闰年。于是，按照格里高利历，在一个 2000 年的时间跨度上，逝去的天数是 730485。这就是说，格里高利历的回归年长度（从夏至日影最短的时刻到下一个日影最短的时刻）被人为地规定为 730485／2000＝365. 2425 天。

现代天文观测给出的回归年实际长度是 365. 2422 天（严格说，应称为平均太阳日）。在 1000 年的期间，回归年长度的实际值与格里高利历设定值之间的累计误差只有 0.3 天。这表明，格里高利历的规定是相当合理的。现行的历法中没有考虑对上述误差的补正。或许在将来（公元 3300 年以后），可以通过国际协商，删去一个闰日，予以补救。

在格里高利历实施之前，欧洲普遍实施的是儒略历（Julian Calendar）， 它是公元前 46 年由儒略・凯撒（罗马大帝）颁布的历法。这一历法规定：平年 365 天，闰年 366 天，每 4 年有一个闰年。这样一来，每 100 年必定有 25 个闰年。结果，按照儒略历，回归年长度的设定值是 365 25 天。这个值相对于实际值的偏离，要比格里高利值的偏离大得多。因此，随着时间的推移，儒略历所产生的误差增加很快。如果共同约定了一个时间原点（例如，公元元年 1 月 1 日 0 时 0 分），在若干年之后，问起：我们度过了多少天？大家不会有分歧。因为这个天数严格等于日出（日落）的次数，它是客观的。另一方面，如果问：某一天是几月几日？则会产生矛盾。因为这涉及到历法，也即涉及到记年的标尺单位。格里高利的年长度单位小于儒略历，结果用格里高利历读出的日期就将大于儒略历的读出值。

1582 年之所以要对旧历 —— 儒略历进行改革，是因为按照儒略历记录的日期已经与季节的概念不同步了。例如，原来的概念，6 月 22 日是夏至；可到了 1582 年，夏至（太阳影子最短的时刻）却出现在儒略历的 6 月 12 日。按照儒略历，回归年长度是 365.25 天，按照格里高利历则是 365.2425 天，经过了 1582 年，二者之间的累计误差已接近 12 天。只是由于某些细节上的原因，新历（格里高利历）规定：将日期从儒略历的 “读出值” 向后推 10 天。

在保守的英国，直到 1752 年才进行历法的改革，以至于牛顿出生时英国实施的仍是儒略历。因此，甚至在《大英百科全书》中，牛顿的生日也是按旧历给出的 ——1642 年 12 月 25 日。然而，按照今天全球普遍采用的格里高利历，说牛顿出生于 1643 年 1 月 4 日，也是完全正确的。

在德国，各地区采用格里高利历的起始年代不一，美因兹地区从 1667 年开始采用，而汉诺威地区是从 1676 年开始。美因兹侯爵和汉诺威公爵先后同意实施历法改革，都是由于数学家莱布尼茨（Leibniz G W ）的竭力劝说和推动。莱布尼兹与牛顿并称为微积分的创始人。莱布尼茨是第一任柏林科学院院长，并且是英国皇家学会会员和巴黎科学院院士。

在俄国，格里高利历的采用是在 1917 年之后，十月革命发生在旧历 10 月 25 日，但今天人们在 11 月 7 日纪念这个节日。

由于地球自转速率存在起伏，在 20 世纪 50 年代，国际上的标准秒是通过回归年的平均长度来定义的。1 秒等于 1 年时间的 31 556 925. 9747 分之一，或者说，1 天（平均太阳日）＝86400 秒，1 年＝365.2422 天。为了复现这一标准，需要做长期烦琐的天文观察，并且精度只能达到 1／109。1964 年国际计量委员会通过议案，规定：以 133Cs 原子基态的超精细能级差来定义秒，并通过原子钟来实现。今天，计量用的原子钟已经达到了 1／1014 的精度，换句话说，每 300 万年才会产生 1 秒的误差。

历法的制定原本在于 “过一天算一天”，不要把日子算错了。依照今天的原子钟，人们早已达到了 “过一秒算一秒” 的水平。并且，反过来，用原子钟还可以测量出地球自转速率的不均匀。近年来的测量数据表明，实际（平均太阳日）日长＝86400 秒＋△，△约在 1ms 到 3ms 之间。为了对累计起来的误差进行修正，设在巴黎的国际时间局，每隔一、两年就要通令全世界的 “标准钟”：添加一个 “闰秒”。

2 现行的农历

中国人历来使用农历，它又被称为夏历。这是一种既基于月球绕地球运行（阴历）又基于地球绕太阳运行（阳历）的历法。在农历中，无论是记天还是记年都采用 “天干－地支” 的轮回，天干包括：甲乙丙丁戊己庚辛壬癸；地支包括：子丑寅卯辰巳午未申酉戌亥。天干每 10 年一循环，地支每 12 年一循环，两者合在一起是 60 年一循环。1644 年明末农民起义失败，郭沫若于 1944 年写了一篇文章《甲申三百年祭》，为了讨论起义失败的教训。按照农历，1644 年、1944 年和 2004 年都是 “甲申年”。“申猴 — 酉鸡 — 戌狗 — 亥猪” 的次序大家都很熟悉，但天干与地支的匹配往往容易出错。从 1894 年 “甲午” 开始（设为序号 1），问你 “序号为 51” 的年份如何标记，如果您的答案是 “甲申”，则说明您已经掌握了匹配法则。

按照我国天文学家席泽宗的研究结果，我们的祖先，从东汉以来，就严格按照 “天干－地支” 记年；从公元前 722 年，就严格按照 “天干－地支” 记天。因此我们很容易将文史资料中的日期转换成公元日期。例如，关于公元 1054 年（宋代至和元年）农历五月 “己丑” 超新星的爆发，按照席泽宗的推算，爆发始于该年的 7 月 4 日（格里高利历）。正确的日期转换对于当代的天文学研究具有重要意义。同时，关于超新星爆发日期的认定，也为各国古代历法之间的沟通架起了桥梁。

关于一个月的长度，格里高利历的规定有任意性，每个月 31 天，30 天，28 天不等。而农历的一个月定义为月相变化的平均周期，它等于 29.530 556 天。如果以恒星为参照系，月球绕地球一周需 27.321 578 天，它之所以小于月相朔望变化的周期，是由于地球带着月球绕太阳公转。参照月相变化的历法，不仅为我国汉族使用，穆斯林和藏族的历法也大致如此。例如，2004 年（甲申－猴年）农历二月初二即为藏历的新年。藏历不以完全看不到月亮的 “初一” 为一个月的开始，而是以极细弯月的出现为一个月的开始。显然，藏历每年开始的季节（岁首）也与农历不同。

与太阳历相比，农历有它的优越性。在通讯与媒体不发达的古代，农民可以凭借月相来判断日期，以至于不误农时。另一方面，农历与公历一样，也是以回归年周期作为一年。农历的 12 个月大约是 355 天，为使每年的夏至大致落在五月份，必须在有的年份增设闰月。

目前，我们采用的是十九年七闰规则，即十九年中有七年包含 13 个月，有十二年包含 12 个月。已知朔望月长度＝29.530 556 天，于是，十九年的总天数＝6939.704 天，平均每年 365.2476 天。这个值略大于实际回归年的长度（365.2422 天），但小于儒略历的 365.25 天。

在十九年中，七个闰月究竟加在哪一年、哪一月，农历有它严格的规定。其前提是，月份要与季节大致同步，或者说，月份要与 24 节气大致同步。具体说，闰月必须没有 “中气”。我们都知道节气排列的顺序：立春 — 雨水 — 惊蛰 — 春分 — 清明 — 谷雨等等。所谓 “中气” 是指其中间隔出现的 “雨水”“春分”“谷雨” 等。2004 年（甲申－猴年）正好赶上闰二月，查一下普通日历就能知道：在 “闰二月” 内，只有清明（闰二月十五）一个节气；而此前的 “中气” 春分在二月卅，此后的 “中气” 谷雨在三月初二。

节气的划分早先是将一个回归年的天数分成 24 等分，结果每 15.218 天设置一个 “节气点”。后来人们发现，在一个回归年中太阳的视运动是不均匀的，将相邻 “节气点” 之间的长度固定为 15.218 天不利于节气与季节间的协调，不利于日食的推算。唐代僧人一行（公元 683－727 年），在大量观测的基础上，首次将太阳视运动不均匀问题用于他所主持制定的历法（大衍历）中。一行将太阳在一个回归年内所走过的角度（现在的 360°）分成 24 等分，并在每一分点设置一个节气。这一规定使得相邻 “节气点” 之间的时间长度各不相同，但更利于历法精度的提高。我们现在 “节气点” 的设定，是以太阳为参照系，地球绕太阳每走过 15° 就碰上一个节气。尽管一行的方案是认为太阳绕地球转，但在节气设定的精度上与现代办法是一样的。按照现代农历，说 “2004 年 4 月 4 日是清明”，是不准确的；事实上，“节气点” 清明有它特定的时刻，正确的说法应该是 “2004 年 4 月 4 日 × 时 × 分 × 秒是清明”。

3 农历 —— 秦汉及其以前

早在春秋战国时期，我们的祖先便认识到：回归年等于 365.25 天，月相变化的周期＝ 29 499 940 29 \frac{499}{940} 29940499​

天，为了使回归年与朔望月长度相互协调，在春秋后期便采用了十九年七闰的规则。这一规则与 365.25 天以及 29 499 940 29 \frac{499}{940} 29940499​天，三者互为因果；很容易验证，从任意二者出发肯定能导出第三者。365.25 天，与古罗马于公元前 46 年实施的儒略历的回归年长度值是一样的，但后者比我国晚了约 500 年。

在秦王朝建立以前，秦国地区使用的颛顼（Zhuan Xu ）历便是一种典型的十九年七闰古历法。颛顼，按照新华字典的解释，是传说中的上古帝王名，可见这一古历法历史的久远。

有人说，我们今天的农历也采用十九年七闰法，是否意味着 2500 年来农历没有进步呢？答案显然是否定的。首先，对于朔望月的长度，今天有了更高精度的数据。结果，同样采用十九年七闰法，我们得到的回归年长度将不是 365.25 天，而是 365.2476 天。如前所述，这个值比原先更为接近 365.2422 天的实际值。其次，在古历法中闰月一般都设置在年终，因此很难实现历法与季节的谐调一致。后来规定 “闰月不包含‘中气’”，合理地解决了这个问题。

秦始皇实现大统一后，通令全国一律采用 颛顼历。此后，“在年终设置闰月” 的缺陷逐步被认识。汉武帝决心组织力量 “议造汉历”。《史记》作者司马迁也是当时的受命重臣之一。汉历的制定，遵从 “制历必先测天” 的原则，而历法的优劣需由天文观测来判定。“闰月不包含‘中气’” 的原则就是在西汉末年提出的，并一直沿用至今。在汉代对于行星运行周期、朔望月、恒星月、近点月和交点月均已有了定量估计；对于天球分度、黄赤交角、黄白交角以及月球轨道视运动的快慢，均已有了专门的测定方法；对于行星逆行、彗星以及超新星的出现，也开始有了规范的记录。

汉代的张衡（公元 78－138 年）是世界公认的古代科学家。利用自制的浑天仪，张衡测定：黄道面与天赤道面的夹角是 24°，与我们今天的精确值（23°27’）一致（注：近代天文学告诉我们，这个倾角是随时间缓慢变化的，所涉及的二类变化的周期分别是 26000 年和 41000 年，见下文）。在张衡的浑天仪中，以漏水为运转动力，利用漏壶滴水的等时性以及齿轮传动，复现每日天象的变化。

4 农历 —— 南北朝 —— 祖冲之

祖冲之（公元 429－500 年）是南北朝 —— 刘宋的数学－天文学家。祖冲之以圆周率的计算闻名于世。祖率＝3.14159265，其精度领先于世界范围内的数学同行学者约 1000 年。他在天文学领域的实践和成就，更是科学精神、科学方法和科学态度的体现。

祖冲之出身于天文 — 历法世家，这使得他的研究起点一开始就较高。然而，他 “不虚推古人”，而是对前人的断言持怀疑态度。他 “搜练古今，博采沈奥”，并长期坚持天文观察 ——“亲量圭尺，躬察仪漏，目尽毫厘，心穷筹策”。

在刘宋 —— 大明六年（公元 462 年），祖冲之完成了大明历的编制，并上书宋孝武帝刘骏，要求进行历法改革。他指出了 19 年 7 闰（注：为清楚起见，以下均用阿拉伯数字表述）在精度上的不足，并提出 “391 年设 144 个闰月” 的改革方案。

如前所述，19 年 7 闰的法则在精度上与儒略历是一样的。那么，祖冲之的方案是否比儒略历更精呢？为了回答这个问题，笔者做了一些运算，记述如下：

已知，朔望月长度＝29.530 556 天，则平年（12 个月）＝354. 366 672 天，闰年（13 个月）＝383.897 228 天。若 391 年中设 144 个闰年和 247 个平年，则 391 年的总天数是 142 809.7688 天，平均每年是 365. 242 375 天。

上述结果表明，按照大明历，回归年的长度值不仅优于儒略历，而且比格里高利历（1 年＝365. 2425 天）更接近实际值（1 年＝365. 2422 天）。在笔者用 10 位计算器进行上述计算时，计算器差一点不能达到所要求的精度。祖冲之的计算是用算筹完成的。不象我们今天的笔算，算筹运算不可能保留中间步骤。从这个意义上讲，祖冲之为了得到上述结果需要何等高超的智慧、技巧和毅力啊！

为了推行大明历、祖冲之在朝廷上与皇帝宠臣戴法兴展开了针锋相对的论战。戴法兴认为，19 年 7 闰的规定是 “古人制章”“不可革”；他攻击祖冲之的大明历，是 “削闰坏章”“诬天背经”。畏于权势，当时在场的朝臣几乎一边倒，都站在戴法兴一边。祖冲之不得不独军奋战，他说，日月星辰的运行，“非出神怪，有形可检，有数可推”，不应该 “信古而疑今”。由于重重阻挠以及改朝换代等历史原因，祖冲之没有在他的有生之年看到大明历的实施。在他儿子祖（日恒）的不懈努力下，大明历于梁 —— 天监九年（公元 510 年）才颁行实施。

历法精度的提高不仅依赖于对太阳和月亮的观测，还需借助于星空 —— 恒星参考系。在北半球冬至的午夜，人们在正南方向看到的是双子座内靠近金牛座的某颗星。然而，在 2 千年前冬至的午夜，人们在正南方向看到的却与今天不同，它或许是双子座内偏向巨蟹座的另一颗星。这一现象的产生，是由于地球自转轴的指向不是固定不变的，而是在缓慢变化。

地球由于自转的离心作用而呈椭球状：沿赤道的纬圈大于过两极的经圈。月球的引力，作用在椭球状的地球上，会产生一个将自转轴 “搬正” 的力矩。这力矩使自转轴进动。进动的方向自东向西，进动过程使地轴在太空中缓慢地扫出一个圆锥面，锥底直径的张角约为 47°，进动周期约为 26000 年。此外，地球自转轴相对于公转轨道平面还有一个 ±2° 的俯仰变化，其变化周期是 4.1 万年。

以恒星为参考系，地球绕太阳走过完整的一周，称为一恒星年。然而，由于上述自转轴的进动，在地球轨道运动尚未走完 2π 的弧长，下一个冬至便来临了。从冬至到下一个冬至称为回归年，显然，回归年长度小于恒星年。现在知道，冬至点每 71.71 年向西移动 1° 角，并将此现象称为 “岁差”。与 2000 年前我们的祖先相比，一年中特定日期特定时刻的星图已经沿赤经向西漂移了近 28°。

早在西汉末年，我国天文学家就已经发现了 “岁差” 现象，对于冬至点每年西移角度的估算，精度逐步有所提高。而到了南北朝的宋冲之，进一步把对岁差的定量估算，应用于大明历的编制中。从某种意义上讲，祖冲之是明确区分 “回归年” 和 “恒星年” 两个概念的先驱。

5 农历 —— 隋唐宋元

无论是月球绕地球的轨道运动还是地球绕太阳的公转，都不是匀速圆周运动。按照近代科学的开普勒第二定律，在近地点附近相对运动的角速度较大，反之角速度较小。为要准确预报日食、月食出现的时刻，必须考虑月球和太阳相对于地球视运动的不均匀性。这类不均匀性已经分别在隋代（考虑月球）和唐代（考虑太阳）的历法中得到了体现。隋唐时期，社会较为稳定，经济繁荣，文化高度发达，这为后来宋、元两代科学技术的高速发展准备了条件。

北宋时期，在 1010－1106 近百年间，进行过 5 次大规模的天文观测。用于观测的巨型铜制浑天仪，每台重量高达 10 吨。其中第四次观测结果被绘成星图，后来（1247 年）又转刻成了著名的 “苏州石刻天文图”。该图包含了 1430 颗恒星以及它们的方位，远远超出了西欧文艺复兴前（14 世纪）记录的恒星数目。大规模观测还发现了恒星位置自古至今的缓慢变化，而恒星的定位精度优于 1° 角。此外，作为这些观测的副产品，关于 1054 年超新星爆发详细栩实的记录，则成为当代天文学研究中子星的宝贵资料。

元代的郭守敬（1231－1316 年）是天文仪器制造和观测领域杰出的科学家，他承先启后组织力量，领导完成了规模空前的测地工作。在 1280－1282 年期间，他主持了 “授时历” 的编制，并加以完善。郭守敬将他发明的 “三次内插法” 用于整理观测数据，使授时历成为当时世界上最先进的历法。

为测定冬至点，郭守敬专门制造了 4 丈高的 “圭表”，并将小孔成像原理用于其中。因此，影长的测量误差被减小到 ±2mm，从而大大提高了回归年长度和黄赤交角的测量精度。按照授时历，地球的近日点与冬至点相合，此间太阳的视运动最快。授时历还明确指出，回归年长度不是永恒不变的，而是古大今小。

宋元时期，中外科技交流发展很快。古希腊天文学家托勒密所著《天文集》，在公元 2－15 世纪是西方天文学的权威著作。这本书的阿拉伯文版就是于 1271 年首次传入我国的。

6 明清时期科技的衰落

明太祖朱元璋从一开始便实行高度强化的极权统治。明代的科举制取消了 “算学科”，规定：必须以八股文体应试。考题仅限于 “四书五经”，并以是否符合 “程朱理学” 来评卷。

尽管为了显示国威完成了 “郑和七次下西洋”，尽管明中叶以后资本主义开始萌芽，但 “自给自足的封闭经济” 仍在那个时期占主导地位。明代统治者进一步严禁民间的历法研究，违者杀头。明朝十几代没有进行过历法改革，一直使用所谓 “大统历”，它实际上就是元代的授时历。只是到了崇祯二年（1629 年），徐光启（1562－1633 年）运用所学到的西方天文知识，在预报天象时 “击败” 了当时的 “钦天监”，他才被任命主持明代唯一的一次历法改革。《崇祯历书》计 137 卷，完成于 1633 年，这部书属于丹麦天文学家第谷体系，对哥白尼、伽里略和开普勒的天文观测也有一些介绍。该书打破了我国历法编制的传统格局，融入了西方传教士带来的数理天文学新方法。

17 世纪初叶，隶属于罗马天主教的耶稣会士来到中国。 这些人以及 200 年之后到来的基督教的牧师们，是近代科学走出欧洲的主要传播者。 耶稣会士以他们的天文以及测地知识，满足了明、清皇室制定精确历法和绘制帝国版图的需求。 而基督教的牧师们带来的工业和军事方面的先进技术，则正好适应了鸦片战争失败前后中国改革派的需求。 遗憾的是，在 1600-1900 三百年间许多最重要的理论和原理并未真正传入。 知识传入被过滤和阻断，部分原因来自传教士本身的宗教承诺和宗教纪律：天主教的耶稣会士拖延牛顿学说的翻译长达一个世纪，基督教的牧师们则用基督教的创世纪解释达尔文学说。 另一方面，这批传教士长期缺乏与欧洲的及时通讯，致使传播跟不上科学的最新进展。 近代科学的传入也曾遇到中国宫廷成员的阻力。 中国的帝制，使得任何知识要想在中国的土壤上扎根，必须首先博得宫廷对其效用的兴趣。 结果，抽象的知识 (如：微积分) 较少受到注意。 中国官方将物理学等称之为” 西学”, 其中包含着某种” 贬意”。 此外，皇室还鼓励中国精英去搜索古代经典，以证明: ” 西学” 只不过是早年中国成就的衍生品。

清朝统治者入关后，基本上沿袭明代的各种制度。统治者对反清力量的镇压以及 “文字狱”，迫使大部分知识分子走上了 “训诂考据” 的道路。清初，曾参与明末历法改革的德国耶稣会士汤若望，将整理修订后的《崇祯历书》—《时宪历》献给顺治皇帝。因此，汤若望被委任为钦天监监正。顺治去世，正值康熙年幼，清廷中以鳌拜为首的保守势力，以 “阴谋不轨” 罪拘捕了汤若望，并判处死刑（后又赦免）。康熙掌权后，为汤若望平了反，《时宪历》也得以颁行，但西方科技的传入在康熙之后的不久（1773 年）就停滞不前了。

---

儒略日计算公式

全都是泡饃 于 2019-07-24 07:35:55 发布

简化版儒略日计算公式

$J D=1721013.5+367 \times Y-\operatorname {int}\{7 / 4 [Y+\operatorname {int}((M+9) / 12)]\}+d+h / 24+ 
\operatorname {int}((275 \times M) / 9)$​​

• 1
• 2

J D = 1721013.5 + 367 × Y − int ⁡ { 7 4 [ Y + int ⁡ ( ( M + 9 ) 12 ) ] } + D + H 24 + int ⁡ ( 275 × M 9 ) JD = 1721013.5 + 367 \times Y - \operatorname{int}\left\{\frac{7}{4}\left[Y + \operatorname{int}\left(\frac{(M+9)}{12}\right)\right]\right\} + D + \frac{H}{24} + \operatorname{int}\left(\frac{275 \times M}{9}\right) JD=1721013.5+367×Y−int{47​[Y+int(12(M+9)​)]}+D+24H​+int(9275×M​)​

精确版儒略日计算公式

$J D=\operatorname {int}(365.25 \times y)+\operatorname {int}[30.6001 \times (m+1)]+D+h / 24+1720981.5$​

• 1

J D = int ⁡ ( 365.25 × Y ) + int ⁡ [ 30.6001 × ( M + 1 ) ] + D + H 24 + 1720981.5 JD = \operatorname{int}(365.25 \times Y) + \operatorname{int}[30.6001 \times (M+1)] + D + \frac{H}{24} + 1720981.5 JD=int(365.25×Y)+int[30.6001×(M+1)]+D+24H​+1720981.5​

---

儒略日与公历转换

方中 已于 2024-05-21 23:16:31 修改

完整代码下载（C++/Python）

https://download.csdn.net/download/weixin_42763614/14917365

提供两种语言的实现。代码中增加对日期格式的输入输出处理。

公历转儒略日

《Astronomical Algorithms》中给出了简便的计算公式。[注2]

书中并未给出公式的含义，这里做一个分析。

儒略历转儒略日

若求 Y 年 M 月 D 日对应的儒略日，即分别对 (Y - 历元年) 年 (M-1) 月 D 日进行积日。

年：
由于公元纪年法没有 0 年，为方便计算，天文学中以 0 表示公元前 1 年，则公元前 4713 年表示为 - 4712。对儒略历而言，以 365.25 天为岁长，每年闰余 0.25 天，4 年闰余积 1 天则需置闰。故儒略历每 4 年一闰。利用取整运算，可以在一个置闰周期中，对于 365.25*(Y-x)，每 4 年前 3 年向下取整，第四年进位。注意 Y 可以是任意一年，x 用于将年份调节为任一置闰周期的起点。计算 Y 年的积日，即将从 - 4712 年到 Y 年的积年乘以一回归年的长度。

floor((Y+4712)*365.25) [注3]

月：

1. 公历设置大小月的基本思路是每月大小相间隔。相邻两月必为 61 天，如此一年共 366 天。平均一月为 30.5 天。故利用取整运算，对于每两个月的周期规律可以使用 int(30.5)，从小月开始，为小月时取其整数，为大月时则会进位 。 这种情况下，M 月（积月为 M-1）的积日即为 int(30.5*(M-1)) 。而公历以单数月为 31 天，双数月为 30 天。即岁首（M=1）时为大月，可令上式 M=M+1，将该式调节到从大月起算，再减去多加的一月 30，则积日为 int(30.5*M)-30

2. 公历一年实际只有 365 日，需在某月中减去一天，而公历设在二月。这时，3~12 月份仍然是有规律的（大小月相隔），1 月有 31 天，2 月有 29 天。如此，可假设以 3 月份作为岁首，2 月为年尾。则在 2 月减去的一天可理解为上年岁末（即今年岁首前）少一天。并以 13、14 月表示上一年的 1、2 月（即一年只有 3~14 月）。则每年仍然是单数月 31 天，双数月为 30 天，且岁首（M=3）仍为大月，则仅需令上式再减 1（2 月少一天）。计算 M 月的积日，则有：int(30.5*M)-31（M>2）

该式只适用于 M>2 的情况，所以当为 1 月或 2 月时，可设为 13、14 月，即 M=M+12，如此则多算一年，即令 Y=Y-1。

一年的状况（单数月31天，双数月30天）
 
3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 1月 2月
 
31天 30天 31天 30天 31天 30天 31天 30天 31天 30天 31天 30天-1

1. 对于公历，又将8月增加一天成为大月，以后9~12月则依次改变大小月顺序，而二月再减去一日成为28天。

一年的状况（每5个月循环）
 
3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 1月 2月
 
31天 30天 31天 30天 31天 31天 30天 31天 30天 31天 31天 30天-2

如此，7、8 成为连大月，12、13 也是连大月。其中 8 月与岁首相差 5 月，13 月与 8 月也相差 5 月。此时的每月的大小顺序仍然存在某种规律，即每连续 5 月，大小月按大小大小大循环排序。亦即连续 5 月的积月为 153 天（3 大 2 小），平均每月为 30.6 天。则 M 月的积日为 int (30.6*M)-31，由于该式是以 3 月为岁首，需调整月份，即令 M=M+1，再减去多算的一月 30，并需减去 2 月再减少的 1 天则有：

int(30.6*(M+1))-62 （M>2）

日：

由于儒略日的历元是以正午12时开始（记为0.0），而公历一日之始以半夜12时开始（记为1.0），两种相差0.5天，则对日的积日为实际日数-1.5

D - 1.5

将儒略历转换为儒略日，仅需将年月日的积日相加，有：

floor(365.25*(Y+4712))+int(30.6*(M+1))+D-63.5 （M>2）
 
当 M <=2 时：令Y = Y - 1，M = M + 12，可适用该公式

格里高利历转儒略日

闰：

儒略历每 400 年百闰。而在 1582 年发现春分点与实际相差 10 日。故以是年 10 月 4 日的次日实行新历（格里高利历），历元为 1582 年 10 月 15 日，有 10 日之差。新历重新测定了回归年长度，岁长改为 365.2425，即每 400 年少 3 日，合 400 年 97 闰。故计算格里高利历的儒略日，还需在上式中减去不置闰（能被 100 整除，但不含能被 400 整除的年份）的日数，即为 - floor((Y-1582)/100)+floor ((Y-1582)/400)-10，为简便算法，假设历元为 0 年，则自 0 年至 1582 年少算了不置闰的日数共 12 天，需加上，则计算格里历的儒略日数需减去不置闰的日数：

-floor(Y/100)+floor(Y/400)+2

最终有格里高利历转儒略日的公式：

floor(365.25*(Y+4712)) + int(30.6*(M+1)) + D - floor(Y/100)+floor(Y/400)+2 - 63.5 （M>2）

当 M<=2 时：令 Y = Y - 1，M = M + 12，可适用该公式

补充说明

（1）上式的 floor() 函数表示向下取整，而书中使用的是的 int() 函数（实际在作者写作的年代它仍表示向下取整，详见注 3），在现代编程语言中它的意义是取整，对于负数运算，如 int (-365.25) 值为 - 365 而非 366。考虑到当计算 - 4712 年 3 月 1 日之前的数据时，Y=Y-1 即 - 4713 年，对年的积日运算中出现对负数取整的情况。故将历元推到前一个置闰年即 - 4716 年以避免对负数的取整运算，此时多加了 4 年，需要在式尾中减去 1461 天。

（2）同样考虑计算机对浮点数计算精度的问题，因为计算机对十进制的表示和计算是以二进制进行的，无法得到精确值。故以 30.6001 替代 30.6 以避免出现计算误差。（原书的写作时间为上世纪 90 年代，计算精度有限，现代计算机中使用双精度浮点数，可以直接用 30.6 而不会出现计算误差。）

对此二者做出修正后，则有：

JD = floor(365.25*(Y+4716)) + int(30.6001*(M+1)) + D + B - 1524.5 （M>2）
 
当 M<=2 时：令 Y = Y - 1，M = M + 12，可适用该公式
 
对儒略历（公元前 1582 年 10 月 4 日及以前），有 B = 0
 
对格里高利历（公元前 1582 年 10 月 15 日及以后），有 B = 2 - floor(Y/100)+floor(Y/400)

但对计算机而言，该式仍然不适用于计算-4716年3月1日前的儒略日数（但可以计算从儒略日历元开始的任意一天的儒略日数）。若使用向下取整函数替换int()，则该式可使用于任意一天的儒略日计算，且不必做历元调整。

此式即可避免出现计算机取整运算与实际不一致的情况，从而避免因不同编程语言出现的计算误差。

（3）wiki 中提供了另一个公式，其实质与上式相同。[注4]

以 3 月为岁首，每 5 个月符合大小大小大的顺序，合计 153 天，平均每月 30.6 天。而计算起点为大月，需加上 0.4，取整后方得 31。故有 m 月的积日为 floor((153m+2)/5)。每年以 365 计，则需加上置闰年 floor(y/4)（365y+floor(y/4) 等价于 floor(365.25y)）。式中将历元前推到原历元上一个格里历置闰周期起点的年份 - 4800（公元前 4801 年 1 月 1 日）0 时，则需在末尾减去 (4800-4712)*365.25 即 32142 天，还需再补上 1 月和 2 月合计 59 天，得 32083 日。对格里历还需补上自 - 4712 年至 1582 年少置闰的年份，共 48 天，减去回归年过大引起的误差共 10 天。

注意这里是计算 JDN 的表达式，它与 JD 的关系是

JDN = floor(JD + 0.5)

儒略日数的计算公式还有很多，但思路类似，不再举例说明。

简化儒略日

为简化儒略日的表示，国际天文联合会决定行用简化儒略日，并定义为

MJD = JD -2400000.5

根据儒略日转公历的计算函数，可得 MJD 的的起点为儒略日 2400000.5，即公元 1858 年 11 月 17 日世界时 0 时。

儒略日计算的python实例

from datetime import *
import math
 
def ce2jd(Year,Month,D):
    if Month in [1,2]:
        M = Month + 12
        Y = Year - 1
    else:
        Y = Year
        M = Month
    B = 0
    if Y>1582 or (Y==1582 and M>10) or (Y==1582 and M==10 and D>=15):
        B = 2 - int(Y/100) + int(Y/400)  #公元1582年10月15日以后每400年减少3闰
    JD = math.floor(365.25*(Y+4716))+int(30.6*(M+1))+D+B-1524.5
    #JD = math.floor(365.25*(Y+4712))+int(30.6*(M+1))+D+B-63.5
    print("{}年{}月{}日的儒略日为：{:.5f}".format(gyjn(Year),Month,D,JD))
    if Y>1858 or (Y==1858 and M>11) or (Y==1858 and M==11 and D>=17):
        MJD = int(JD - 2400000.5)
        print("简化儒略日为：{}".format(MJD))
    return JD
 
#示例：计算当前时间的儒略日
year = datetime.now().year
month = datetime.now().month
day = datetime.now().day
ce2jd(year,month,day)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26

程序使用了一个将天文计算年份表达为公元纪年法年份的函数：

def gyjn(year):
    if year > 1:
        ce = "公元" + str(year)
    elif year == 1:
        ce = "公元元"
    elif year <= 0:
        year -= 1
        ce = "公元前" + str(-year)
    return ce

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

该程序没有对1582年10月5日至14日这失去的10日进行处理，如果输入这10日，其计算结果与10月15日至24日相同。如果需要获取用户输入，应给出相应的错误提示。

儒略日转公历

儒略日转公历即将上述表达式作为方程，进行求解。

《Astronomical Algorithms》同一章节给出了求算方法。这里分别说明每一个表达式的含义。

计算分析

1. 由于儒略日的历元为正午12时，公历历元为半夜12时，为统一计算，将儒略历历元前推至0.5日。即为：JD = JD + 0.5
2. 其中整数部分为日数，小数部分为时刻，只对整数部分进行运算。则令：

Z = floor(JD)
F = JD - Z

Z即为所求日到-4712年1月1日0时的日数。

1. 由于儒略历和格里历的岁长不同，需分别处理。即自1582年10月15日0时前适用儒略历（岁长365.25），此后适用格里历（岁长365.2425）。为统一计算，可将格里历转换为儒略历，即假设自-4712年1月1日0时起一直使用的是儒略历。则针对格里历相对儒略历少置闰（400年3闰）的部分给予补上。对于使用取整公式计算置闰，只能以一个400年置闰周期的起点为岁首，如1600年3月1日，根据儒略日计算公式，得该日的儒略日为2305507.5。

格里历除能被400整除的百年为36525日外，其余每百年仅36524日，此时分母较大，故分子每百年应增加0.25日，300年计0.75日。前对JD取整后所得Z值，仍以12时为历元，故仅需再增0.25日。

a = floor((Z - 2305507.25) / 36524.25)

再补上1582年10月4日到10月15日跳过的10天，即为自-4712年1月1日0时到所求日以儒略历计算的总积日。

A = Z + 10 + a - floor(a/4)

（注：书中a和A的表达式与此略有差异，是由于书中将历元推至公元元年1月1日，则至1582年间多置闰了12次，去除跳过的10天，共多了2日，反映在置闰公式中，相当于多计算了200年，由于在置闰公式（floor(y/100)-floor(y/400)）中，对200年间的置闰可能有2次或1次2种情况，宜推算到一次置闰周期即400年，则必然置闰3次，而多算了一次，则在表达式A中补足。即为调整儒略历和格里历的置闰误差，再次将历元从公元元年推至公元400年。这种情况思虑比较复杂，可不使用书中的表达式。）

同样地，为避免对负数取整的情况，将历元前推至-4716年3月1日0时，需补上相差的日数，合1524日。即有：

B = A + 1524

对所得的积日（儒略历），除以岁长，即为积年（表达式C），加上历元即为所求公历年份。其中整数部分为年的积日（表达式D），小数部分为月与日的积日（表达式B-D）。

C = floor((B-122.1)/365.25)

D = floor(365.25*C)

将B-D除以每月平均日数30.6为积月（表达式E），其中整数部分为月数，小数部分为日数（day）。

最后调整岁首的情况可得month和year。

宜需考虑，day的结果小于0.5时，即在上月末日，此时亦可能导致E值小于1，即在上年末月。需要分别判断处理。但也可先求JD-1日，得到正常结果，在结果上加回减去的1日即可。

已知儒略日求公历的python实例

def jd2ce(JD):
	JD = JD + 0.5  # 以BC4713年1月1日0时为历元
	Z = math.floor(JD)
	F = JD - Z  # 日的小数部分
	if Z < 2299161:  # 儒略历
		A = Z
	else:  # 格里历
		a = math.floor((Z - 2305507.25) / 36524.25)
		A = Z + 10 + a - math.floor(a/4)
	k = 0
	while True:
		B = A + 1524  # 以BC4717年3月1日0时为历元
		C = math.floor((B-122.1)/365.25)  # 积年
		D = math.floor(365.25 * C)  # 积年的日数
		E = math.floor((B-D)/30.6)  # B-D为年内积日，E即月数
		day = B - D - math.floor(30.6*E) + F
		if day >= 1: break  # 否则即在上一月，可前置一日重新计算
		A -= 1
		k += 1
	month = E - 1 if E < 14 else E - 13
	year = C - 4716 if month > 2 else C - 4715
	day += k
	if int(day) == 0: day += 1
	ce = gyjn(year)
	print("儒略日{}对应的公历日期为{}年{}月{}日".format(JD-0.5,ce,month,day),'\n')
	return year, month, day
 
# 计算示例
jd2ce(2400000.5)    # print：1858年11月17.0日（简化儒略日历元） 
jd2ce(2299160.5)    # print：1582年10月15.0日（格里历历元）
jd2ce(2299160.5-1)  # print：1582年10月4.0日（儒略历最后一日）

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31

注意：返回的 year 是天文计算年而不是公历年，如 - 1000 表示公元前 1001 年。也可以再利用上述公元纪年表达函数进行输出。

测试以上两个程序，可用以下代码：

jd2ce(ce2jd(year, month, day))

对于任意的 year,month,day，输出值与输入值相同，可以证明两个程序的正确性，不必分别测试。

时间转换

24小时制

以上计算获得的 day 含有小数，即该日的具体时间。一分钟 60 秒，一小时 3600 秒，一日 86400 秒。简单的做法是，先将小数转为秒数，整除 3600 即小时数，余数再整除 60 即分钟数。

但是，如果 day 的精度要求较高，就必须考虑每次加减乘除对不确定尾数的影响，

def day2hms(day):  # 12h起算的日数转时分秒
    day += 0.5
    d = day - math.floor(day)  # 取出一日的小数部分
    h = int(d * 24)
    m = int(round((d * 24 - h) * 60, 4))
    if m == 60:
        m = 0
        h += 1
    s = d * 86400 - h * 3600 - m * 60
    if abs(s) < 0.001: s = 0
    return h, m, round(s, 2)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

测试两个特殊日期，-1095.499999999与-1095.500000001
使用 jd2ce() 和 day2hms() 分别计算年月日和时分秒，如果使用简单方法，结果分别是 - 4715 年 1 月 1 日 0 时 0 分 0 秒和 - 4716 年 12 月 31 日 0 时 0 分 0 秒，显然二者相差应该不足 1 秒。

处理后的程序方可得到正确结果。

如果返回的 h 是 24，表示实际已经是第二天，应该将 h 改为 0，而日期多加一天。因为如开篇所言，历法的本质是积日，历法转换，通常是日的转换，而不去考虑时间。2000 年 1 月 1 日 24:00 和 2000 年 1 月 2 日 00:00 易导致不同的结果。比如在干支纪日的历法中，前者被写作戊午日，而后者是己未日。

加一天后又必须考虑月底甚至年底跨月或跨年的情况，所以应该放到前面 jd2ce () 函数中处理，方法是在该函数中判断循环退出的条件上一行（第 20 行前）增加如下代码：

hms = day2hms(F)
if hms[0] == 24: # 当夜24点，实为第二日0点
	A += 1
	F = 0
	continue

• 1
• 2
• 3
• 4
• 5

原理与前面先求JD-1日类似，这里是求JD+1日。

12 时辰制

中国古代将一天分为十二时辰，以地支命名，后又在每个时辰内各分初和正。但时辰的起点子初为 23 点并非一日的起点 24/0 点。同时，除梁实行 96 刻制及清实行 120 刻制外，一般使用的是百刻制，并不能被 12 整除。故日转为时辰时，需将一日的起点转为 23 点，且不能直接在时辰内分刻。而需从日数转为刻数，再减去已有时辰的刻数。

由于转换为时辰时起点并非跨日的24点，故而无需考虑临界情况。

dizhi = ["子","丑","寅","卯","辰","巳","午","未","申","酉","戌","亥"]
ke = ['初', '一', '二', '三', '四']
 
def day2sk(JD):  # 0h起算的日数转古时刻（百刻制）
	d = JD - math.floor(JD)  # 取出一日的小数部分（<0.0000001超过输出位数）
	chen = round(d * 12 + 0.5, 14)  # 时辰从上一日23时起
	chen_h = int(chen)
	chen_k = round(d * 100 - int(d * 12) * 100 / 12, 14)  # 该时辰内的刻数
	if chen_k < 100 / 24:
		shike = dizhi[chen_h % 12] + '正' + ke[int(chen_k)] + '刻'
	else:
		chen_k -= 100 / 24
		shike = dizhi[chen_h % 12] + '初' + ke[int(chen_k)] + '刻'
	return shike

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14

地方时

对于天文计算，其结果一般以UT为标准。如果用于中国历法的计算，需要转换为UT+8h。

亦即东八区某一日的开始即半夜0h，实际在格林尼治地方时上一日的16h。

而如果用于不同历法的转换，需注意两个历法之间的地方性。

附注

• 注1：历元即历法计算的起点。通过修改历元以简便计算是历法中的基本思想，也是本文计算的重要方法。
• 注2：Jean Meeus《Astronomical Algorithms》2nd，p59-66。
• 注3：计算机中，常用 floor() 表示向下取整函数，int() 表示取整函数。在函数内参数小于0的情况下，int() 无法代替floor() 使用。如对于 -1.5 运用两个函数进行计算，有： floor(-1.5) = -2， int(-1.5) = -1

书中使用的是 int() 函数，因为该书写作较早，使用的是BASIC语言，不区分 int() 和 floor() ，直接以 int() 作为向下取整函数。如果用现在常见的编程语言编写，仍使用该函数，易导致公式不适用于计算历元（-4716 年）前的日期。故本文在公式中改用了 floor() 函数，这在常见编程语言中自带的标准库 math 中都含有。

• 注4：https://zh.wikipedia.org/wiki/%E5%84%92%E7%95%A5%E6%97%A5
• 注5：几个类似术语辨析：

1. Julian Day：儒略日，天文中用于连续纪日的历法，历元为公元前 4713 年 1 月 1 日 12 时。
2. Julian Date（JD）：儒略日，特指某时的瞬时时刻，如 12:00:00 可能为 00 秒 - 01 秒之间或 00 秒这一时刻，此处特指后者。常转为日的小数表示。小数部分表示自某日 12 时至次日 12 时过去的日数。
3. Julian Day Number（JDN）：儒略日数。一定是整数，它表示某日距 JD 历元日相差的日数部分。可以理解为历元即公元前 4713 年 1 月 1 日 0 时。二者关系为 JDN = floor (JD+0.5)。
4. Julian Calendar：儒略历，它与儒略日实际没有直接关系。从公元前 45 年开始实施，但是早期出现过多次误闰，直至公元 8 年起确立了儒略历的一般规则。儒略历岁长为 365.25 日，平年 365 日，每 4 年置闰 1 日。
5. Gregorian Calendar：格里高利历，即现行公历。它在儒略历的基础上修正了回归年长度，历元为公元 1582 年 10 月 15 日夜半 12 时，岁长为 365.2425 日。平年 365 日，每 4 年置闰 1 日，每 400 年少闰 3 日。格里历制定时，儒略历较格里历长 10 日（儒略历在公元 3 世纪曾修正过春分日期（故 365.25-365.2425）×1300＝9.75），此 10 日在改历时被跳过，故公历中 1582 年 10 月 4 日的次日为 10 月 15 日。至今年（2018 年），已长 13 日。
6. Proleptic Julian calendar 与 Proleptic Gregorian calendar：在使用后来确定的儒略历规则以前（即公元 8 年以前），仍然使用该规则推算之前的日期，即既不依照历史误闰，也适用于表示儒略历颁行前的日期。这是方法称为逆推儒略历，较为常用。另一种是逆推格里历，即使用格里历推算格里历施行以前的日期，亦即从古到今的所有日期都使用格里历推算。由于 ISO 8601 的规范，很多计算机软件内置的日历使用了这种算法（所以会出现日期与本文计算不同的情况，判断方法是查看 1582 年 10 月有没有跳过 10 天）。另可注意的是，格里历施行后，部分国家仍继续使用了较长一段时间的儒略历。

---

公元纪年法（儒略历-格里高历）转儒略日

楼兰小石头于 2021-01-05 21:05:48 发布

一、基础知识

儒略日的计算是从公元前 4713 年 1 月 1 日平午 12:00 开始的天数积累，这是儒略日计算的起点，儒略历的规则为，分平年和闰年每 4 年一润各月份对应天数见表 1。儒略历一直使用到 1582 年 10 月 4 结束，因为存在误差改为格力高历，从 1582 年 10 月 15 日开始计算，使用格里高历，就是现在使用的公历。即公元纪年法在 1582 年 10 月 4 日及以前使用儒略历，在 1582 年 10 月 15 日及以后使用格里高历，格里高历闰年与平年月份 - 天数与儒略历一致。不同的国家使用格里高历的时间可能不一样，这个要注意，比如我们国家是新中国成立后开始使用的。

月份	1	2	3	4	5	6	7	8	9	10	11	12
天数（平年）	31	28	31	30	31	30	31	31	30	31	30	31
天数（闰年）	31	29	31	30	31	30	31	31	30	31	30	31

二、公历（天文纪年）转儒略日

2.1、儒略历转儒略日

计算儒略日就是计算年的积日 + 月的积日 + 日的积日，计算的前提为 - 4712 年 1 月 1 日以后～1582 年 10 月 4 日及以前。y 年 m 月 d 日的儒略日的计算公式为：JD=int(365.25*(y+4712)) + int(30.61*(m+1)) + d - 63.5。下面我来解释一下这个公式：

（1）首先年的积日计算，这个地方因为公元纪年法年没有公元 0 年，我们把公元前一年当做公元 0 年，这种做法叫做天文纪年法，公元前 4713 年就是 - 4712 年，y 都是以天文年来计算的。年的积日计算公式为：年的积日 = int(365.25*(y+4712)) 。细心的小伙伴会发现这个计算年的积日是有问题的，假设 y 为 - 4711 年，积年就是 - 4712 年，这个计算下来的年积日为 365 天，但由于 - 4712 年是闰年，应该是 366 天，实际计算结果比真实天数少了一天；当 y 为 - 4708 年时，积年为 - 4712、-4711、-4710、-4709 这四年，年的积日为 1461 天，这个计算结果与真实的天数一致。所以正确的年的积日计算公式为：

闰年：年的积日 = int(365.25*(y+4712))
 
平年：年的积日 = int(365.25*(y+4712)) + 1

（2）月的积日计算，在计算月的积日时我们把 2 月当做只有 28 天的时候，将 1 月、2 月当做上一年的 13、14 月，发现有以下规律（这个规律怎么来的，我也不知道，你也可以总结别的规律）：

月份 m	积日 int(30.61*(m+1)) - 63	对应的积月
3	59	1、2月
4	90	1、2、3月
5	120	1、2、3、4月
6	151	1、2、3、4、5月
7	181	1、2、3、4、5、6月
8	212	1、2、3、4、5、6、7月
9	243	1、2、3、…、7、8月
10	273	1、2、3、…8、9月
11	304	1、2、3、…9、10月
12	334	1、2、3、…10、11月
13（1月）	365	1、2、3、…11、12月
14（2月）	396	1、2、3、…12、1月

显示详细信息

那么计算月份的积日时有，月的积日 = int(30.61*(m+1)) - 63 （m>2）, 当 m<=2 是就将 m 看做前一年的 13、14 月，那么 m=m+12，这样就保证 m>2，为弥补多计算了 12 个月，年就少计算一年，所以 y=y-1。当时细心的同学会发现如果按照这种计算方法，保证 m>2 后，计算得到的 y 是闰年的话，会导致月的积日少计算一日，因为闰年 2 月为 29 天，这样的话，正确的公式应当如下：

闰年：月的积日 = int(30.61*(m+1)) - 63 + 1 （m>2）

平年：月的积日 = int(30.61*(m+1)) - 63 （m>2）

（3）日的积日计算，因为儒略日是从 - 4712 年 1 月 1 日平午 12:00 开始的天数积累，-4712 年 1 月 2 日对应的天数为 0.5 日，所以得一下公式：

日的积日 = d - 1.5

综上所述我们将上述过程画一个公式推导的流程图如下：

可以发现无论 y 是平年还是闰年，计算积日的公式均为：

JD = int(365.25*(y+4712)) + int(30.61*(m+1)) - 63 + 1 + d - 1.5   // 注意公式中 “+1” 在平年和闰年时含义的不同

• 1

化简后如下：

JD = int(365.25*(y+4712)) + int(30.61*(m+1)) + d - 63.5  // 该公式始终成立

• 1

2.2、格里高历转儒略日

（1）年的积日计算：因为格里高历每遇百年不能被 400 整除的话就不闰，按照之前年的积日计算方式就把 1582 年后百年中不需要闰的年份也闰了，所以要除掉这一部分，计算方式为：年的积日 = int(365.25*(y+4712)) - int(y/100) + int(y/400) ，但是按照这种方式计算又存在把 0 年～1582 年（应当为儒略历每四年一闰），其中每四年且为整百年的部分没有闰，没有闰的年数为 12 年（即 12 天），所以需要加上 12 天，所以年的积日计算为：

闰年：年的积日 = int(365.25*(y+4712)) - int(y/100) + int(y/400) + 12
 
平年：年的积日 = int(365.25*(y+4712)) + 1 - int(y/100) + int(y/400) + 12

（2）月的积日计算与儒略历完全一致。

（3）日的积日计算：格里高历就是目前通用的公历，是从 1582 年 10 月 15 日开始计算的，我们按照上面计算儒略历时的方法，相当于格里高历多计算了 10 天，所以要减去 10 天，所以积日的计算公式为：

日的积日 = d - 1.5 - 10

综上所述：同理格里高历转儒略日的计算公式为：

JD = int(365.25*(y+4712)) - int(y/100) + int(y/400) + 12 + int(30.61*(m+1)) - 63 + 1 + d - 1.5 -10 // 注意公式中 “+1” 在平年和闰年的含义的不同
 
化简后计算公式如下：
 
JD = int(365.25*(y+4712)) - int(y/100) + int(y/400) + int(30.61*(m+1)) + d - 61.5 // 该公式始终成立

不少文章中喜欢将格里高历计算儒略日和儒略历计算儒略日中不同的部分提取出来记作 B，B= - int(y/100) + int(y/400) + 12 -10，这一部分是由于格里高历纪年方式改变而带来的，所以仅当时间大于等于 1582 年 10 月 15 日才使用，所以格里高历转儒略日计算公式又可以写为：

B = 2 - int(y/100) + int(y/400)
 
JD = int(365.25*(y+4712)) + int(30.61*(m+1)) + B + d - 63.5 // 该公式始终成立

三、儒略日转公历（天文纪年）

3.1 儒略日转格里高历

儒略日转为格里高历（前提条件 JD>2299160.5，即 1582 年 10 月 15 日后），一般有两种思路：
①将 1582 年 10 月 15 日后当做一直使用的儒略历。
②依然将 1582 年 10 月 15 日后按照格里高历计算（这种方式要考虑你采取的计算的历元起点到 1582 年 10 月 15 日前的置闰，和格里高历不一致的地方，你的计算历元起点在 1582 年后则不用考虑）。

这里我按照第一种思路去计算转换，这是因为下面我们还会讨论计算儒略日转儒略历，这里我们直接将 JD 转为假设我们一直使用儒略历所对应的儒略日 JDr，就可以使用同样的计算规则了。假设 JD 对应的公历为 Y 年 M 月 D 日，这是格力高历所对应的日期，那么如果一直使用的儒略历要到这个 Y 年 M 月 D 日同样的日期 JDr 的值应该是多少？如果我们能得到 JD 与 JDr 的关系，那么我们可以直接使用 JDr 去计算对应的 Y、M、D。我们先贴出计算公式然后来解释它，计算公式如下：

JD = JD + 0.5 // 因为儒略日是从 - 4712 年 1 月 1 日 12 时开始计算的，我们将其往前推 0.5 日，使其从 - 4712 年 1 月 1 日 0 时开始计算，以适应我们公历日的计算
 
JD = JD + 10 // 补偿 1582 年 10 月 4 日～1582 年 10 月 15 日缺少的 10 日
 
a = int((JD - 2268993) / 36524.25)
 
//2268993 是 1500 年 3 月 1 日的儒略日 + 0.5，这个地方必须从 3 月 1 日开始计算世纪，因为这是为了算出需要补多少天，如果重 1600 年 1 月 1 日起算的话，那么 1700 年 1 月 1 日和 1700 年 3 月 1 日对应的儒略日按照
 
// 公式来看的话，都是需要补偿 1 日，但实际上 1700 年 1 月 1 日是不需要补偿的，因为 1700 年 1 月 1 日前没有经过平世纪，不需要补一天，为什么是要从 1500 年 3 月 1 日开始而不是 1600 年 3 月 1 日开始计算，
 
// 是因为计算的起点我们需要用一个闰世纪天数作为开始，1500 年 3 月 1 日～1600 年 3 月 1 日对应的天数为 36525 天，是一个闰世纪天数，1600 年 3 月 1 日～1700 年 3 月 1 日对应的天数是 36524 天是一个平世纪天
 
// 数，要想使用 “(JD - 2268993) / 36524.25” 这个式子，是不能从平世纪天数开始的。
 
JDr = JD + a - int((a+3) / 4) // 补上世纪年缺少的部分

在 1582 年 10 月 15 日前，JD 与 JDr 实际上是一致的，在这个日期之后产生的变化主要来源为，格里高历从 1582 年 10 月 4 日到 1582 年 10 月 15 日跳过了 10 日，再者是整百年不能被 400 整除的不闰，两个原因造成的，这两个原因造成的误差就是 JD 与 JDr 的关系。在按照儒略历的计算规则计算 Y 年 M 月 D 日时，是没有考虑跳过这 10 天的，所以 JDr 比实际的 JD 多 10 天，这是公式中 10 的由来。另外，格里高历整百年不能被 400 整除的不闰，而儒略历是都要闰的，所有 JDr 有多了格里高历少闰的的这几天，所以 “JDr = JD + a - int((a+3) / 4)”
上述部分就是，当 JD>2299160.5 时的计算规则，可以写成：

JD = JD + 0.5

JD = JD + 10

a = int((JD - 2268993) / 36524.25)

JD = JD + a - int((a+3) / 4) // 得到补偿后的 JD

得到补偿后的 JD，随后就完全按照儒略日转儒略历的计算规则来。下面直接介绍儒略日转儒略历的计算方法。

3.2 儒略日转儒略历

（1）年的计算：

y = int(JD/365.25) - 4712 // 这个应该比较好理解，儒略历平均年长度 365.25 天，这里提示一下 - 4712 年是 366 天，也就是计算的首年是 366 天，不做过多解释。
 
Y = y // 得到 Y，小 y 后面还有别的用处

（2）月的计算：

月的计算相对比较麻烦，记得我吗之前用于计算月的积日的公式 “int(30.61*(m+1)) - 63”，这个时候我们要倒着使用这个公式，我们先得到去掉年的积日后剩下的日数 muYD(minusYD)，这个地方仍然存在平年与闰年的区别：

muYD = JD - int(365.25*(y+4712)) - 1 // 平年
muYD = JD - int(365.25*(y+4712)) // 闰年

同样的我们要判断 muYD 是不是属于 1、2 月，因为若是 1、2 月需要看做上一年的 13、14 月，判断这个的时候有个地方要注意，有平年和闰年的区别，如下：

muYD <= 59 // 平年

muYD <= 60 // 闰年

闰年的时候也可以写作：

muYD = muYD - 1

muYD <= 59 // 判断是否为 1、2 月

并且在闰年的时候我们也需要 muYD = muYD - 1，2 月始终被当做 28 天才能使用 “int(30.61*(m+1)) - 63” 这个公式计算出正确的月份，所以综上所述求 muYD 可以写为：

muYD = JD - int(365.25*(y+4712)) - 1

并且使用 muYD <= 59 来判断是否为 1、2 月，就不用管平年还是闰年了

，若 muYD<=59，我们就要看做上一年的 13、14 月，所以：

y = y-1

muYD = JD - int(365.25*(y+4712)) - 1

再判断 muYD <= 59，若不是则可以进行下一步了

这个地方有个陷阱，“int(30.61*(m+1)) - 63” 这个公式没有理论说他是可逆的，我们需要举列说明一下它是可逆的。下面我列个与表 2 类似的表来看一下这个。

月份 M	月的积日 MD	(MD+63)/30.61 （为了方便我只保留两位小数写在下面）	int((MD+63)/30.61) - 1
3	59	3.98	2
加 1 日	4.01	3
4	90	4.99	3
加 1 日	5.03	4
5	120	5.97	4
加 1 日	6.01	5
6	151	6.99	5
加 1 日	7.02	6
7	181	7.97	6
加 1 日	8.00	7
8	212	8.89	7
加 1 日	9.01	8
9	243	9.99	8
加 1 日	10.02	9
10	273	10.97	9
加 1 日	11.00	10
11	304	11.98	10
加 1 日	12.02	11
12	334	12.96	11
加 1 日	13.00	12
13	365	13.98	12
加 1 日	14.01	13
14	396	14.99	13

显示详细信息

从上表可以看出该公式逆向使用成立。另外儒略日计算的是整日，比如说 muYD = 90，对应的就是 3 月 31 日 24:00:00，其实就是 4 月 1 日 00:00:00，没有 24:00:00 这个时刻，所以在计算正确的月份是 muYD 需要加一日，即：muYD + 1，然后再去计算。所以综上所述月份 m 的计算公式为：

muYD = JD - int(365.25*(y+4712)) - 1 // 这个地方前一个 “-1” 是指，前面说的平年年积日少减 1 天或者闰年 2 月需要当成 28 天也需要减 1 天
如果 muYD>=59，则 // 这个地方因为满 59 天时，应该是 3 月 1 日
m =(int((muYD + 1 +63)/30.61) - 1
m = m>12 ? m-12 : m
若 muYD<59，则
y = y - 1
muYD = JD - int(365.25*(y+4712)) - 1
m =(int((muYD + 1 +63)/30.61) - 1
M = m>12 ? m-12 : m // 得到月，小 m 后面还有别的用处

（3）日的计算

// 月的积日
闰年：月的积日 = int(30.61*(m+1)) - 63 + 1 （m>2）
平年：月的积日 = int(30.61*(m+1)) - 63 （m>2）

d = jd - int((y + 4712) * 365.25) - int(30.61*(m + 1)) + 63 - 1 + 1 //，小 y，小 m 这个时候用到，这个就好理解了，就是减去年的积日，和月的积日就是日了，最后面这个 + 1，是因为儒略日满前一天 24:00 实际上是第二天 0:00

上述过程画成流程图如下（左侧为不化简的，右侧为化简后的）：

四、python代码如下

#公历转儒略日
# 公历转儒略日
def myDate2JD(y: int, m: int, d: int):
	if m in [1, 2]:
		m = m + 12
		y = y - 1
	B = 0
	if y > 1582 or (y == 1582 and m > 10) or (y == 1582 and m == 10 and d >= 15):
		B = 2 - int(y / 100) + int(y / 400)
	JD = int(365.25 * (y + 4712)) + int(30.6 * (m + 1)) + d - 63.5 + B
	return JD
 
def myJD2Date(jd: float):
	"""
	儒略日转天文纪年
	:param jd: 儒略日
	:return:  年月日 时分秒
	"""
	re, jd = math.modf(jd + 0.5)
	if jd >= 2299161:  # 大于1582年10月15日
		jd = jd + 10
		a = int((jd - 2268993) / 36524.25)  # 2268993为1500年3月1日的儒略日+0.5
		jd = jd + a - int((a+3) / 4)
	y = int(jd / 365.25) - 4712
	Y = y
	while True:
		muYD = jd - int((y + 4712) * 365.25) - 1  # 除去年积日
		if muYD >= 59:
			m = int((muYD + 1 + 63) / 30.61) - 1
			M = m - 12 if m > 12 else m
			break
		else:
			y = y - 1
	D = muYD - int(30.61 * (m + 1)) + 63 + 1
	return Y, M, D

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36

包含时分秒的转换代码如下：

import math
 
def myDate2JD(y: int, m: int, d: int, hh:int = 0, mm:int = 0, ss:float = 0.0):
	"""
	将年月日转换为儒略日
	:param y: 年
	:param m: 月
	:param d: 日
	:param hh: 时
	:param mm: 分
	:param ss: 秒
	:return: 儒略日
	"""
	#日期转换
	if m in [1, 2]:
		m = m + 12
		y = y - 1
	B = 0
	if y > 1582 or (y == 1582 and m > 10) or (y == 1582 and m == 10 and d >= 15):
		B = 2 - int(y / 100) + int(y / 400)
	JD = int(365.25 * (y + 4712)) + int(30.61 * (m + 1)) + d - 63.5 + B
	JD = JD + hh/24 + mm/60/24 + ss/60/60/24
	return JD
 
def myJD2Date(jd: float):
	"""
	儒略日转天文纪年
	:param jd: 儒略日
	:return:  年月日 时分秒
	"""
	re, jd = math.modf(jd + 0.5)
	if jd >= 2299161:  # 大于1582年10月15日
		jd = jd + 10
		a = int((jd - 2268993) / 36524.25)  # 2268993为1500年3月1日的儒略日+0.5
		jd = jd + a - int((a+3) / 4)
	y = int(jd / 365.25) - 4712
	Y = y
	while True:
		muYD = jd - int((y + 4712) * 365.25) - 1  # 除去年积日
		if muYD >= 59:
			m = int((muYD + 1 + 63) / 30.61) - 1
			M = m - 12 if m > 12 else m
			break
		else:
			y = y - 1
	D = muYD - int(30.61 * (m + 1)) + 63 + 1
 
	re, hh = math.modf(re*24)
	re, mm = math.modf(re*60)
	ss = re*60
	return Y, M, D, hh, mm, ss

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51

---

python实现儒略日转公历时间

原创 LXXtime 遥感小屋

前言：

一些遥感数据或卫星测高数据的获取时间不是我们常见的‘年月日’等形式，因此再进行时间序列分析时需要转换时间。本文分享将儒略日转为公历的原理及实现。

1 预备知识 儒略日

是一个不涉及年月等概念的长期连续的记日法，在天文学，空间大地测量和卫星导航定位种经常使用。儒略日的起点定在公元前 4713 年（天文学上记为-4712 年）1 月 1 日世界时 12：00 即 JD 0 ，国际时长的 24 小时 TU24 为 1 天 即 JD 1（4713BC1 月 1 日 12：00 到 4713BC1 月 2 日 12：00）而此时儒略日的规则时 分平年和闰年 每 4 年一闰 平年 365 闰年 366 直到 1582 年 10 月 4 结束 开始用格力高历，就是现在的公历规则 每 4 年一闰， 百年不闰，400 又闰。但是格力高历其实抹掉了 10 天（1582，10 月 4 下一日直接跳到 10 月 15 日）

GPS 时：

GPS 系统内部采用的时间系统是 GPS 时间，是以 1980 年 1 月 6 日为起点,用周数（一个星期 7 天）和周数中的秒计算。

各个时间的想换转换都有严格的转换公式，其转换的主要思想是把通用时，GPS 时间转换为儒略日，然后以儒略日为媒介，实现任意两个时间系统的相互转换

儒略日的计算是从公元前 4713 年 1 月 1 日平午 12:00 开始的天数积累，这是儒略日计算的起点，儒略历的规则为，分平年和闰年每 4 年一润各月份对应天数见表 1。儒略历一直使用到 1582 年 10 月 4 结束，因为存在误差改为格力高历，从 1582 年 10 月 15 日开始计算，使用格里高历，就是现在使用的公历。即公元纪年法在 1582 年 10 月 4 日及以前使用儒略历，在 1582 年 10 月 15 日及以后使用格里高历，格里高历闰年与平年月份-天数与儒略历一致。不同的国家使用格里高历的时间可能不一样，这个要注意，比如我们国家是新中国成立后开始使用的。

2 计算分析

《Astronomical Algorithms》同一章节给出了求算方法。
本书电子版链接：

百度网盘 请输入提取码

以下是每一个表达式的含义

1. 由于儒略日的历元为正午 12 时，公历历元为半夜 12 时，为统一计算，将儒略历历元前推至 0.5 日。

即为：JD = JD + 0.5

• 1

2. 其中整数部分为日数，小数部分为时刻，只对整数部分进行运算。则令：

Z = floor(JD)F = JD - Z

• 1

Z 即为所求日到-4712 年 1 月 1 日 0 时的日数。

3. 由于儒略历和格里历的岁长不同，需分别处理。即自 1582 年 10 月 15 日 0 时前适用儒略历（岁长 365.25），此后适用格里历（岁长 365.2425）。为统一计算，可将格里历转换为儒略历，即假设自-4712 年 1 月 1 日 0 时起一直使用的是儒略历。则针对格里历相对儒略历少置闰（400 年 3 闰）的部分给予补上。对于使用取整公式计算置闰，只能以一个 400 年置闰周期的起点为岁首，如 1600 年 3 月 1 日，根据儒略日计算公式，得该日的儒略日为 2305507.5。

格里历除能被 400 整除的百年为 36525 日外，其余每百年仅 36524 日，此时分母较大，故分子每百年应增加 0.25 日，300 年计 0.75 日。前对 JD 取整后所得 Z 值，仍以 12 时为历元，故仅需再增 0.25 日。

a = floor((Z - 2305507.25) / 36524.25)

• 1

再补上 1582 年 10 月 4 日到 10 月 15 日跳过的 10 天，即为自-4712 年 1 月 1 日 0 时到所求日以儒略历计算的总积日。

A = Z + 10 + a - floor(a/4)

• 1

（注：书中 a 和 A 的表达式与此略有差异，是由于书中将历元推至公元元年 1 月 1 日，则至 1582 年间多置闰了 12 次，去除跳过的 10 天，共多了 2 日，反映在置闰公式中，相当于多计算了 200 年，由于在置闰公式（floor(y/100)-floor(y/400)）中，对 200 年间的置闰可能有 2 次或 1 次 2 种情况，宜推算到一次置闰周期即 400 年，则必然置闰 3 次，而多算了一次，则在表达式 A 中补足。即为调整"儒略历和格里历的置闰误差"以及"不识岁差和回归年过大的误差"再次将历元从公元元年推至公元 400 年。这种情况思虑比较复杂，可不使用书中的表达式。）

同样地，为避免对负数取整的情况，将历元前推至-4716 年 3 月 1 日 0 时，需补上相差的日数，合 1524 日。即有：

B = A + 1524

• 1

对所得的积日（儒略历），除以岁长，即为积年（表达式 C），加上历元即为所求公历年份。其中整数部分为年的积日（表达式 D），小数部分为月与日的积日（表达式 B-D）。

C = floor((B-122.1)/365.25)
D = floor(365.25*C)

• 1
• 2

将 B-D 除以每月平均日数 30.6 为积月（表达式 E），其中整数部分为月数，小数部分为日数（day）。

最后调整岁首的情况可得 month 和 year。

宜需考虑，day 的结果小于 0.5 时，即在上月末日，此时亦可能导致 E 值小于 1，即在上年末月。需要分别判断处理。但也可先求 JD-1 日，得到正常结果，在结果上加回减去的 1 日即可。

3 实现代码

import numpy as np

def convert_julian(JD, ASTYPE=None, FORMAT='dict'):
    # 将输入的值转换为数组，如果只有单个值，则转换为数组形式
    if (np.ndim(JD) == 0):
        JD = np.array([JD])
        SINGLE_VALUE = True
    else:
        SINGLE_VALUE = False

    JDO = np.floor(JD + 0.5)
    C = np.zeros_like(JD)
    # 计算格里历日历切换前后的C值
    IGREG = 2299161.0
    ind1, = np.nonzero(JDO < IGREG)
    C[ind1] = JDO[ind1] + 1524.0
    ind2, = np.nonzero(JDO >= IGREG)
    B = np.floor((JDO[ind2] - 1867216.25)/36524.25)
    C[ind2] = JDO[ind2] + B - np.floor(B/4.0) + 1525.0
    # 计算日期转换的系数
    D = np.floor((C - 122.1)/365.25)
    E = np.floor((365.0 * D) + np.floor(D/4.0))
    F = np.floor((C - E)/30.6001)
    # 计算日、月、年和小时
    DAY = np.floor(C - E + 0.5) - np.floor(30.6001*F)
    MONTH = F - 1.0 - 12.0*np.floor(F/14.0)
    YEAR = D - 4715.0 - np.floor((7.0+MONTH)/10.0)
    HOUR = np.floor(24.0*(JD + 0.5 - JDO))
    # 计算分钟和秒
    G = (JD + 0.5 - JDO) - HOUR/24.0
    MINUTE = np.floor(G*1440.0)
    SECOND = (G - MINUTE/1440.0) * 86400.0

    # 将所有变量转换为输出类型（从浮点数）
    if ASTYPE is not None:
        YEAR = YEAR.astype(ASTYPE)
        MONTH = MONTH.astype(ASTYPE)
        DAY = DAY.astype(ASTYPE)
        HOUR = HOUR.astype(ASTYPE)
        MINUTE = MINUTE.astype(ASTYPE)
        SECOND = SECOND.astype(ASTYPE)

    # 如果最初只导入了单个值：删除单例维度
    if SINGLE_VALUE:
        YEAR = YEAR.item(0)
        MONTH = MONTH.item(0)
        DAY = DAY.item(0)
        HOUR = HOUR.item(0)
        MINUTE = MINUTE.item(0)
        SECOND = SECOND.item(0)

    # 根据输出格式返回日期变量（默认为Python字典）
    if (FORMAT == 'dict'):
        return dict(year=YEAR, month=MONTH, day=DAY,
                    hour=HOUR, minute=MINUTE, second=SECOND)
    elif (FORMAT == 'tuple'):
        return (YEAR, MONTH, DAY, HOUR, MINUTE, SECOND)
    elif (FORMAT == 'zip'):
        return zip(YEAR, MONTH, DAY, HOUR, MINUTE, SECOND)

if __name__ == '__main__':
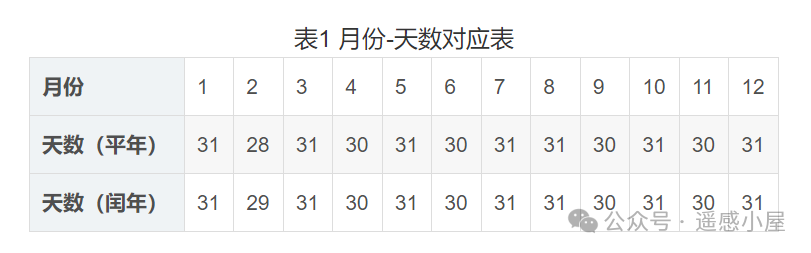
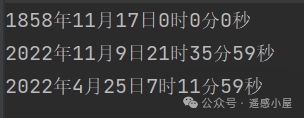
    JDs = [2400000.5, 2459893.4, 2459694.8]  # 以儒略日为例
    for JD in JDs:
        result = convert_julian(JD)
        print(f"{int(result['year'])}年{int(result['month'])}月{int(result['day'])}日"
        f"{int(result['hour'])}时{int(result['minute'])}分{int(result['second'])}秒") 

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66

输出结果：

---

历史上 “消失” 的日期：我消失了，但仿佛又没消失…

Eric 科普中国 2021 年 11 月 17 日 21:50 北京

你知道吗，1582 年的 10 月份 “凭空消失” 了 10 天，过完10 月 4 日就是10 月 15 日了。

打开手机日历，翻到 1582 年的 10 月……

真的 “消失” 了 10 天！

1582 年的 10 月到底发生了什么？

“消失” 的 10 天到底是自然选择还是人为操纵？
……

本期就让我们一探究竟……

Part 1 日期怎么就 “消失” 了？

想要弄清这 10 天 “消失” 的原因，首先我们要将自己置身于 1582 年，看看当年发生了什么。

在检索了 1582 年的大事件后，有两个条目的信息吸引了小编的眼球：

数据来源：维基百科

看来导致日期 “消失” 的 “元凶” 已经非常明显了 —— 和历法改革（儒略历 → 格里历）有关。

而后小编还发现，历史上有许多国家都进行过历法改革，但由于不同国家进行历法改革的时间不同，“消失” 的日期区间以及天数都不尽相同。

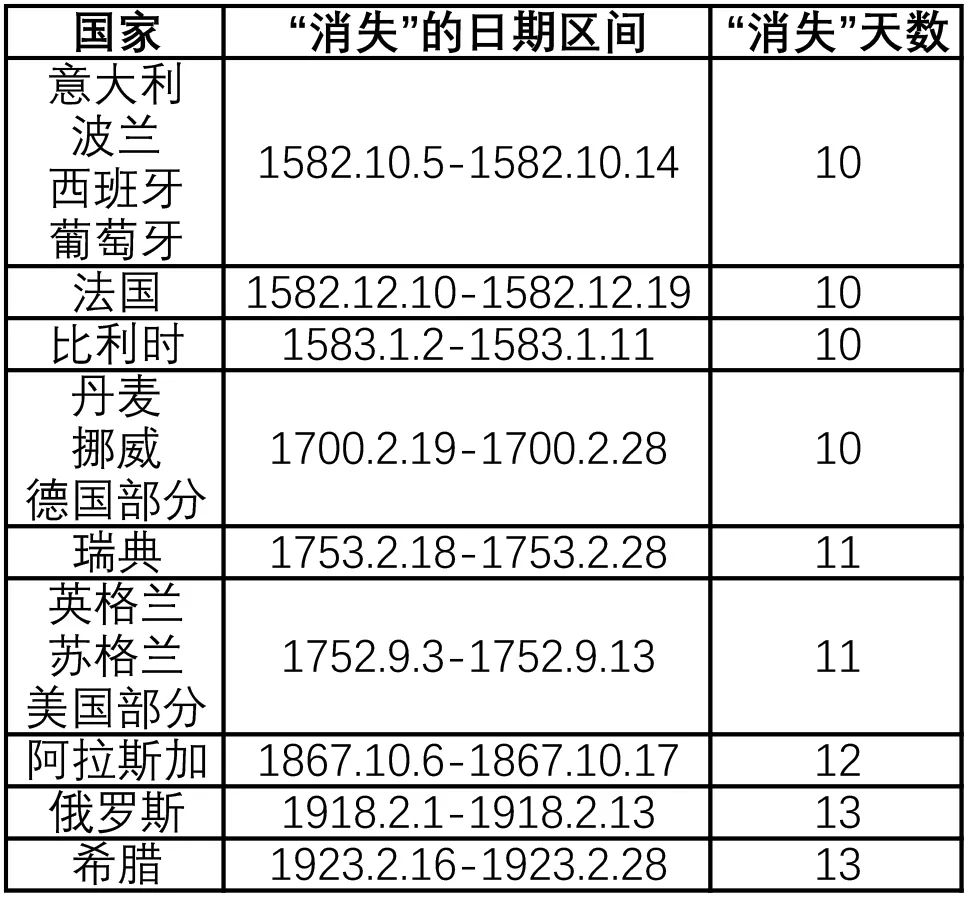
部分进行过历法改革的国家及其让日期 “消失” 的区间和天数 | 数据来源：维基百科

是什么样的契机促使一个又一个国家进行了历法改革？为什么进行历法改革的结果是让部分日期 “消失”？“消失” 的天数又是由什么决定的？

求知欲旺盛的小编决定好好扒一扒历法这件神奇的事情。

Part 2 历法知多少

历法简单来说就是用年、月、日等时间单位计算时间的方法，主要分为阳历、阴历和阴阳历三种。

阳历亦称太阳历，以每一个太阳日定义一个日期，其历年为一个回归年。当今被国际社会广泛使用的格里历（又名公历）就是阳历的一种。

阴历亦称月亮历或太阴历，以月相的变化来计算日期，其历月是一个朔望月，历年为 12 个朔望月，其大月 30 天，小月 29 天。

阴阳历的平均历年为一个回归年，历月为朔望月，因为 12 个朔望月与回归年相差太大，所以阴阳历中会设置闰月。

所以按照这样的说法，中国的农历应属于阴阳历，而非阴历。

古今中外各种历法数不胜数，今天我们就只展开说说涉及让 1582.10.5-10.14 “消失” 的两个历法 ——儒略历和格里历。

Part 3 儒略历

儒略历是由希腊数学家兼天文学家索西琴尼计算，罗马共和国独裁官儒略・凯撒颁布的历法，于公元前 45 年 1 月 1 日正式实施。

该历法将 1 年分为 12 个月，其中 1、3、5、7、9、11 月为大月（31 天），4、6、8、10、12 月为小月（30 天），唯独 2 月只有 29 天，共计 365 天。

同时该历法还规定每四年设置一个闰年，每逢闰年需要在 2 月增加一天变为 30 天，所以闰年共计 366 天。

儒略历 | 图源：52lishi

这中间还有一个小插曲，就是公元前 27 年，儒略・凯撒的继承人奥古斯都（Augustus）对儒略历进行了一些改动。

他从 2 月拿走了一天分给了 8 月（本就不富有的 2 月变得愈发贫穷），并把 9、11 月改成小月，10、12 月改成大月。

这样 2 月就只剩下 28 天（闰年 29 天），8、10、12 月每月 31 天，9、11 月每月 30 天。

相传其这么改目的只是希望自己出生的月份（8 月）是个大月……

不管怎样，在儒略历这样的规定下，我们可以算出其平均历年长度为（365×3+366）/ 4 =365.25 日，对比天文学家测量计算出的平均回归年 365.242199074 日，大约一年误差 0.0078 日，即 11 分 14 秒。

这个误差看上去并不大，但如果日积月累，量变就会引发质变，如果经过 128 年，误差就会累计到 1 天。

这样下去可不行，因为那时西方教会要根据春分（每年 3 月 21 日前后）来确定复活节，像这样每 128 年就多差 1 天的话，后面的复活节日期只会越来越早，这是不严肃的。

其实早期天文观测手段还没有那么发达的时候，人们并没有意识到这个误差会越来越大的问题，直到 16 世纪天文学家才发现，儒略历给出的日期与真实日期已有了 10 天的误差。

1582 年，时任教皇格里高利十三世决定着手解决这个问题，在综合讨论多个方案后，决定采用意大利医生兼哲学家阿洛伊修斯・里利乌斯制定的历法，并将该历法命名为格里历。

Part 4 格里历

格里历延续了儒略历大小月交替以及四年设一闰年的规则，同时又新增了一条规定：世纪年（年份为整百数）必须要被 400 整除才设为闰年，否则设为平年。

格里高利十三世与格里历 | 图源：topys

这样一来，每 400 年当中只有 97 个闰年，所以算出的平均历年长度为（365×303+366×97）/ 400 =365.2425 日。

对比平均回归年 365.242199074 日，误差仅约为每年 0.0003 日，即 25.92 秒，换句话说经过 3300 多年才会有 1 日的误差。

在当时就能将误差缩减到这个程度可以说是相当了不起了，小编估计这也是为什么格里历能一直流传至今，并且几乎被全世界使用的原因吧。

在决定使用这套历法之后，还有一个问题就是新旧历法如何衔接。

由于儒略历对应的日期相比格里历是滞后的，而平时我们常见的增加闰日（闰月）的方法只适用于日期提前的情形。

改革势在必行，但似乎又找不到一个好的方法。无奈之下，三十六计，走为上计，直接把滞后的日子删掉还不行嘛。

尽管当时这一举动引起了轩然大波，不过至少日期回归正确了，这个结果还是可以的。

Part 5 删去天数的差异

下面我们再来看看为何不同国家实施历法改革时删去的天数不同。

由于文化差异，再加上直接删除的办法实在过于大胆，许多国家根本无法一下子接受这种改革方式。

后来随着科技的日益发达，越来越多的国家发现，格里历的准确性确实经得住时间的考验，其肉眼可见的优势已然盖过了暴力删除部分日期所带来的冲击。

于是在 1582 年之后的几百年里，陆陆续续有许多国家都将旧历法更新为了格里历，同时沿用了这种删除日期以衔接两种历法的方法。

不过因为格里历规定，世纪年必须是400 的倍数才是闰年，而大多数国家的旧历法都是每 4 年一闰年。

所以在1700、1800、1900这三年里，旧历法中有 2 月 29 日，但格里历中只有 2 月 28 日。

所以只要在旧历法中多经历了一个世纪年的 2 月 29 日，在改革为格里历时就要多删去一天，所以才导致了改革晚的国家需要删去更多的天数。

---

约化儒略日新 10000 天周期开始

原创 时频基准实验室 国家授时中心 2023 年 02 月 24 日 10:04 陕西

日前，中科院国家授时中心（NTSC）和全球各国时间服务负责单位同步收到国际权度局（BIPM）时间部发送的一条提醒短文：各位同事，下周六 MJD 的数值将是 60000（注：下周六指 2023 年 2 月 25 日）。希望关注您系统的硬件和软件中发生的情况，并借此机会祝您新的 10000 天周期快乐！那么，什么是 MJD？MJD 与时间服务工作有何关系？

儒略日（Julian Day，JD）是法国学者 Joseph Justus Scaliger 设计的一种不用年和月的长期记日法，是以连续的日数计算时间的一种计时方法，主要是天文学家以及时间工作者在使用。儒略日的起点设定在公元前 4713 年（天文学上记为 -4712 年）1 月 1 日格林威治时间平午（世界时 12:00），每一天被赋予一个唯一的数字。由于儒略日数字位数太多，国际天文学联合会 IAU 于 1973 年采用约化儒略日（MJD），其定义为 MJD = JD - 2400000.5。MJD 相应的起点是 1858 年 11 月 17 日世界时 0 时。因此，MJD 是约化儒略日（Modified Julian Day，也称简化儒略日）英文首字母缩写。

目前，BIPM 时间部门以每 5 天一个数值（MJD 尾数 4 和 9）每月发布一次各国标准时间 UTC（k）与国际标准时间 UTC 的偏差，例如：MJD=59974 即 2023 年 1 月 30 日，我国标准时间 UTC（NTSC）与 UTC 的偏差为 0.8 纳秒（1 纳秒 = 0.000000001 秒）。时间需要连续计数，因此 MJD 是目前全球实际使用的标记时间最明确和有效方法。

根据计算，下一个新的 10000 天的起始，即当 MJD 等于 70000 时，将是公元 2050 年 7 月 13 日，届时将恰逢中华民族复兴伟大事业的第二个百年奋斗目标实现之际，到那时，我们将会看到一个富强民主文明和谐美丽的社会主义现代化强国。中华民族伟大复兴梦想一定能够实现！

---

以下内容来自百科

儒略历（Julian calendar），是格里历的前身，由罗马共和国独裁官儒略・凯撒采纳埃及托勒密王朝亚历山大的希腊数学家兼天文学家索西琴尼计算的历法，在公元前 45 年 1 月 1 日起执行，取代旧罗马历历法的历法。一年设 12 个月，大小月交替，四年一闰，平年 365 日，闰年于二月底增加一闰日，年平均长度为 365.25 日。该历法将罗马执政官上任的一日订为一年的开始日，即 1 月 1 日。

由于累积误差随着时间越来越大，教宗额我略十三世于 1582 年委托意大利医生兼哲学家阿洛伊修斯・里利乌斯修订历法，钦定后正式颁行，是为格里历。但大英帝国及北美十三州等直到 1752 年才停用儒略历，改用格里历。

如今包括俄罗斯正教会在内的东欧部分东方基督教社群在计算宗教节日时均仍依据传统的儒略历（如 20 世纪和 21 世纪的圣诞节在 1 月 7 日，因为其对应的正是儒略历的 12 月 25 日），除此之外只有苏格兰昔德兰群岛之富拉岛、阿索斯神权共和国和北非的柏柏尔人仍使用儒略历。

月名由来

• 一月（Januarius）：名字来自古罗马神话的神雅努斯。
• 二月（Februarius）：名字来自古罗马的节日 Februa。
• 三月（Martius）：名字来自古罗马神话的战神玛尔斯。
• 四月（Aprilis）：名字来自古罗马的词 aperire，意思为 “开始”，意味着春天开始。
• 五月（Maius）：名字来自古罗马神话的土地女神迈亚，或来自拉丁语词 maiores（意为 “较年长者”）。
• 六月（Junius）：名字来自古罗马神话的女神朱诺，或来自拉丁语词 “iuniores”（意为 “较年轻者”）。
• 七月（Julius，原名 Quintilis）：古罗马历只有 10 个月，这是第五月，原名是 “第五” 的意思。由于凯撒在该月出生，经元老院一致通过，将此月改为凯撒的名字 “儒略”。
• 八月（Augustus，原名 Sextilis）：原名是 “第六” 的意思。公元前 27 年 8 月，元老院授予屋大维 “奥古斯都”（Augustus）称号。后来罗马皇帝屋大维是死于此月，元老院将此月改为他的称号 “奥古斯都”。
• 九月（September）：拉丁语 “第七” 的意思。
• 十月（October）：拉丁语 “第八” 的意思。
• 十一月（November）：拉丁语 “第九” 的意思。
• 十二月（December）：拉丁语 “第十” 的意思。

公元前 738 年古罗马沿用古希腊历法，1 星期 = 8 日，1 个月 = 33 或 35 日（ 6 × 33 + 4 × 35），1 年 = 10 个月 = 338 日，加 Intercalaris（27 日) = 365 日。

公元前 713 年古罗马历法，Intercalaris 及 Mercedinus 合并，每两年 1 个 Intercalaris（22 日），再两年 1 个 Mercedinus（23 日），每年 = 365.25 日。

此处所谓的失闰，是调整公元前 713 年至公元前 46 年的历差至 365.2455=3 日。及至格里历在公元 1582 年颁行，明明岁差 22 日，儒略历计 365.25，是多计 12 日，但只是删除 10 日。其原因是要再公元前 713 年至公元前 46 年到 365.2425=2 日。但始终未能以 1 月 1 日成为冬至日，原因是公元前 46 年颁行儒略历是在 Mercedinus 后的第一日。

罗马失闰

因当时僧侣错误理解 “隔三年设置一闰年”，以致每三年设置了一个闰年。奥古斯都为了纠正了以上闰年过多的错误，故取消 12 年之间三次的闰年，拟补累积误差的天数。此后按儒略历原来的设计，每四年有一次闰年。

然而，此间究竟何年是平年或者闰年，不同学者之间仍然有异说，尚无定论：

学者	日期	每三年的闰年（公元前）	闰年重新开始	第一儒略日	第一调准日
可能正确的 候选解读
Scaliger	1583 年	42, 39, 36, 33, 30, 27, 24, 21, 18, 15, 12, 9	公元 8 年	公元前 45 年 1 月 2 日	公元 4 年 2 月 25 日
Bennett	2003 年	44, 41, 38, 35, 32, 29, 26, 23, 20, 17, 14, 11, 8	公元 4 年	公元前 46 年 12 月 31 日	公元前 1 年 2 月 25 日
证实 错误的 候选解读
Bünting	1590 年	45, 42, 39, 36, 33, 30, 27, 24, 21, 18, 15, 12	公元 4 年	公元前 45 年 1 月 1 日	公元前 1 年 2 月 25 日
Christmann	1590 年	43, 40, 37, 34, 31, 28, 25, 22, 19, 16, 13, 10	公元 7 年	公元前 45 年 1 月 2 日	公元 4 年 2 月 25 日
Harriot	1610 年之后	43, 40, 37, 34, 31, 28, 25, 22, 19, 16, 13, 10	公元 4 年	公元前 45 年 1 月 1 日	公元前 1 年 2 月 25 日
Kepler	1614 年	43, 40, 37, 34, 31, 28, 25, 22, 19, 16, 13, 10	公元 8 年	公元前 45 年 1 月 2 日	公元 4 年 2 月 25 日
Ideler	1825 年	45, 42, 39, 36, 33, 30, 27, 24, 21, 18, 15, 12, 9	公元 8 年	公元前 45 年 1 月 1 日	公元 4 年 2 月 25 日
Matzat	1883 年	44, 41, 38, 35, 32, 29, 26, 23, 20, 17, 14, 11	公元 4 年	公元前 45 年 1 月 1 日	公元前 1 年 2 月 25 日
Soltau	1889 年	45, 41, 38, 35, 32, 29, 26, 23, 20, 17, 14, 11	公元 8 年	公元前 45 年 1 月 2 日	公元 4 年 2 月 25 日
Radke	1960 年	45, 42, 39, 36, 33, 30, 27, 24, 21, 18, 15, 12	公元 4 年	公元前 45 年 1 月 1 日	公元前 1 年 2 月 25 日

显示详细信息

格里历与儒略历的日期差距

• 1582 年

  • 格里历 10 月 15 日，合儒略历 10 月 5 日；之后的日期：格里历日期减 10 日等于儒略历日期。

• 1583 年－1699 年：格里历日期减 10 日等于儒略历日期。

• 1700 年

  （格里历没有闰日，但儒略历有）：

  • 格里历 2 月 28 日，合儒略历 2 月 18 日；之前的日期：格里历日期减 10 日等于儒略历日期。
  • 格里历 3 月 1 日，合儒略历 2 月 19 日；之后的日期：格里历日期减 11 日等于儒略历日期。

• 1701 年－1799 年：格里历日期减 11 日等于儒略历日期。

• 1800 年

  （格里历没有闰日，但儒略历有）：

  • 格里历 2 月 28 日，合儒略历 2 月 17 日；之前的日期：格里历日期减 11 日等于儒略历日期。
  • 格里历 3 月 1 日，合儒略历 2 月 18 日；之后的日期：格里历日期减 12 日等于儒略历日期。

• 1801 年－1899 年：格里历日期减 12 日等于儒略历日期。

• 1900 年

  （格里历没有闰日，但儒略历有）：

  • 格里历 2 月 28 日，合儒略历 2 月 16 日；之前的日期：格里历日期减 12 日等于儒略历日期。
  • 格里历 3 月 1 日，合儒略历 2 月 17 日；之后的日期：格里历日期减 13 日等于儒略历日期。

• 1901 年－2099 年：格里历日期减 13 日等于儒略历日期。

• 2100 年

  （格里历没有闰日，但儒略历有）：

  • 格里历 2 月 28 日，合儒略历 2 月 15 日；之前的日期：格里历日期减 13 日等于儒略历日期。
  • 格里历 3 月 1 日，合儒略历 2 月 16 日；之后的日期：格里历日期减 14 日等于儒略历日期。

• 2101 年－2199 年：格里历日期减 14 日等于儒略历日期。

---

Other：

• 儒略日 - 卫星百科，很认真的中文航天百科 - 灰机wiki - 北京嘉闻杰诺网络科技有限公司

  https://sat.huijiwiki.com/wiki/儒略日

• 儒略日数和日干支计算器

  儒略日数和日干支计算器

---

via:

• 儒略日的由来，背景，真实的历史、演变、推算，以及在古代与现代的应用场景和具体举例_万里鸿鹄国学文化网
  https://wanlihonghu.com/儒略日的由来，背景，真实的历史、演变、推算，/

• 儒略历还是格里历？——再谈关于历史事件日期的推算与表达_江晓原_新浪博客 (2007-08-12 22:25:13)
  儒略历还是格里历？——再谈关于历史事件日期的推算与表达_江晓原_新浪博客

• 为什么孔子诞辰可以推算 --科普时报–数字报 _江晓原 2017-10-13
  为什么孔子诞辰可以推算--科普时报--数字报

• 历法的进步 —— 从牛顿的生日谈起 – 中国科学院理化技术研究所 戴闻 发布时间：2010-07-21
  历法的进步——从牛顿的生日谈起--中国科学院理化技术研究所

• 儒略日计算公式 - CSDN 博客 全都是泡饃 于 2019-07-24 07:35:55 发布
  儒略日计算公式-CSDN博客

• 儒略日与公历转换_公历转转儒略日-CSDN博客 方中 已于 2024-05-21 23:16:31 修改
  儒略日与公历转换-CSDN博客

• 公元纪年法（儒略历-格里高历）转儒略日_儒略日计算公式-CSDN博客 楼兰小石头于 2021-01-05 21:05:48 发布
  公元纪年法（儒略历-格里高历）转儒略日_儒略日计算公式-CSDN博客

• 对儒略日计算公式的解读 十八小子 2017-08-14
  儒略日计算公式的解读

• python实现儒略日转公历时间 原创 LXXtime 遥感小屋 2024年04月26日 00:00 天津
  python实现儒略日转公历时间

• 历史上 “消失” 的日期：我消失了，但仿佛又没消失… Eric 科普中国 2021 年 11 月 17 日 21:50 北京
  历史上"消失"的日期：我消失了，但仿佛又没消失…

• 约化儒略日新 10000 天周期开始 原创 时频基准实验室 国家授时中心 2023 年 02 月 24 日 10:04 陕西
  约化儒略日新10000天周期开始

儒略历由来 / 儒略日计算公式 / 历法演化-CSDN博客