每天一道ACM（三）

今天这道题叫做喷水装置，题目来源仍然是http://acm.nyist.net/JudgeOnline/problemset.php

喷水装置（一）

描述

现有一块草坪，长为20米，宽为2米，要在横中心线上放置半径为Ri的喷水装置，每个喷水装置的效果都会让以它为中心的半径为实数Ri(0<Ri<15)的圆被湿润，这有充足的喷水装置i（1<i<600)个，并且一定能把草坪全部湿润，你要做的是：选择尽量少的喷水装置，把整个草坪的全部湿润。

输入

第一行m表示有m组测试数据
每一组测试数据的第一行有一个整数数n，n表示共有n个喷水装置，随后的一行，有n个实数ri，ri表示该喷水装置能覆盖的圆的半径。

输出

输出所用装置的个数

样例输入

2
5
2 3.2 4 4.5 6 
10
1 2 3 1 2 1.2 3 1.1 1 2

样例输出

2
5

这道题在做的时候看到很多人都说，“由于题目很明显可以得出只要半径大于1的喷水装置都是可以被选中的，每个装置能够湿润草坪的有效长度为2*sqrt(r*r-1);”说实话有可能我比较愚，一时还真没反映过来这个有效长度是怎么来的（或许因为没好好读题！），直到我看到了一个百度大神的图。

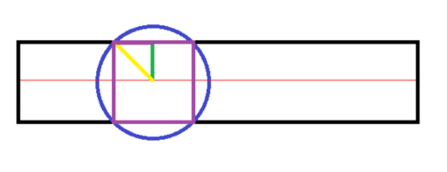
图中的紫色区域为有效区域，因为喷头喷出的是圆形，且在中心线上，所以两个喷头覆盖范围必须有所相交才能够覆盖整个矩形区域，又因为要最少的喷头数目，所以喷头有效区域要这样计算，然后相邻排放知道覆盖总共的20米才能满足题目要求。其中黄色线为半径，绿色线长度为1，这就是打什么所说的公式的由来。

由于需要最少的喷头数目，我们只需要写一个简单的贪心算法就能够实现啦。

#include<iostream>
#include<algorithm>
using namespace std;

//贪心算法

bool cmp(float a, float b)
{
	return a>b; //降序排列，如果return a<b;为升序排列
}
int main()
{   
	float *p,t;
	int testNum,n,i,sum;
	cin>>testNum;
	while(testNum--)
	{
		cin>>n;
		p=new float[n];
		for(i=0;i<n;i++)
		{
			cin>>p[i];
		}
		sort(p,p+n,cmp);
		for(i=0,sum=1,t=20;i<n;i++)
		{
			t-=2*sqrt(p[i]*p[i]-1);  //求出单个圆的实际覆盖长度后还需要覆盖多少米
			if(t<=0)
			{
				break;
			}else
			{
				sum++;
			}

		}
		cout<<sum<<endl;
		delete[] p;
	}
	return 0;
}

希望大家批评指正！