问题:根据用户输入的拼音串得到用户想要输入的语句。
隐马尔科夫模型:
可以把这个问题看做是通信问题,即拼音串是接收到的信号,目的是推测出真正的信号。这时就可以使用隐马尔科夫模型。
令
令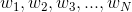
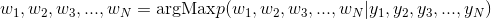
根据贝叶斯公式、独立输出假设和马尔科夫假设,上述问题可以变化为:
求使概率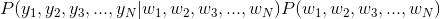
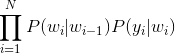
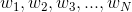
由于在拼音转汉字的问题中某个汉字对应的拼音是固定的,也就是说
问题:根据用户输入的拼音串得到用户想要输入的语句。
隐马尔科夫模型:
可以把这个问题看做是通信问题,即拼音串是接收到的信号,目的是推测出真正的信号。这时就可以使用隐马尔科夫模型。
令
令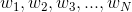
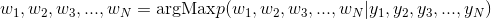
根据贝叶斯公式、独立输出假设和马尔科夫假设,上述问题可以变化为:
求使概率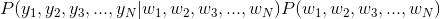
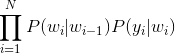
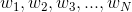
由于在拼音转汉字的问题中某个汉字对应的拼音是固定的,也就是说
 2654
2654

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


