非线性可分问题:
在分类问题中存在一种非线性可分问题,一些方法只能解决线性可分问题,如NB、LR、感知机、SVM等(K近邻是可以一种非线性模型)。解决非线性问题一般有两种思路,一是建立非线性模型(如K近邻),但是构建非线性模型一般会比较复杂;另一种思路是将特征映射到高维(甚至无穷维)的空间中,在高维空间内建立线性模型。而核方法是一种隐式建立映射的技巧,并且很容易与线性SVM结合。
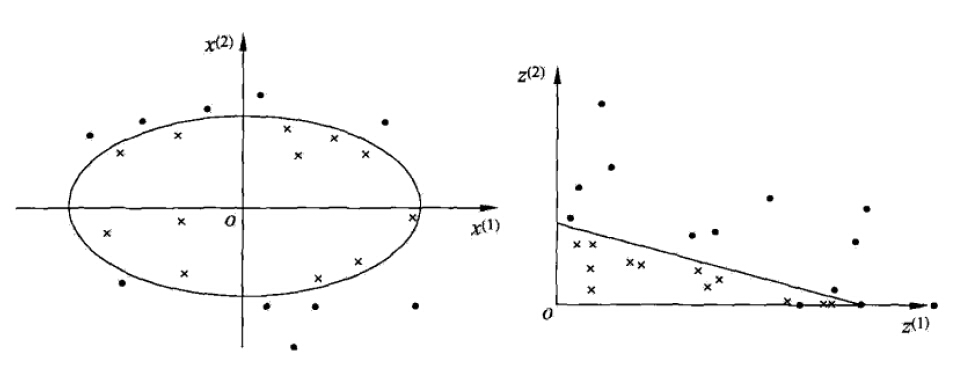
非线性可分的一个例子及映射:
上图左边显示了一个非线性可分的问题,通过映射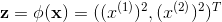
从上面的例子可以看出,找到映射函数是非线性问题转化为线性问题的关键,但是这个映射关系一般是不容易找到的,所以就出现了核方法,可以隐式的得到映射关系!
核方法:
核函数的定义为:
如果存在一个从X到H的映射,X为原特征空间,H为映射后的特征空间,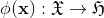
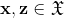
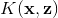
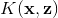
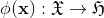
为什么核函数要定义成点积的形式呢,我觉得是因为在很多的模型中,经常会出现两个特征向量点积的形式(SVM),这使得核方法很容易可以应用到这样的模型中去。(这个解释肯定是不对的,背后一定有什么数学原理,但是目前只能理解到这个地步)
有了核函数的定义有什么好处呢?就是我们现在不需要显示的定义映射函数了!而只需要定义出核函数即可!并将原来两个特征向量点积的地方替换为核函数就可以隐式的完成映射了!
核方法在SVM中的应用:
在线性SVM的对偶问题中,无论是目标函数还是决策函数都只涉及实例与实例之间的内积。而这些内积就可以使用核函数来进行替代,从而建立非线性的SVM分类器。
非线性SVM的对偶问题的目标函数为:
分类决策函数为:
这等价于经过映射函数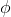

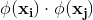
常用核函数:
1.多项式核函数:
2.高斯核函数:
3.字符串核函数:(没明白)
将上述核函数替换线性SVM中的








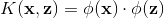
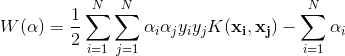
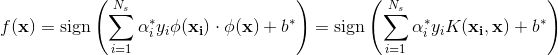
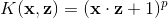
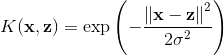

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








