HGE系列之五 管中窥豹(基础类别)
继上次我们编写了那个小程序之后,想必大家对于HGE的认识都有了进一步的提高,那么现在,我想则是时候来一番“管中窥豹”,睹一睹HGE的源码实现了 :)而相应的源码文件位于一下两个文件夹下:hge/hge181/include 和 hge/hge181/src
一. HGE的主要程序结构
还记的之前我们见过的一张HGE结构示意图吗?

图中的HGE Helper Classes 和 HGE Core Functions基本就构成了HGE的骨架,只是上图并没有涉及过多细节,更详细的类别内容自然需要参照HGE源码了:)
虽说我们这次的目的是研习HGE的源码,但这次我们也大可不必一口气将他们全部看遍,捡出其中较为简略的几个看看我想便以足矣,毕竟是刚刚开始了解HGE源码,我们大可不必操之过急,一步一步的前进,相信终有学有所成的一天,如果过于急躁,反倒是会适得其反,常言道:“欲速则不达”嘛:)
好了,不多赘言,让我们先来瞅一瞅HGE中几个比较基础的类别,我将它们皆归为base,意为起基本的支撑作用、为其他类别提供服务的一些类别,由于HGE是一款2D引擎,其base类别也相对简易,以此开始我们的代码之旅我想还是颇为恰当的:
类名:hgeRect
功能:矩形类,顾名思义,代表的是一个矩形
头文件:hge/hge181/include/hgerect.h
实现文件:hge/hge181/src/helpers/hgerect.cpp
头文件如下所列:
class hgeRect
{
public:
// 代表矩形的左上角以及右下角坐标,设置为public权限以方便访问
float x1, y1, x2, y2;
// 相对直观的构造函数,注意一下bClean这个变量
hgeRect(float _x1, float _y1, float _x2, float _y2) {x1=_x1; y1=_y1; x2=_x2; y2=_y2; bClean=false; }
hgeRect() {bClean=true;}
// 将矩形坐标内容“清空”
void Clear() {bClean=true;}
// 查询是否“清空”
bool IsClean() const {return bClean;}
// 设置矩形的坐标
void Set(float _x1, float _y1, float _x2, float _y2) { x1=_x1; x2=_x2; y1=_y1; y2=_y2; bClean=false; }
// 根据所给圆的圆心坐标及半径,设置矩形坐标
void SetRadius(float x, float y, float r) { x1=x-r; x2=x+r; y1=y-r; y2=y+r; bClean=false; }
// 根据所给坐标“裁剪”矩形
void Encapsulate(float x, float y);
// 测试所给坐标是否位于矩形内
bool TestPoint(float x, float y) const;
// 测试两个矩形是否相交
bool Intersect(const hgeRect *rect) const;
private:
bool bClean;
};
代码还是相当清晰的,相信大家根据注释已然了解了十之八九,其中值得一提,一是矩形类中设置的一个不怎么直观的bClean布尔值,其目的其实相当直观,无非是为了支持快速的清空设置和查找,是一种比较普遍的“空间”换“时间”的做法;二则是Intersect这个成员函数的实现方法:
bool hgeRect::Intersect(const hgeRect *rect) const
{
if(fabs(x1 + x2 - rect->x1 - rect->x2) < (x2 - x1 + rect->x2 - rect->x1))
if(fabs(y1 + y2 - rect->y1 - rect->y2) < (y2 - y1 + rect->y2 - rect->y1))
return true;
return false;
}
黑体加粗的两个if语句便是该函数的核心逻辑,可能一眼看去并不直观,但只要动手画张示意图,基本便可解其含义,而fabs函数的存在,自然是为了避免出现负数的情况,因为无论两个矩形想减次序为何,光就数值大小来言都是正确的,只是相差一个正负号而已:)
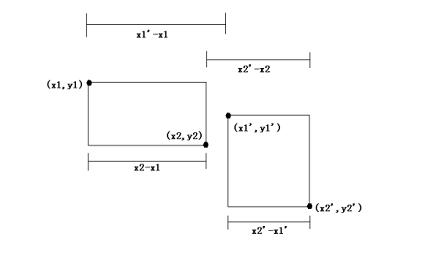
( 注:就X轴来说,两个矩形相交的充要条件即是:
abs( x1' - x1 + x2' - x2 ) < x2 -x1 + x2' - x1' ,Y轴情况类似 )
类名:hgeColorRGB&hgeColorHSV
功能:色彩类,代表一种颜色
头文件:hge/hge181/include/hgecolor.h
实现文件:无
首先,hgecolor.h文件全局定义了一个内联函数,用于裁剪颜色值至 0.0~1.0 范围:
inline void ColorClamp(float &x) { if(x<0.0f) x=0.0f; if(x>1.0f) x=1.0f; }
代码相对简易,两个条件判断而已,故而使用内联,以消除调用该函数的开销。
接着是hgeRGB的定义:
class hgeColorRGB
{
public:
// 代表Red、Green、Blue及Alpha值,定义为public属性以方便存取
float r,g,b,a;
// 相对直观的构造函数,分别传递四个相应的颜色值参数
hgeColorRGB(float _r, float _g, float _b, float _a) { r=_r; g=_g; b=_b; a=_a; }
// 直接使用一个DWORD值来构造
hgeColorRGB(DWORD col) { SetHWColor(col); }
// 缺省构造函数,四个参数皆赋值为零
hgeColorRGB() { r=g=b=a=0; }
// 自定义 减法 操作符,以支持 hgeColorRGB - hgeColorRGB 类型操作
hgeColorRGB operator- (const hgeColorRGB &c) const { return hgeColorRGB(r-c.r, g-c.g, b-c.b, a-c.a); }
// 自定义 加法 操作符,以支持 hgeColorRGB + hgeColorRGB 类型操作
hgeColorRGB operator+ (const hgeColorRGB &c) const { return hgeColorRGB(r+c.r, g+c.g, b+c.b, a+c.a); }
// 自定义 乘法 操作符,以支持 hgeColorRGB * hgeColorRGB 类型操作
hgeColorRGB operator* (const hgeColorRGB &c) const { return hgeColorRGB(r*c.r, g*c.g, b*c.b, a*c.a); }
// 自定义 自减 操作符,以支持 hgeColorRGB -= hgeColorRGB 类型操作
hgeColorRGB& operator-= (const hgeColorRGB &c) { r-=c.r; g-=c.g; b-=c.b; a-=c.a; return *this; }
// 自定义 自加 操作符,以支持 hgeColorRGB += hgeColorRGB 类型操作
hgeColorRGB& operator+= (const hgeColorRGB &c) { r+=c.r; g+=c.g; b+=c.b; a+=c.a; return *this; }
// 自定义 等号 操作符,以支持 hgeColorRGB == hgeColorRGB 类型操作
bool operator== (const hgeColorRGB &c) const { return (r==c.r && g==c.g && b==c.b && a==c.a); }
// 自定义 不等号 操作符,以支持 hgeColorRGB != hgeColorRGB 类型操作
bool operator!= (const hgeColorRGB &c) const { return (r!=c.r || g!=c.g || b!=c.b || a!=c.a); }
// 自定义 除法 操作符,以支持 hgeColorRGB / scalar 类型操作
hgeColorRGB operator/ (const float scalar) const { return hgeColorRGB(r/scalar, g/scalar, b/scalar, a/scalar); }
// 自定义 乘法 操作符,以支持 hgeColorRGB * scalar 类型操作
hgeColorRGB operator* (const float scalar) const { return hgeColorRGB(r*scalar, g*scalar, b*scalar, a*scalar); }
// 自定义 自乘 操作符,以支持 hgeColorRGB *= scalar 类型操作
hgeColorRGB& operator*= (const float scalar) { r*=scalar; g*=scalar; b*=scalar; a*=scalar; return *this; }
// 裁剪函数
void Clamp() { ColorClamp(r); ColorClamp(g); ColorClamp(b); ColorClamp(a); }
// 设置硬件颜色值(0.0~1.0范围),参数是一个DWORD,注意移位操作的使用
void SetHWColor(DWORD col) { a = (col>>24)/255.0f; r = ((col>>16) & 0xFF)/255.0f; g = ((col>>8) & 0xFF)/255.0f; b = (col & 0xFF)/255.0f; }
// 取得硬件颜色值,返回值是一个DWORD,注意移位操作的使用
DWORD GetHWColor() const { return (DWORD(a*255.0f)<<24) + (DWORD(r*255.0f)<<16) + (DWORD(g*255.0f)<<8) + DWORD(b*255.0f); }
};
// 全局定义的一个 乘法 操作符,以支持 sc * hgeColor 类型操作
inline hgeColorRGB operator* (const float sc, const hgeColorRGB &c) { return c*sc; }
至此hgeColor就已解析完毕,是不是非常简单 :)相应的hgeColorHSV的代码与hgeColorRGB大同小异,只不过换了一种颜色系(HSV)表示,有兴趣的朋友可以在相应源码文件中查看,在此我就不重复了(秉承DRY原则 :))
另外值得提到的一点是,hge文档中所谓的hgeColor实际上只是一个别名(alias)类:
#define hgeColor hgeColorRGB
不过个人感觉既然是定义类型,那么使用 typedef 更为妥当...
类名:hgeStringTable
功能:字符串表,应用于HGE的资源管理中的一个base类别
头文件:hge/hge181/include/hgestrings.h
实现文件:hge/hge181/src/helpers/hgestrings.cpp
首先来看一个定义在文件开头的结构(struct)定义:
struct NamedString
{
char name[MAXSTRNAMELENGTH];
char *string;
NamedString *next;
};
很简洁,其中的MAXSTRNAMELENGTH是一个预定义宏:
#define MAXSTRNAMELENGTH 64
所以由此来看,name这个结构成员仅仅是个普通字符数组罢了~~~大抵的作用想必也是用来存储字符而已...
而结构中*next这个自向指针的定义,让人不禁想起单链表的节点定义,如果你也是这么想的话,那么恭喜你,这是正确的直觉!这个名为NamedString的结构就是用来构成链表的!:)
那么char *string这个成员变量又是用来干什么的呢?在此我们好像还不能妄下定义,但是不用着急,我们再耐心的往下看:
class hgeStringTable
{
public:
// 构造函数,从filename文件中解析字符串
hgeStringTable(const char *filename);
~hgeStringTable();
// 获取名为name的字符串
char *GetString(const char *name);
private:
// 私有定义的拷贝构造函数,禁止拷贝构造
hgeStringTable(const hgeStringTable &);
// 私有的自定义 赋值 函数,禁止赋值操作
hgeStringTable& operator= (const hgeStringTable &);
// NamedString指针,可以认为是一个单链表头结点 :)
NamedString *strings;
// 静态HGE指针变量,用于调用HGE提供的资源加载操作
static HGE *hge;
};
先让我们看看较为简单的 ~hgeStringTable 和 GetString :
hgeStringTable::~hgeStringTable()
{
NamedString *str, *strnext;
// 将当前头结点付给str
str=strings;
// 当 str 不为空(NULL)
while(str)
{
// 获取str的下一个指向节点
strnext=str->next;
// 释放str的string内存变量
delete[] str->string;
// 释放str本身
delete str;
// 将先前暂存的下一个NamedString指针赋给str,以便进行循环操作
str=strnext;
}
// 释放hge
hge->Release();
}
代码并不出人意料,基本上便是遍历链表并释放资源,最后释放先前获取的hge,其他真的就没什么了,不过其中的delete[] str->string;这句明显表明NamedString 结构中string应该是指向一个动态分配的内存地址,看来这一点对于我们刚才的疑惑有了一点解释~~~
而GetString函数也依旧简单:
char *hgeStringTable::GetString(const char *name)
{
// 将当前头结点付给str
NamedString *str=strings;
// 当 str 不为空(NULL)
while(str)
{
// 如果name与 str->name 相同,则返回str->string
if(!strcmp(name, str->name)) return str->string;
// 否则就寻找下一个节点
str=str->next;
}
// 没有找到,便返回空
return 0;
}
好了,至此,GetString函数的原理也基本大白天下了,依旧是遍历的老套,不过对于NamedString这个之前心存困惑的结构,现在的我们应该非常清晰了:
其中的char name[MAXSTRNAMELENGTH] 代表的其实是字符串的“名字”,或者说标记,而真实的字符串内容,则毫无疑问的存储于char *string之中,最后剩下的NamedString *next也自然而然的是一个自向指针了~~~嗯~~~原来如此:)(不过资源释放的位置我感觉放的高了一些(hgeStringTable中),应该为此结构编写一个析构函数来进行处理才是)
最后,对于hgeStringTable的构造函数,由于代码较为复杂,我并不准备在这美好的第一次代码之旅便卷起袖子硬啃,而是留作下次再说,就权当悬念,大家目前只要知道其的功能是从指定文件中加载一个个命名的字符串,并串接成NamedString链表即可(如果你实在等不及,好吧,我也拦不住你,请打开相应的代码文件自己观赏...)
类名:hgeVector
功能:2D向量类
头文件:hge/hge181/include/hgevector.h
实现文件:hge/hge181/src/helpers/hgevector.cpp
向量类一般都是游戏引擎中大为有用的基础类,《3D游戏游戏编程大师技巧》的作者Andre LaMothe就说过一句名言:3D游戏就是数学,可见如向量这种隶属数学领域的基础类的重要性~~~好了,乱扯闲话到此为止,让我们马上看看今天最后一个基础类的头文件:
class hgeVector
{
public:
// 代表2D向量的x分量及y分量
float x,y;
// 相对直观的构造函数
hgeVector(float _x, float _y) { x=_x; y=_y; }
hgeVector() { x=0; y=0; }
// 自定义 取反 操作符,以支持 -hgeVector 类型操作
hgeVector operator- () const { return hgeVector(-x, -y); }
// 自定义 减法 操作符,以支持 hgeVector - hgeVector 类型操作
hgeVector operator- (const hgeVector &v) const { return hgeVector(x-v.x, y-v.y); }
// 自定义 加法 操作符,以支持 hgeVector + hgeVector 类型操作
hgeVector operator+ (const hgeVector &v) const { return hgeVector(x+v.x, y+v.y); }
// 自定义 自减 操作符,以支持 hgeVector -= hgeVector 类型操作
hgeVector& operator-= (const hgeVector &v) { x-=v.x; y-=v.y; return *this; }
// 自定义 自加 操作符,以支持 hgeVector += hgeVector 类型操作
hgeVector& operator+= (const hgeVector &v) { x+=v.x; y+=v.y; return *this; }
// 自定义 等号 操作符,以支持 hgeVector == hgeVector 类型操作
bool operator== (const hgeVector &v) const { return (x==v.x && y==v.y); }
// 自定义 不等号 操作符,以支持 hgeVector != hgeVector 类型操作
bool operator!= (const hgeVector &v) const { return (x!=v.x || y!=v.y); }
// 自定义 除法 操作符,以支持 hgeVector / scalar 类型操作
hgeVector operator/ (const float scalar) const { return hgeVector(x/scalar, y/scalar); }
// 自定义 乘法 操作符,以支持 hgeVector * scalar 类型操作
hgeVector operator* (const float scalar) const { return hgeVector(x*scalar, y*scalar); }
// 自定义 自乘 操作符,以支持 hgeVector *= scalar 类型操作
hgeVector& operator*= (const float scalar) { x*=scalar; y*=scalar; return *this; }
// 向量点乘操作
float Dot(const hgeVector *v) const { return x*v->x + y*v->y; }
// 向量长度
float Length() const { return sqrtf(Dot(this)); }
// 向量间的夹角
float Angle(const hgeVector *v = 0) const;
// 向量“裁剪”
void Clamp(const float max) { if(Length() > max) { Normalize(); x *= max; y *= max; } }
// 向量归一化
hgeVector* Normalize() { float rc=InvSqrt(Dot(this)); x*=rc; y*=rc; return this; }
// 向量旋转
hgeVector* Rotate(float a);
};
// 全局定义的 乘法 操作符,以支持 s * hgeVector 类型操作
inline hgeVector operator* (const float s, const hgeVector &v) { return v*s; }
// 全局定义的 抑或(^) 操作符,以支持 hgeVector ^ hgeVector 类型操作(向量夹角)
inline float operator^ (const hgeVector &v, const hgeVector &u) { return v.Angle(&u); }
// 全局定义的 取模(%) 操作符,以支持 hgeVector % hgeVector 类型操作(向量点乘)
inline float operator% (const hgeVector &v, const hgeVector &u) { return v.Dot(&u); }
相对来说,hgeVector的代码稍稍有些复杂,但也并没有带来太多的阅读障碍,其中对于自定义符号系的函数大多比较清晰,值得细细说一说的可能便是余下的一些成员函数:
首先我们注意到Normalize这个成员函数中,使用了一个全局函数:InvSqrt,那么这个函数的定义在哪里呢?其实在hgevector.h文件的开头,我们便能找到他:
/*
** Fast 1.0/sqrtf(float) routine
*/
float InvSqrt(float x);
很显然这是一个前向声明,通过注释我们也可以了解到这个函数的作用是快速求解1/√x,而其真正的实现则位于hgevector.cpp中:
float InvSqrt(float x)
{
union
{
int intPart;
float floatPart;
} convertor;
convertor.floatPart = x;
convertor.intPart = 0x5f3759df - (convertor.intPart >> 1);
return convertor.floatPart*(1.5f - 0.4999f*x*convertor.floatPart*convertor.floatPart);
}
代码相当晦涩难懂,由于自己对于这些数学上的优化实在没有多少研究,所以在此也不能道出个所以然来,实在抱歉了...(希望知道的朋友不吝赐教)
不过对于归一化函数(Normalize)的普通实现版本,HGE源码中也有保留,不过已经被注释掉了,我们也可以比照着看一看:
/*
hgeVector *hgeVector::Normalize()
{
float lenRcp;
lenRcp=sqrtf(Dot(this));
if(lenRcp)
{
lenRcp=1.0f/lenRcp;
x*=lenRcp;
y*=lenRcp;
}
return this;
}
*/
可以看到,正规的实现方法较之其快速版本,可读性这方面确实要大大的胜出...
接着,再来让我们看一看Angle函数的实现:
float hgeVector::Angle(const hgeVector *v) const
{
// 如果v不为空(缺省情况下v为空,见函数定义)
if(v)
{
// 使用临时变量s、v复制原向量
hgeVector s=*this, t=*v;
// 分别归一化
s.Normalize(); t.Normalize();
// 使用反三角函数求解夹角,使用了公式:
// cos(θ)= u*v/(|u||v|),,当u、v皆是单位向量时,有
// |u| =|v| = 1,则 cos(θ)= u*v,进而求解 θ
return acosf(s.Dot(&t));
}
// 否则便求解与X正轴的夹角
else return atan2f(y, x);
}
不比之前的InvSqrt,Angle函数的实现还是相当正规直接的,那么Rotate函数怎么样呢?让我们马上来瞧一下:
hgeVector *hgeVector::Rotate(float a)
{
hgeVector v;
// 使用了旋转向量公式
// x' = x*cos(θ) - y*sin(θ)
// y' = x*sin(θ) + y*cos(θ)
v.x=x*cosf(a) - y*sinf(a);
v.y=x*sinf(a) + y*cosf(a);
x=v.x; y=v.y;
return this;
}
看来依旧是非常清晰啊 :)
不过本人对于全局重载的那两个抑或(^)及取模(%)运算符的必要性则有一些不敢苟同,既然我们已经可以使用明显的函数调用来完成相应的操作,那为何还要平白的添加这么两个不直观的符号呢?hgeVector % hgeVector意为点乘~~~嗯~~~实在有些令人费解~~~
好了,乱七八糟的写了这么多,我想这第一次的HGE源码之旅也该告一段落了,而且就我个人观点,目前的篇幅确实已经有些冗长之嫌了,所以我想还是适时停笔,大家都休息一下,顺便总结一下,至于更多的HGE源码内容,就让我们下次再说吧 :)






















 4593
4593

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








