从零开始傅里叶变换

1.前言

    傅里叶变换是很多领域的基础工具，常用来做频域变换。但凭什么傅里叶变换可以转换至频域，又什么是频域。看门见山。
    连续傅里叶变换公式:
$$F(w)=<f(t),e^{iwt}>={\int }_{-\infty }^{+\infty }f(t)e^{-iwt}dt\text{\hspace{1em}(1.1)}$$
    单单看这个公式确实让人头大。还好鲁迅说过把复杂的问题拆分成各个简单的问题，解决完简单的问题，再和起来，就解决了复杂的问题。

    根据上图，我们就可得出，傅里叶变换是
        原信号$f(t)$和$e^{iwt}$的内积=$F(w)$(即原信号在角频率w上的分量)
等价于
        原信号f(t)与$e^{-iwt}$在所有时间上的积分。
我们现在这里给出最终结论：
傅里叶变换的本质就是内积，而内积的对象是由同频三角函数组成的$e^{iwt}$。通过与$e^{iwt}$的内积（投影），分离出角频率为w的分量，而${\int }_{-\infty }^{+\infty }$就是将信号每个时刻的w的分量叠加（即振幅）。
    为什么和$e^{iwt}$一参合就到频域上了。我们继续一步步拆开$e^{iwt}$看看它到底意味着什么？

2.$e^{iwt}$的秘密

2.1 从e说起

    e是自然常数，等于2.718281828459。好奇心又来了，为什么这个叫自然常数呢，这个2.71828…怎么看都不自然啊？先甩大招：
    e的定义式为：
$$\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n=e\text{\hspace{1em}(2.1.1)}$$
    公式表明当n趋于无穷大的时候$(1+\frac{1}{n}{)}^n$等于e。哦吼，这有什么特殊含义嘛？
    举个栗子，我在银行存了1元钱，年利率100%数学表达式为
$$(1+\frac{100\%}{1}{)}^1=2元$$
    但是一想，好像有点亏，我放了一年就计算一次利息，如果要是每月结一次利息就好了，利滚利就更多了，那就是
$$(1+\frac{100\%}{12}{)}^{12}=2.613元$$
    让我们更贪婪一点，要是每天算一次，每小时算一次，甚至时时刻刻都算一次，那能拿多少
$$\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n=e$$
    哦豁，就是e了。
    从每年算一次，到每时每刻算，是从离散到连续的过程。而在大千世界中，事物都是动态连续变化的，系统的此时的变量会参与到下一时刻的变化。
    式（2.11）说明一个单位状态量的变化率是固定100%的系统，e代表了在一个单位时间内，连续的翻倍增长所能达到的极限值。
    那如果变化率没那么巧，是100%呢?不妨设年利率是x，式（2.1.1）即为
$$\underset{n\to \infty }{\lim }(1+\frac{x}{n}{)}^n=\underset{n\to \infty }{\lim }（(1+\frac{1}{n/x}{)}^{n/x}{)}^x=e^x\text{\hspace{1em}(2.1.2)}$$
    由上可得，一个单位状态量的变化率是固定值的系统，其状态就可以用自然常数的指数函数来表示。
    前面我们考虑的都是单位时间，我们再把时间加入考虑范围，设时间为t，则：
$$f(t)=e^{xt}\text{\hspace{1em}(2.1.3)}$$
    哈哈哈，好了，我们发现和$e^{iwt}$是令x=iw，让我们继续往下看。

2.2 i复数的几何意义

    我们都知道$1\ast (-1)=-1；1\ast (-1)\ast (-1)=1$。引入几何学，画出下图：

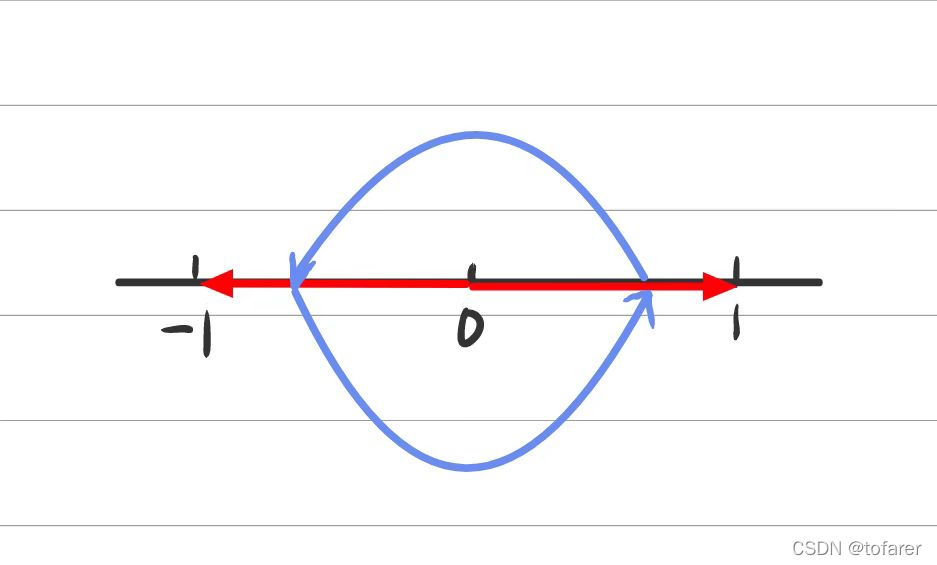
    可以发现，在上图中，*（-1）在几何中，等价于逆时针旋转180度。那好奇猫肯定要问了，如果我偏要旋转90度呢？
    旋转180度等于$\ast (-1)$为已知条件。我们设i为旋转90度需要乘的数。
即我们旋转180度，需要乘2次i，可得$1\ast i\ast i=-1$。
    化简得
$$i=\sqrt[2]{-1}\text{\hspace{1em}(2.2.1)}$$
    画图得

    如此一来，我们构建出了一个2维坐标系，好玩的就变多了。
    以前我们表达一个二维平面点需要2个数（x，y），但是现在用上i后，我们发现一个复数就可以表示一个点的位置。

    一个数表示原来2个数因此称这个数为复数。

2.3 $e^{ix}=cos(x)+isin(x)$ 欧拉！

    前面的文章我们讲到e，i这两个神奇的数字，但并未说明他们有什么关联。历史告诉我们，当世界支离破碎的时候，常常就会天降猛男。同理这时候，欧拉来了，带来了欧拉公式：
$$e^{ix}=cos(x)+isin(x)\text{\hspace{1em}(2.3.1)}$$
    关于欧拉公式通过泰勒级数的推导，可以看下面的文章
                    https://baijiahao.baidu.com/s?id=1681031751212927869&wfr=spider&for=pc
    下面通过直观的图形化过程进行讲解。
$$e^{ix}=\underset{n\to \infty }{\lim }(1+ix/n{)}^n\text{\hspace{1em}(2.3.2)}$$
    通过matlab绘制公式2.3.2图

x = 0:10:1000;			%任意值
n = 10000000000;		%n趋于无穷大
e_ix =(1+x* i./n).^n;	%计算e_ix值
compass(e_ix);			%画出罗盘图

得到

    由图可得，无论x为任何值，$e^{ix}$为单位圆（以原点为圆心，半径为1的圆）上的一点。
由此，我们可以得出下图

    同理可得，$cos(x)+isin(x)$为复平面上的一点，或者表示为以0为起点的一个向量。
    因此，傅里叶公式中的$e^{iwt}$即等价为$cos(wt)+i\ast sin(wt)$的向量，模长为1，相位为$wt$。

2.4 <>内积

    接着我们继续理解内积的意义。内积用于向量的计算，以向量$\vec{a}=(1,2),\vec{b}=(1,0)$为例：
$$<(1,2)，(1,0)>=|(1,2)|\ast |(1,0)|\ast cos(\theta )=1\ast 1+2\ast 0=1$$
    其几何含义为向量$\vec{a}$在向量$\vec{b}$上的投影，内积的结果即为系数。如果2个向量夹角为90度，则$cos(\theta )=0$,其内积为0，即2个向量正交。
    同理如果将向量扩展至n维，则其内积为
$$<\vec{a},\vec{b}>=a_1\ast b_1+a_2\ast b_2...+a_n\ast b_n=\sum _{i=1}^n(a_i\ast b_i)$$
    继续将其扩展至函数，函数是连续的，连续(即dx趋于无穷小)的累加为积分。令$a=f(x),b=g(x)$
$$<a,b>={\int }_{-\infty }^{+\infty }f(x)\ast g(x)\ast dx\text{\hspace{1em}(2.4.1)}$$
    继续扩展至复函数，$i=(-1{)}^{0.5}$,复平面上的向量$a=1+i$则
$$<a,a>=|1+i|\ast |1+1i|\ast cos(\theta )=1\ast 1-i\ast i=1\ast 1+i\ast (-i)=2$$
    由于复平面上$i=(-1{)}^{0.5}$，为了保证内积结果为正数，即保证投影的结果为正。内积计算需将虚部部分变为相减,等价于其中一个向量取共轭（$\vec{a}=1+i$取共轭为$\overline{a}=1-i$）。

    同理，推广至复函数，设a,b为复函数，则内积计算为
$$<a,b>={\int }_{-\infty }^{+\infty }f(x)\ast \overline{g(x)}\ast dx\text{\hspace{1em}(2.4.2)}$$
    因此我们设信号函数为$f(t),\overline{g(t)}=e^{iwt}$,则函数内积为
$$<f(t),e^{iwt}>={\int }_{-\infty }^{+\infty }f(t)e^{-iwt}dt\text{\hspace{1em}(2.4.3)}$$
    式2.4.2，如果大家还记得的话，就是文章开头的公式。
    我们推导得到了傅里叶变换的含义是信号$f(t)$与$e^{iwt}$的内积。2.3的部分我们得到了$e^{iwt}=cos(wt)+i\ast sin(wt)$，$e^{iwt}$是复平面上的单位向量。
    因此，傅里叶公式的直观意义就是信号$f(t)$在复平面上任一单位向量$e^{iwt}$的投影，结果为其系数。
    至此，我们关于傅里叶变换的问题变为 为什么选择在$e^{iwt}$上做投影，又为什么和频域挂上钩的？

2.5 三角函数的妙用

    三角函数($sin,cos$)是完备的正交函数集。什么意思呢？
    三角函数系为：
{ s i n ( 0 x ) , c o s ( 0 x ) , s i n ( x ) , c o s ( x ) , s i n ( 2 x ) , c o s ( 2 x ) , . . . . , s i n ( n x ) , c o s ( n x ) } \{sin(0x),cos(0x),sin(x),cos(x),sin(2x),cos(2x),....,sin(nx),cos(nx)\} {sin(0x),cos(0x),sin(x),cos(x),sin(2x),cos(2x),....,sin(nx),cos(nx)}
    完备的正交函数集的意思为在上述集合中，任选2个元素，其内积为0，即正交。比如：
$$<cos(0x),cos(x)>={\int }_{-\pi }^{\pi }cos(0x)\ast cos(x)dx={\int }_{-\pi }^{\pi }1dx+{\int }_{-\pi }^{\pi }cos(x)dx=0$$
    $sin(wt),cos(wt)$函数随着w的变化，频率发生变化。根据上述定义，可得，不同频率的三角函数内积为0，只有频率相等的三角函数做内积时，才不为0。
    通过$e^{iwt}=cos(wt)+i\ast sin(wt)$不难发现，$e^{iwt}$由同频率的三角函数相加组成。至此我们可以直观的看出，信号$f(t)$与$e^{iwt}$的内积，只有信号$f(t)$与$e^{iwt}$同频的分量才会有内积的结果，其余分量内积为0。

    傅里叶变换的本质就是内积，而内积的对象是由同频三角函数组成的$e^{iwt}$。通过与$e^{iwt}$的内积（投影），分离出角频率为w的分量，而${\int }_{-\infty }^{+\infty }$就是将信号每个时刻的w的分量叠加（即振幅）。
    通过选择不同的$e^{iwt}$便可获取信号不同的频率分量。遍历不同的频率，即形成了频谱。
    这边还有个小问题，$e^{iwt}$如何与真实的信号频率对应上呢，请看下文。

2.6 傅里叶变换的频率分析

    我们通过一个例子来进行讲解。假设我们有个连续信号$f(t)=2\ast sin(2pi\ast 66.66\ast t)+3\ast cos(2pi\ast 88.88\ast t)$
频率公式为：
$$f=1/T$$
    以$sin(2pi\ast 66.66\ast t)$为例，周期为$T=2pi/w=2pi/(2pi\ast 66.66)=1/66.66$,因此频率为$f=1/T=66.66hz$。同理可得$cos(2pi\ast 88.88\ast t)$的频率为$88.88hz$。因此该信号有66.66hz和88.88hz的信号。
    接下来进行信号的采集分析。
    首先需要设定采样频率，根据奈奎斯特采样定律，采样频率需至少为信号最高频率的2倍。为什么呢，可以直观的理解，根据傅里叶变换可知，获取信号频率的方法，是和$e^{iwt}=cos(wt)+i\ast sin(wt)$做内积，而在采样时，要确定信号最高频率的$cos(wt)，sin(wt)$的信息，至少需要确定2个点的位置。如下图。同理可得，最终得到的频谱中，有效的频率区间为采样频率的一半。

    可以通过这个单位圆来理解采样频率，和采样点数。采样频率代表$e^{iwt}$在[0，2pi]代表的频率范围，如采样频率为200HZ，即[0，2pi]对应着0-200HZ。而采样点数就是将这0-2pi分成的份数，对应的就是变换的频率。即采样频率，确定频谱的频率范围，采样点数确定频谱的刻度的精细度。比如一把10cm量程（采样频率）的尺子，最高刻度是1cm，那尺子就是将10cm等分成10份（采样点数）。

    至此，设定仿真参数为采样频率200HZ，采样点数设为100，matlab仿真代码如下：

%% 参数设置
fs=200;     %采样频率
N=100;      %采样总数
n=0:N-1;    %采样点
t=n/fs;     %采样时间间隔
%% 结果计算
y=2*sin(2*pi*66*t)+3*sin(2*pi*88*t);  %时域计算
x=fft(y,N); %傅里叶变换
m=abs(x);   %振幅取绝对值
f=n*(fs/N);   %实际频率换算
%% 绘制结果图
plot(f,m,'-*');  
xlabel('频率/Hz');ylabel('振幅');title('N=100');

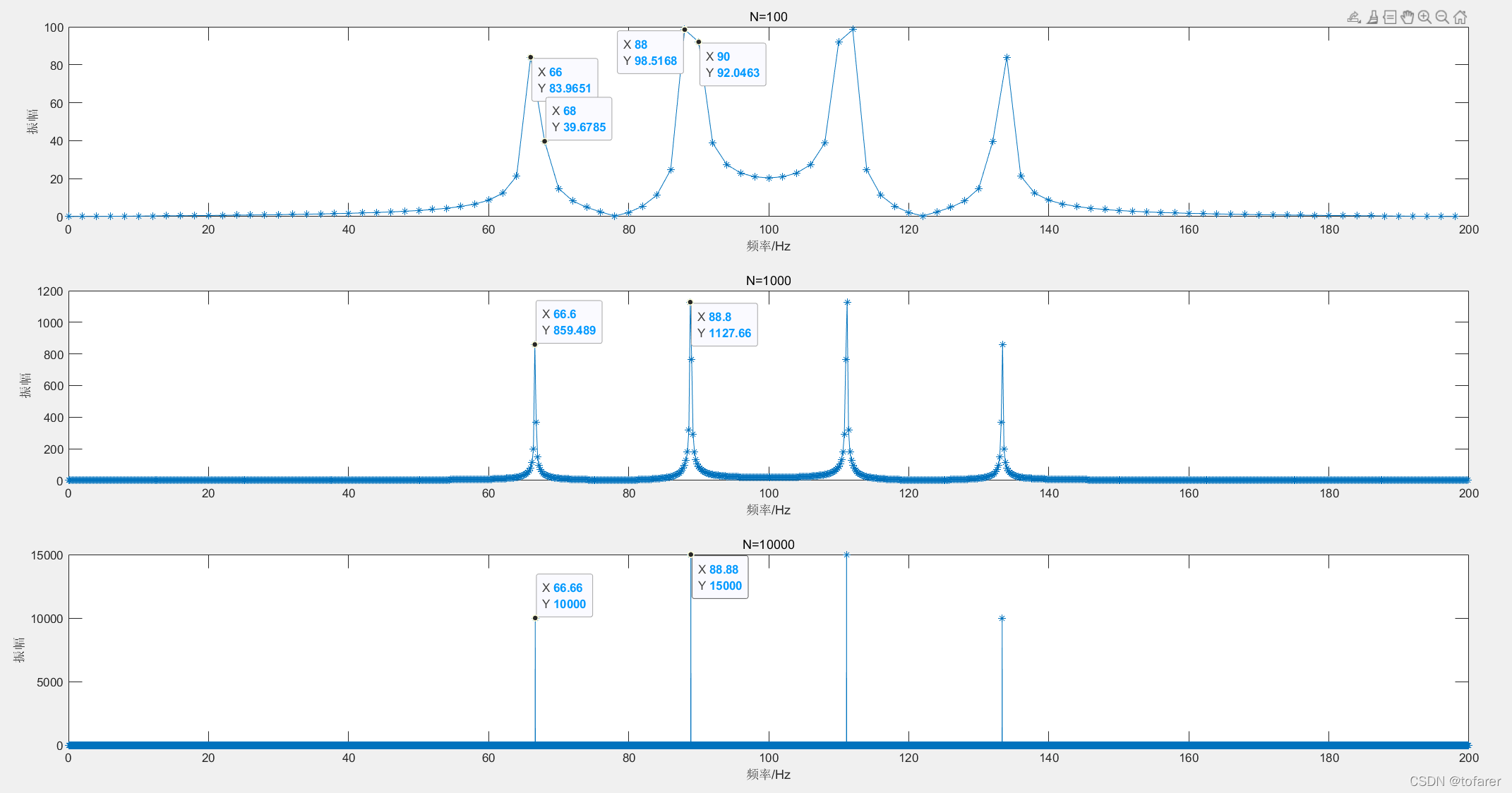
    通过仿真图就可清晰的明白采样频率，和采样点数的意义。随着采样点的增多，频谱分析逐渐精细，最终成功分辨出66.66，和88.88HZ的频率。

2.7 结语

    至此，本人已完成自己的第一篇博客。由于为了尽可能的兼顾直观和严谨，难免存在一些纰漏，希望大家不吝赐教！
    如果大家需要详细的数学推导，在此推荐B站dr_can博士的相关视频。