《面试-回溯法》 ---五种经典的算法问题

回溯法一般与递归，深度优先遍历联合使用，他的核心就是不断尝试路线，倘若碰壁（走不通）则返回到上一步进行从新试探，其程序结构分为两部分：
（1）寻找起点，并在起点位置调用探索函数。
（2）设计探索函数，每一种可能都是一种if，
其约束条件就是 探索是否超越边界and 探索位置的值是否是所需。

（1）适用范围：需要找出全部解或者最优解
（2）有组织的搜索
（3）探索解空间树

核心伪代码
方法1 使用函数内调用，则计算count需要 global 变量

def f(self,参数):
    "需要内容的布局"
    def f1(参数):
        "需要的比较复杂的条件"
    def f2(参数):
        if "跳出条件1"：
            retrun
        if "跳出条件2"：
            retrun

        "四个方向的探索"
        f2(r+1,c)
        f2(r-1,c)
        f2(r,c+1)
        f2(r,c-1)
    return '结果'

方法二：采用函数外，就是类下不同方法之间的调用。
不需要全局

class Solution():
    def Path(self,参数):
        "函数布局，产生随机矩阵，"
        # 调用同类下方法，返回所需值
        self.Find_path(参数)
        # 对所需值进行再处理
        return 结果

    def PD_K(self,参数):
    "将复杂约束条件设定"

    def Find_path(self,参数):
        "对四个位置进行探索,并对所走路径填1"
        对起始位置[0][0]设置为1
        # 如果采用方法之间的调用，则需要将将约束条件融合
        if j+1<n and self.PD_K(参数) and 标记位:
          对走过位置标记
            return self.Find_path(参数)
        elif 四个位置讨论
        else:
            return 所需结果

注意跳出条件是有顺序的

首先是大范围（矩阵边界）

其次是中等范围（特殊条件）

最后是走过的痕迹标1（不能重复）

分析见下

示例分析：
1 矩阵中的路径问题
请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。
如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。
例如 a b c e s f c s a d e e 矩阵中包含一条字符串”bcced”的路径，
但是矩阵中不包含”abcb”路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

class Solution:
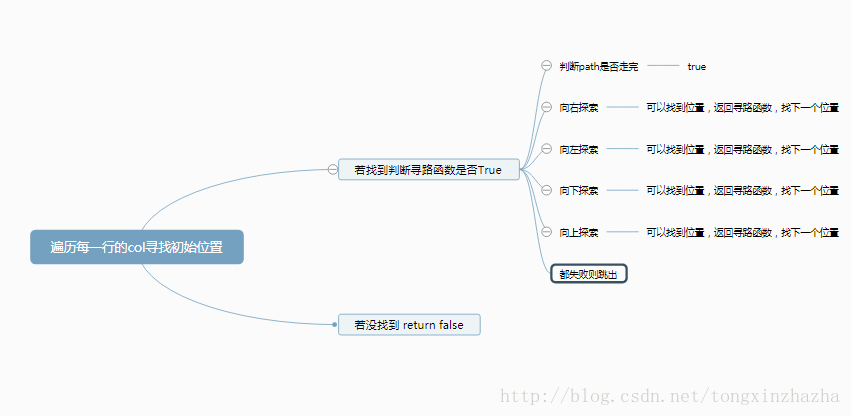
    # 函数功能：找到初始位置
    def hasPath(self, matrix, rows, cols, path):
        for i in range(rows):
            for j in range(cols):
                if matrix[i*cols+j] == path[0]:
                    if       self.find_path(list(matrix),rows,cols,path[1:],i,j):
                        return True
        #  判断这个函数是否是True, 若是则返回 True
        return False

    def find_path(self,matrix,rows,cols,path,i,j):  
    # 因为要试探，所以需要传进位置参数i,j

        if not path:  #首先判断是否全部走完
            return True
        #将走过的位置标记为0，所以前面需要将字符串矩阵改成可变对象list
        matrix[i*cols+j] = '0'   
        if j+1 >= 0 and matrix[i*cols+j+1] == path[0]:
            return self.find_path(matrix,rows,cols,path[1:],i,j+1)
        elif j+1 < cols and matrix[i*cols+j-1] == path[0]:
            return self.find_path(matrix,rows,cols,path[1:],i,j-1)
        elif i+1 < rows and matrix[(i+1)*cols+j] == path[0]:
            return self.find_path(matrix,rows,cols,path[1:],i+1,j)
        elif i-1 >= 0 and matrix[(i-1)*cols+j] == path[0]:
            return self.find_path(matrix,rows,cols,path[1:],i-1,j)
        else:
            return False

# 调用测试
_matrix = 'abcesfcsadee'
_path = 'see'
o = Solution()
print o.hasPath(_matrix, 3, 4, _path)

主要 按照 j+1 ,j-1, i+1 ,i-1的 顺序进行试探，因为本文发现，若i-1,i+1顺序改变后，试探结果失败。

实例2 机器人行走
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，
每一次只能向左，右，上，下四个方向移动一格，
但是不能进入行坐标和列坐标的数位之和大于k的格子。
例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

```
方法1
class Solution:
    def movingCount(self, threshold, rows, cols):
        "产生 0 矩阵 "
        board=[[0 for i in range(cols)] for j in range(rows)]
        global acc
        acc = 0
        "下标之和,若大于threshold则TRUE,否则Folse"
        def block(r,c):
            s=sum(map(int,str(r)+str(c)))
            return s>threshold

        def traverse(r,c):
            global acc
            if not (0<=r<rows and 0<=c<cols):   # 超出角标范围挑出
                return
            if board[r][c]!=0:    # 不等于0 跳出
                return
            if board[r][c]==-1 or block(r,c):
                board[r][c]=-1    #超出门限的点记录-1
                return

            board[r][c]=1 #符合规定的点记录1，并计数加一
            acc+=1
            traverse(r+1,c)
            traverse(r-1,c)
            traverse(r,c+1)
            traverse(r,c-1)

        traverse(0,0)
        return acc


o = Solution()
print o.movingCount(4 ,3 ,3)

方法二，使用同类下的不同方法之间调用

class Solution():
    def Path(self,m,n,k):
        "函数布局，产生随机矩阵，"
        i,j = 0,0
        count = 0
        matrix = [[0 for _ in range(n)] for _ in range(m)]
        self.Find_path(i,j,matrix,m,n,k)
        "对矩阵中的标记位置计算"
        for x in matrix:
            for y in x:
                if y == 1:
                    count +=1
        print matrix
        return count
     def PD_K(self,i,j,k):
        "确定该位置是否可以走,将复杂约束条件设定"
        index = map(str,[i,j])
        sum_ij = 0
        for x in index:
            for y in x:
                sum_ij += int(y)
        if sum_ij <= k:
            return True
        else:
            return False

    def Find_path(self,i,j,matrix,m,n,k):
        "对四个位置进行探索,并对所走路径填1"
        # 对起始位置[0][0]设置为1
        matrix[0][0] =1
        # 如果采用方法之间的调用，则需要将将约束条件融合
        if j+1<n and self.PD_K(i,j+1,k) and matrix[i][j+1]!=1:
            matrix[i][j+1] = 1
            return self.Find_path(i,j+1,matrix,m,n,k)
        elif j-1>=0 and self.PD_K(i,j-1,k) and matrix[i][j-1]!=1:
            matrix[i][j-1] = 1
            return self.Find_path(i,j-1,matrix,m,n,k)
        elif i+1< m and self.PD_K(i+1,j,k) and matrix[i+1][j]!=1:
            matrix[i+1][j] = 1
            return self.Find_path(i+1,j,matrix,m,n,k)
        elif i-1>=0 and self.PD_K(i-1,j,k) and matrix[i-1][j]!=1:
            matrix[i-1][j] = 1
            return self.Find_path(i-1,j,matrix,m,n,k)
        else:
            return matrix


m =3
n =3
k =3
o= Solution()
print o.Path(m,n,k)

讨论下遍历顺序

def traverse(r,c):
            global acc
            if matrix[i][j] ==1 :
                return
            if not (0<= i < rows and 0<= j <cols):
                return
            if PD_K(i,j,threshold):
                #matrix[i][j] = -1
                return

            board[r][c]=1 #符合规定的点记录1，并计数加一
            acc+=1
            traverse(r+1,c)
            traverse(r-1,c)
            traverse(r,c+1)
            traverse(r,c-1)

报错 if matrix[i][j] ==1 :
IndexError: list index out of range

因为先判断是是否等于1 ，再判断是否在坐标范围内，假如在矩阵右上角，先判断是否等于1时候就会报错，所以需要对if的顺序按照从大到小的顺序进行讨论。