维度的概念在数学领域和物理领域是不同的,在数学领域,维度指的是独立变量的数目,例如,三维迪卡尔坐标系由x,y,z三个独立的方向度量,也就是三组基,三个基可以表示出整个三维空间,但是基彼此又不能互相表示.在三维的基础上,还可以继续添加独立变量,所以四维乃至无限维便产生了.物理中的维度是指独立的时空坐标的数目,和时空性质有关.描述一元复变函数需要四个维度,非常遗憾的是,人眼看不到四维世界,就像一维的植物向一个方向生长,二维的蚂蚁看不到有高度的障碍物一样,我们生活的三维空间上只能看到复变函数在三维空间的投影,因此人眼无法看到复变函数的图像,因为你的眼睛看不到超过三维的东西。
在直线宇宙中,想象 不会有几何意义,因为宇宙只有一维,不会有面积
不会有几何意义,因为宇宙只有一维,不会有面积
在平面宇宙中,想象 也不会有几何意义,宇宙是个平面,没有体积.
也不会有几何意义,宇宙是个平面,没有体积.
在我们的三维世界中,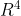 没有对应实体,宇宙是立体的,第四维是什么?物理学家认为是时间,数学家认为是任何一个独立维度,天知道?
没有对应实体,宇宙是立体的,第四维是什么?物理学家认为是时间,数学家认为是任何一个独立维度,天知道?
所以,在 中,如果
中,如果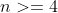 ,把
,把 想象成一个物理对象并非易事,同样的道理,
想象成一个物理对象并非易事,同样的道理, 可以看成一个平面(复平面,向量平面),但是对于
可以看成一个平面(复平面,向量平面),但是对于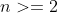 ,人类的大脑不能产生
,人类的大脑不能产生 的完整形象,不过,即便
的完整形象,不过,即便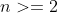 ,我们仍然可以在
,我们仍然可以在 进行代数运算,就像在线性代数
进行代数运算,就像在线性代数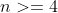 中同样容易。
中同样容易。
由此想到,代数基本定理能否这样形象化的理解一下?当你在低维空间找不到根的时候,可以转向高维空间,就像多项式
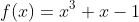
不用分析单调性,我们知道三次函数必定至少有一个实根(正,负,0都有可能),但是代数基本定理指出,它也必定存在三个根,那其余的两个根在哪里呢?
我们只能猜测,三维空间中不能存在的东西,它一定隐藏在四维空间(第四个维度不一定是时间哦,科幻小说不是理论推导).
我们先看一下函数在三维和二维空间中的图形:

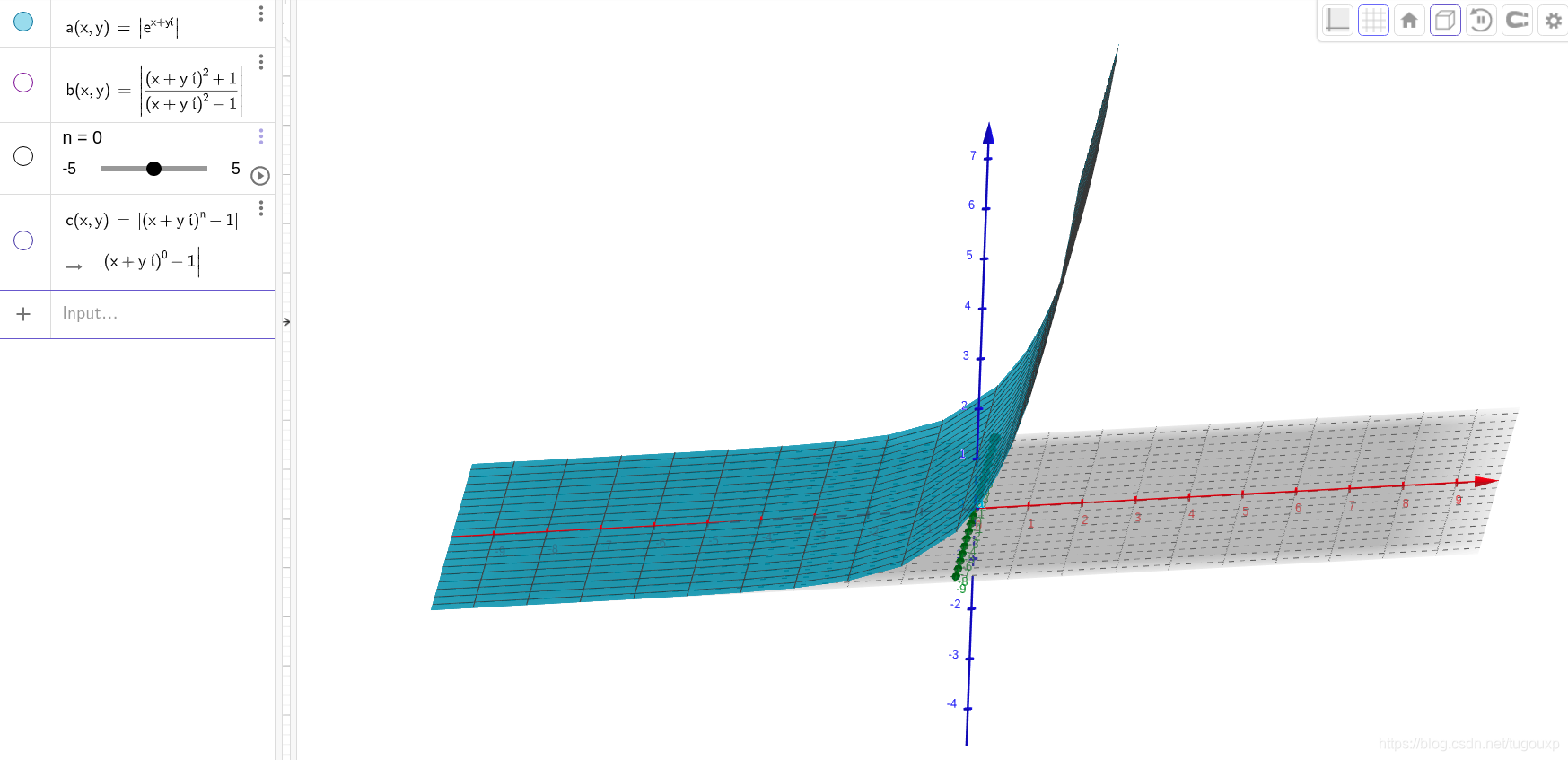
和x轴只有一个交点,所以我们的猜测是对的,方程有一个实数根,现在我们要找出它另外两个根.
令

那么:
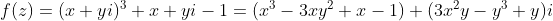
并且
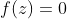
等价于:
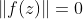
所以:
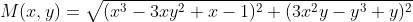
其曲面图像是:
可以看到,除了实轴上的根,其他两个根渐露真容。要知道,这里我们是采用了一个技巧才能办到的,因为模为0和方程有根等价,就是采用取模的办法,使复变函数的实部和虚部当做一个整体看待否则,这样四维空间的图像就落到了三维空间中,否则,是看不到这一图像的。
另外,一元三次方程,永远都是三个根,分两种情况:1.三个根都是实根。2.两个虚根一个实根。没有第三种情况,譬如三个虚根或者一虚两实之类的。

三次方程的根如果不是三个实根的情况(很容易构造一个三个根都是实根的三次方程),那么一定是一个实根和两个共厄虚根,并且后者的三个根一定可以在同一个圆上,当然圆心不一定是在原点,但是一定在实轴上,毕竟,三个不在同一个直线上的点共圆,结合共厄条件,很容易的出圆心位于实轴。

matlab中可以在三维空间中把实部和虚部在一个坐标系中展示出来,方法是xoy代表复平面,以z轴表示复变函数的实部,颜色表示复变函数的虚部。如下图:
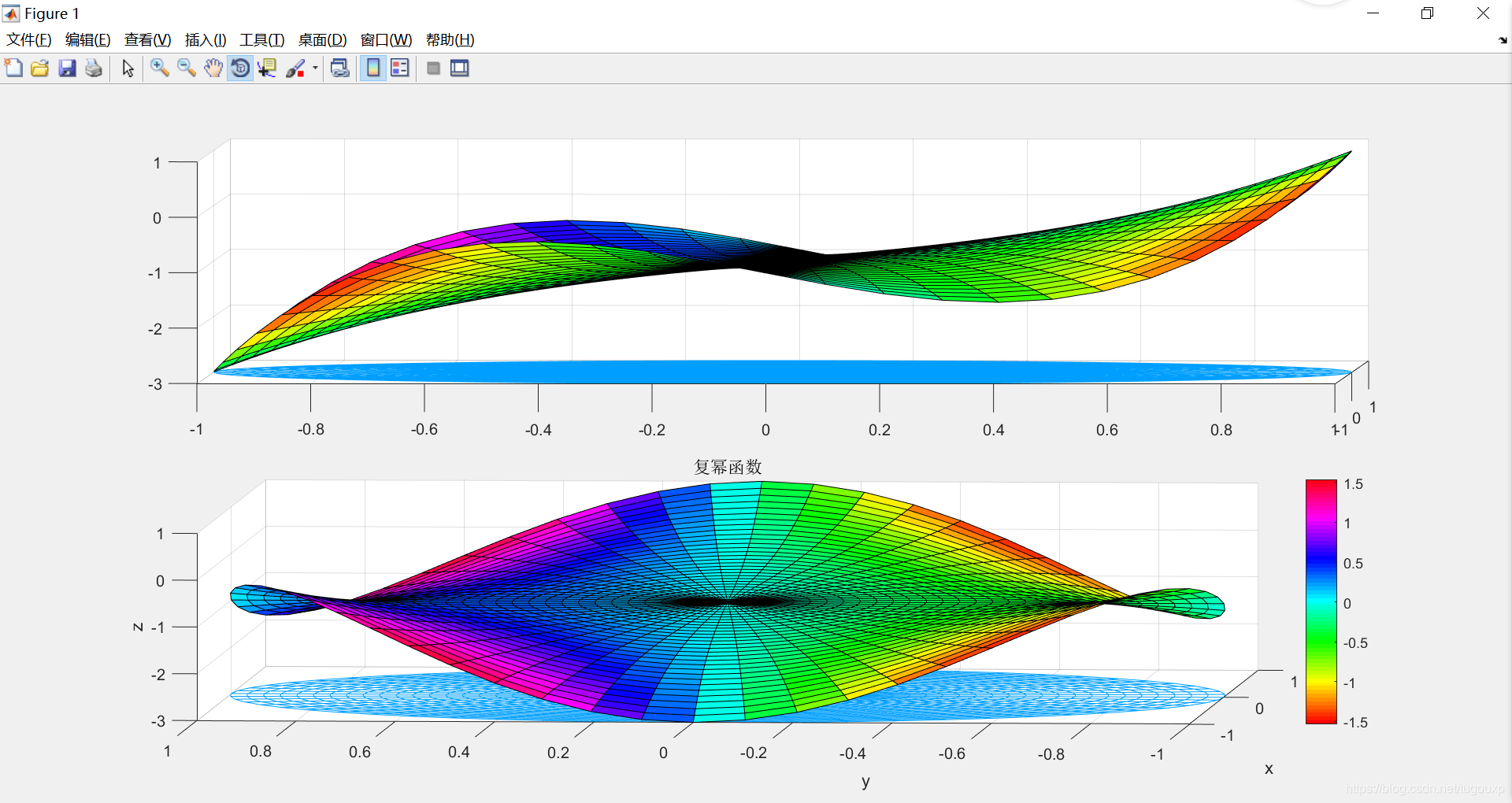
图中的颜色可不是为了好看,而是表示第四维的取值。
所以,在三维空间中无解的问题,竟然在四维空间中有解,因此你不必担心代数方程没有根,只要假定无穷维的空间存在,那么根必然存在。当然这么说很直观,也很冒险,只可以作为一条思路来辅助严格的数学证明吧!
由此引出的问题,深深震撼了我!首先世界到底是几维的?坦白讲,我完全不知道,我能看到的只是多维世界在三维世界的投影而已,所以我一辈子必将生活在捕风捉影当中,杯具!
其次如果不知道真实世界的维数,那么一切所谓科学全是建立在不靠谱的基础之上的!请原谅我如此冒昧这么对科学进行评价,因为我现在至少对科学的局限性有了点认识,不会盲目迷信科学了。
再次人眼无非是个摄像头,四维空间看不到没关系,睡觉的时候说不定就能发现自己已然处在四维空间中了,哈哈!当然不是用眼睛看到的!
又或许所有的世界级数学难题再高维空间像1+1=2那么简单,更高等的数学使用异常复杂的数学变换将计算过程引入高维空间,被赋予各种只有再高维空间存在的几何意义,达到目的后,再投影回低维空间,由于维度的缺失,投影回来的问题变得难以理解,但这一切再高维度空间不再是问题.
哎!










 博客探讨了数学和物理学中维度的不同含义,指出在三维空间基础上增加独立变量可形成更高维度。物理中的维度与时空性质相关,而数学上维度则涉及线性空间的基。文章通过代数基本定理的例子,说明在低维空间找不到解时,可以转向高维空间寻找答案,并展示了如何在四维空间中找到三维函数的额外根。尽管人眼无法直接感知高维,但高维空间在解决数学问题中的作用不容忽视。
博客探讨了数学和物理学中维度的不同含义,指出在三维空间基础上增加独立变量可形成更高维度。物理中的维度与时空性质相关,而数学上维度则涉及线性空间的基。文章通过代数基本定理的例子,说明在低维空间找不到解时,可以转向高维空间寻找答案,并展示了如何在四维空间中找到三维函数的额外根。尽管人眼无法直接感知高维,但高维空间在解决数学问题中的作用不容忽视。


















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










