证明：指数函数和阶乘谁增长的更快？

papaofdoudou

已于 2025-04-06 17:53:52 修改

阅读量7k

点赞数 7

分类专栏：数学人工智能文章标签：深度学习数学

于 2024-03-24 21:35:02 首次发布

本文链接：https://blog.csdn.net/tugouxp/article/details/136995258

版权

人工智能同时被 2 个专栏收录

155 篇文章

订阅专栏

数学

151 篇文章

订阅专栏

文章讨论了阶乘函数在增长速度上优于指数函数的现象，指出不论底数大小，指数函数无法赶上阶乘。作者还提到所有时间复杂度可转化为指数级，但在实际应用中，处理器架构限制了遇到极其复杂问题的可能性，数据结构与算法分析中的实例如排序和递归并未超出多项式时间范围。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

先说结论，阶乘增长速度比指数函数快，也就是说：

$\lim_{n \to \infty }\frac{a^n}{n!}=0$

可以用简单的指数函数y=4^x的图形和阶乘函数图形做一个对比，可以发现，在自变量取值比较小的时候，指数函数（红色）是大于阶乘的，但是当自变量取值逐渐增加时，阶乘函数后来居上，增长率和数值上远远大于了指数函数。

这个规律是不是对所有整数为底的指数函数都适用呢？不管底数多大，指数函数最终追不上阶乘函数，根据本文开头的结论，答案是肯定的。这里证明以一下：

$\boldsymbol{0\leq \frac{a^n}{n!}=\frac{a\cdot a\cdot a \cdot a \cdot \cdot a }{1\cdot 2 \cdot 3 \cdot 4 \cdot \cdot n}=\frac{a\cdot a\cdot a \cdot a \cdot \cdot a }{1\cdot 2 \cdot 3 \cdot 4 \cdot \cdot a}\times \frac{a\cdot a\cdot a \cdot a \cdot \cdot a }{(a+1)\cdot (a+2) \cdot (a+3) \cdot (a+4) \cdot \cdot n}=M\cdot \frac{a\cdot a\cdot a \cdot a \cdot \cdot a }{(a+1)\cdot (a+2) \cdot (a+3) \cdot (a+4) \cdot \cdot n}=}$

$\boldsymbol{M\cdot \frac{a\cdot a\cdot a \cdot a \cdot \cdot a }{(a+1)\cdot (a+2) \cdot (a+3) \cdot (a+4) \cdot \cdot n}=M\cdot \frac{a}{a+1}\cdot \frac{a}{a+2}\cdot \cdot \frac{a}{n}\leq M\cdot \frac{a}{n}=0}$

所以：

$\boldsymbol{0\leq \frac{a^n}{n!}\leq 0}$

根据夹逼准则：

$\boldsymbol{\lim_{n \to \infty }\frac{a^n}{n!}=0}$

结论成立。

所有的 $O(a^n)$ 时间复杂度都可以转换成指数 $O(2^n)$ 的复杂度，但是 $O(n!)$ 是一个远大于指数复杂度的算法复杂度，码农所能遇到的最复杂的实际问题应该不会比 $O(n!)$ 更复杂了，在当今的处理器架构上不具有实际意义。可能计算性分析中有理论价值，比如TSP旅行商问题的时间复杂度就是 $O(n!)$ ，实际工作中一般不与遇到这样复杂的问题，大部分算法都能在多项式时间内计算完成。

斯特林公式

当要为某些极大的n求阶乘时，直接计算的复杂度不可接受。斯特林公式（Stirling's approximation）是一条用来取n的阶乘将近似值的数学公式，它能够将求解阶乘的复杂度降低到对数级。而且，即使在n很小的时候，斯特林公式的取值已经十分准确。斯特林公式用极限表示如下：

$\boldsymbol{\lim_{n->+\infty }\frac{n!}{\sqrt{2\pi n}(\frac{n}{e})^n} = 1}$

画图表示两个函数，可以看到其曲线基本上重合：

也就是说，对于自然数n,下式成立：

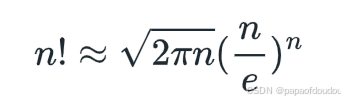
总结

在编程实践中，工程师将多项式时间作为算法可行性的分界线，也就是可以用 $O(x^k)$ 来表示的复杂度，这里k是常数。指数时间，阶乘时间是垂直的悬崖峭壁，普通人很难征服，而多项式时间虽需攀登，但终可抵达。所以，实践中通常选择一个能够在多项式时间内解决问题的算法。但是否是所有的问题都能找到多项式的复杂度呢？这个问题涉及到数学难题P=NP了，目前尚无结论。