线性代数：向量、张量、矩阵和标量

线性代数：向量、张量、矩阵和标量

背景

在线性代数中，向量、张量、矩阵和标量都属于基础概念，特别是最近AI的爆火，向量和张量的概念也越来越普及，本文将介绍下这些基本概念。

1. 标量（Scalar）

1.1 定义和表示

标量是数学中的一个基本概念，它表示一个单独的实数，没有方向。在数学表示中，我们通常用小写字母表示标量，例如 a 或 x。

1.2 例子

• 温度（32℃）
• 质量（62kg）
• 速度（102km/h）

标量是我们日常生活中常见的量，它们具有大小但没有方向。

在python代码中表示

	x = 1
	# 或者可以表示为0阶张量
    x = np.array(1)
    print(x.ndim)

2. 向量（Vector）

2.1 定义和表示

向量是有序的一维数组，向量的每个元素都是标量。每个元素都有一个索引，表示其在向量中的位置。在数学表示中，我们通常用小写粗体字母表示向量，如 v。

2.2 例子

• 位移（向东200米）
• 力（向左10牛米）

向量不仅有大小，还有方向，因此它可以表示在空间中的运动或力的作用方向。

2.3 代码和图示

一个三维向量可以表示为
$$v=\left[\begin{array}{ccc}{v}_1& v_2& v_3\end{array}\right]$$
在python代码中的例子

	v = np.array([1, 2, 3])
    print(v.ndim)  # = 1

3. 矩阵（Matrix）

3.1 定义和表示

矩阵是一个二维数组，矩阵的每个元素都是标量，这些元素按行和列排列。在数学表示中，我们通常用大写字母表示矩阵，如 A。

3.2 例子

• 图像的像素值
• 线性变换

代码和图示

一个 m x n 的矩阵 A 可以表示为：
$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$$

在python代码中例子

	m = np.array([[1, 2], [3, 4]])
    print(m.ndim)  # = 2

4. 张量（Tensor）

4.1 定义和表示

在线性代数里面可以简单的将张量理解为一个多维数组，可以包含标量、向量和矩阵。在数学表示中，我们通常用大写粗体字母表示张量，如 T

4.2 例子

• 神经网络中的输入
• 多模态数据的表示，如图片语音视频等

代码和图示

在深度学习中，一个三阶张量 T 可以用分块矩阵的方式表示：

$$\mathbf{T}=\left[\begin{array}{ccc}\mathbf{A}& \mathbf{B}& \mathbf{C}\\ \mathbf{D}& \mathbf{E}& \mathbf{F}\\ \mathbf{G}& \mathbf{H}& \mathbf{I}\end{array}\right]$$

这里A、B、C、D等可以是标量、向量或矩阵。

之间的关系

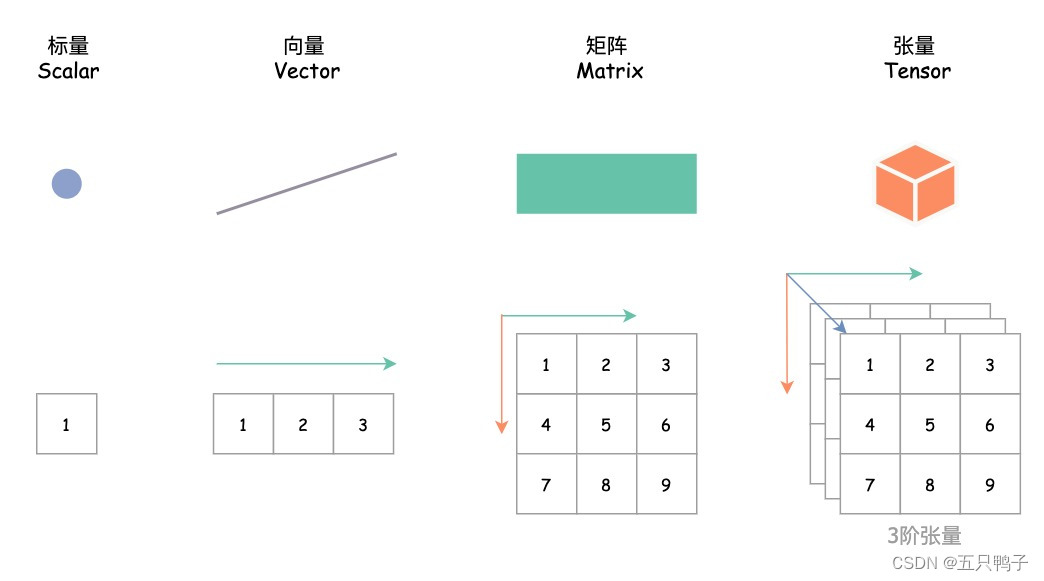
• 标量是零阶张量，向量是一阶张量，矩阵是二阶张量。
• 张量的阶数表示它包含的维度数量，不止是3阶张量，张量可以是无数阶。

在python中的例子，可以通过ndim来输出张量阶数

import numpy as np

if __name__ == '__main__':
    x = np.array(1)
    print(x.ndim)  # = 0

    v = np.array([1, 2, 3])
    print(v.ndim)  # = 1

    m = np.array([[1, 2], [3, 4]])
    print(m.ndim)  # = 2

    t = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
    print(t.ndim)  # = 3

    t = np.array([[[[1, 2], [3, 4]], [[5, 6], [7, 8]]], [[[9, 10], [11, 12]], [[13, 14], [15, 16]]],
                  [[[17, 18], [19, 20]], [[21, 22], [23, 24]]], [[[25, 26], [27, 28]], [[29, 30], [31, 32]]]])
    print(t.ndim)  # = 4

• 从这种角度来看，万物皆张量