LeetCode 5 -最长回文子串【动态规划+Manacher算法实现】

题目描述：

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

---

自己首先能想到的也就是三层循环了：

其中，第一层循环遍历所有可能的起始点；第二层循环确定所有可能的结束点；第三层循环就是依据第一、二次循环所得的起始点和结束点来判断对应字符串是不是回文子串。

可以很明显知道，这种方法时间复杂度太大：O(n^3)

//暴力方法，时间复杂度O(n^3)
    public static String longestPalindrome(String s) {
        if (s.length() == 0) {//空字符串
            return "";
        }
        if (s.length() == 1) {//只含有一个字符的字符串
            return s;
        }
        int len = 1;//此时的字符串长度至少为2，所以此时字符串包含的回文子串长度至少为1
        int start = 0;//记录最长回文子串的开始位置
        for (int i = 0; i < s.length(); i++) {
            for (int j = i + 1; j < s.length(); j++) {//从第i+1个字符开始遍历判断
                int left, right;
                for (left = i, right = j; left < right; left++, right--) {//left++从前往后，right--从后往前，如果中途出现不相等的字符，说明i到j之间的字符串一定不是回文子串
                    if (s.charAt(left) != s.charAt(right)) {
                        break;
                    }
                }
                if (left >= right && (j - i + 1) > len) {//如果left>=right说明i到j之间的字符串是回文子串，再加上(j-i+1)>len表明此时的回文子串是目前来说最长的回文子串
                    len = j - i + 1;//记录目前来说最长的回文子串的长度
                    start = i;//记录目前来说最长的回文子串的开始位置
                }
            }
        }
        return s.substring(start, len + start); //左闭右开，表示从start位置开始截取，截取长度为len   注：substring()函数的第一个参数表示截取开始下标，第二个参数表示截取结束下标
    }

---

那么接下来说一种可以将求解方法变成O(n^2)的方法：

动态规划求解

对于所给的字符串s，假设dp[i][j]=true表示字符串s[i...j]是回文子串，那么dp[i+1...j-1]必定也为true。则求解最长回文子串就可以分解成一系列子问题，并通过动态规划来求解了。

状态转移方程：

上述状态转移方程表示，

当s[i]==s[j]时，如果s[i+1...j-1]是回文子串，则s[i...j]也是回文子串；如果s[i+1...j-1]不是回文子串，则s[i...j]也不是回文子串

当s[i]!=s[j]时，字符串s[i...j]一定不是回文子串

那么由于单个字符，以及两个相邻且相同字符一定是回文子串，所以可得初始状态为：

• dp[i][i]=1
• dp[i][i+1]=1 if s[i]==s[i+1]

//动态规划求解 DP ，时间复杂度O(n^2)
    private static String longestPalindrome(String s) {
        if (s == null || s.length() == 0) {
            return "";
        }
        int len = s.length();
        boolean[][] F = new boolean[len][len];
        int maxLen = 0;
        int start = 0;
        int end = 0;
        //上三角形：只更新一半
        // 从最后一行的最后一个元素开始，往前更新
        for (int i = len - 1; i >= 0; i--) {
            for (int j = i; j < len; j++) {
                if (j == i) {
                    F[i][j] = true;
                } else if (j == i + 1) {
                    F[i][j] = s.charAt(i) == s.charAt(j);
                } else {
                    F[i][j] = F[i + 1][j - 1] && s.charAt(i) == s.charAt(j);
                }
                if (F[i][j] && maxLen < j - i + 1) {
                    start = i;
                    end = j;
                    maxLen = j - i + 1;
                }
            }
        }
        return s.substring(start, end + 1);
    }

接下来介绍的Manacher算法求解最长回文子串可以将时间复杂度降到O(n)

Manacher算法

由于给定字符串长度可奇可偶，所以为了方便统一处理，我们给字符串每个字符的左右两边都加上一个特殊字符，如#

例：level【长度5】  ->  #l#e#v#e#l#  【长度11】

例：noon【长度4】  -> #n#o#o#n#  【长度9】

---

对于加上了特殊字符后所得的字符串ns，我们可以得到跟字符串ns对应的等长数组p，其中p[i]表示以ns中第i个字符为中心所得的回文子串的半径，如果p[i]=1，表示这个回文子串就是ns中第i个字符本身【单个字符也是回文子串】

字符串ns：  #  1  #  2  #  2  #  1  #  2  #  2  #

对应数组p：1  2  1  2  5  2  1  6  1  2  3  2  1

在得到数组p之后，我们就可以知道以每个字符为中心所得的回文子串的长度：以上面"#1#2#2#1#2#2#"字符串为例，以第二个1为中心的回文子串"#2#2#1#2#2#"的半径是6，而未添加#号的回文子串"22122"的长度是5，为半径-1。再以字符串"#l#e#v#e#l#"为例，以v为中心的回文子串"#l#e#v#e#l#"的半径为6，而未加#号的回文子串"level"的长度是5，也是半径-1。再以字符串"#n#o#o#n#"为例，以中间的#号为中心的回文子串"#n#o#o#n#"的半径为5，而未加#号的回文子串"noon"的长度是4，也为半径-1。所以我们可以知道的是只要我们找到了最大的半径，我们就可以知道最长回文子串的长度：最大半径-1。但是只知道长度，不知道起始位置也无济于事，所以接下来我们来看看如何找起始位置。

还是以字符串"#1#2#2#1#2#2#"为例，第二个1的位置为7，而半径为6, 7-6=1刚好就是回文子串"22122"在"122122"中的起始位置。那么是不是最长回文子串的中心位置减去半径长度就可以得到最长回文子串在原给定子串s中的起始位置呢？就是再看字符串"#l#e#v#e#l#"，字符v的位置为5，半径为6, 5-6为负数显然不对。而将中心向后移动一位后再减去半径得0，所以我们需要在字符串前增加一个特殊字符，该字符不能是#，也不能是原给定字符串s中出现的字符，这里暂时用$【新增加的字符与原字符都不同则不会更改p数组】。那么此时v在字符串"$#l#e#v#e#l#"中的位置就是6，半径为6， 6-6等于0。那么在加了一个字符后对原来的字符串"$#1#2#2#1#2#2#"有没有影响呢？我们来验证一下，此时第二个1的位置变成了8，半径为6， 8-6得2，而我们需要的是1，所以给所得结果除以2后可得1。而对于字符串"$#l#e#v#e#l#"，由于字符v的位置为6，半径为6 ，两数相减后结果为0，除以2还是0，所以没有影响。接着我们可以在验证一下字符串"$#n#o#o#n#"，中间的#所在位置是5，半径为5，相减后除以2是0，恰好也是回文子串"noon"在原字符串"noon"的起始位置。所以我们可以得出的结论是：最长回文子串在原字符串中的起始位置为半径最长的回文子串的中心的位置减去半径后再除以2。

---

接下来我们来看看如何求数组p。增加两个辅助变量mx和id，其中

id用来记录目前已经求得的以每个字符为中心，能延伸到目前来说最往右的回文子串的中心的位置（下标）

mx用来记录以id为中心p[id]为半径的那个回文子串的最右边字符的下一个字符所在的位置（下标）

则p[i]=(mx > i) ? Math.min( p[2*id - 1],mx - i ) : 1

---

如果mx > i ，则说明c[i]在以c[id]为中心，p[id]为半径的回文子串中，我们可以找到字符c[i]的对称字符c[j]。

                       如果mx-i > p[j]，说明以c[j]为中心的回文子串包含在以c[id]为中心的回文子串中，由对称性知，则以c[i]为中心的回文子串一定也包含在以c[id]为中心的回文子串，且以c[i]为中心的回文子串的半径等于以c[j]为中心的回文子串的半径，即p[i]=p[j]

                      如果mx-i <= p[j]，则说明以c[j]为中心的回文子串不一定包含在以c[id]为中心的回文子串中，那么此时以c[i]为中心的回文子串的半径至少是mx-i。对于超出mx的部分，我们需要自己匹配确认

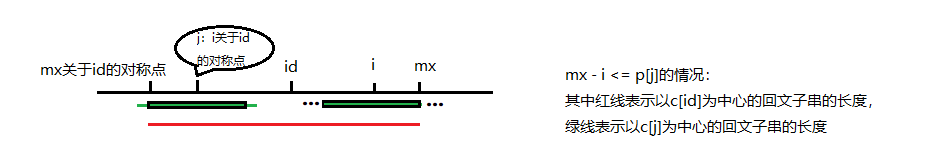
如果mx <= i ，则说明字符c[i]不在以c[id]为中心的回文子串中，那么此时以c[i]为中心的回文子串半径至少是1。

如何求c[i]的对称字符c[j]：字符c[id]到c[j]的距离id-j等于字符c[i]到字符c[id]的距离i-id，即id-j=i-id，那么就可以得出j=2*id-i【j为字符c[j]的下标】

时间复杂度分析：

for 循环里边套了一层 while 循环，难道不是 O(n²)？不！其实是 O(n)。不严谨的想一下，因为 while 循环访问 R 右边的数字用来扩展，也就是那些还未求出的节点，然后不断扩展，而期间访问的节点下次就不会再进入 while 了，可以利用对称得到自己的解，所以每个节点访问都是常数次，所以是 O ( n )。【由于Manacher算法只有遇到没有匹配过的位置才进行匹配，对于匹配过的位置不再重复匹配，所以对于字符串中的每个字符只进行一次匹配，所以时间复杂度为O(n)。】

 //Manacher算法，时间复杂度O(n)
    private static String longestPalindrome(String s) {
        StringBuilder sb = new StringBuilder("$#"); //先添加"$#"字符串
        for (int i = 0; i < s.length(); i++) {
            sb.append(s.charAt(i)).append("#"); //在s的每一个字符后都添加#字符
        }
        String ns = sb.toString();
        int id = 0; //用来记录目前已经求得的以每个字符为中心，能延伸到目前来说最往右的回文子串的中心
        int mx = 0; //用来记录以id为中心p[id]为半径的那个回文子串的最右边字符所在的位置（下标）
        int resLen = 0; //用来记录最长回文子串的长度
        int resCenter = 0; //用来记录最长回文子串的中心
        char[] c = ns.toCharArray();
        int[] p = new int[c.length];
        for (int i = 1; i < c.length; i++) {
            p[i] = (mx > i) ? Math.min(p[2 * id - i], mx - i) : 1;
            while (i + p[i] < c.length && c[i + p[i]] == c[i - p[i]]) {//注意此时一定要防止i+p[i]越界
            //以level为例，$#l#e#v#e#l#   算到第二个l时，此时p[10]=2  i+p[i]=10+2=12==12 下标越界
                //以levele为例，$#l#e#v#e#l#e#  算到第二个l时，此时p[10]=2 i+p[i]=10+2<14  继续匹配
                p[i]++;
            }
            if (mx < i + p[i]) {
                mx = i + p[i];
                id = i;
            }
            if (resLen < p[i]) {
                resLen = p[i];
                resCenter = i;
            }
        }
        int start = (resCenter - resLen) / 2; //最长回文子串的起始位置、起始下标
        return s.substring(start, start + resLen - 1);
    }