GDKOI 2012--mmm含树

这是今年GDKOI的一题：有一棵树，开始时所有结点的值都是0。有多个操作，每个操作有两种：

1.对某个点增加w，设dis（i，j）为点i到点j的最短距离，那么某个结点增加w时，对于任意一个结点j，它的值会增加w + dis（i，j）。

2.询问某点的值。

w可以忽略，因为整棵树都要加上w，只要记下所有w的和就可以了，输出答案时再加上。这题的突破口就是只需要求一个点的值，这就取决于其他发生变化的点对该点的影响。这里先结合一个样例，说明一些变量：

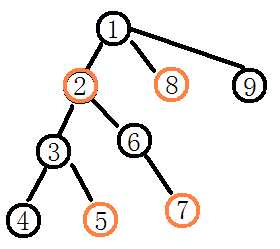
如图：点2，5，7，8被修改过（忽略了w）。

dis（i，j）：点i到点j的最短距离。

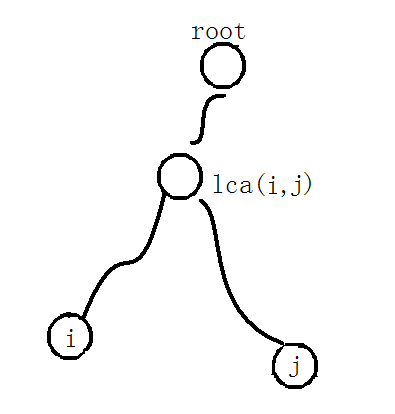
lca（i，j）：点i和点j的最近公共祖先。

dep（i）：点i到根结点的距离，dep（6）= 2，dep（5）= 3。

cnt（i）：以i为根的子树中的点，被修改过的次数，cnt（3）= 1，cnt（2）= 3。

deps（i）：以i为根的子树中的被修改过的点的dep和，deps（2） = dep（2）+ dep（5）+ dep（7） = 1 + 3 + 3 = 7。

首先，要求任意两点i，j的距离，用dis（i，j）来表示是不好的，因为这没有内在的关系。这个可以表示成dep（i）+ dep（j）- 2 * dep（lca（i，j））。画个图就知道了。

如样例，有一个询问，询问3的值，那么它等于：

dep（3）* cnt（3） + deps（3） - 2 * dep（3）* cnt（3）

+dep（3）* （cnt（2）- cnt（3）） + （deps（2）- deps（3）） - 2 * dep（2）*（cnt（2）- cnt（3））

+dep（3）* （cnt（1）- cnt（2）） + （deps（1）- deps（2）） - 2 * dep（1）*（cnt（1）- cnt（2））

可以发现，有很多值是可以约去的，还有dep（2）= dep（3）- 1，dep（1）= dep（3）- 2，化简得：

dep（3） * cnt（1） +  deps（1） - 2 * （cnt（3） + cnt（2））。

再可以由此推到普遍：

询问点u：dep（u） * cnt（1） +  deps（1） - 2 * （cnt（u） + cnt（u的父亲） + cnt（u的父亲的父亲） + … + cnt（根的儿子））。注意不要加到根。

如此看来，我们需要的只是求cnt的和。这个可以用树链剖分来统计。

对于这些改一些，问一些的题目，不要局限于维护答案的值，可以通过维护其他的信息，以便于求答案。