在一百年前,行列式不是线性代数的中心,但是数学的方向一直在变换!毕竟,仅仅一个数就能告诉我们许多矩阵的信息。
对行列式的一种理解是:它对
A−1,A−1b
的每一项给出了明确的方式,这个公式不会随着我们的计算方法而改变。事实上,我们可以将行列式看成
n×n
矩阵最有效的替代公式,这个公式说明了
A−1
如何依赖
A
的
现在我们列出行列式的四个主要用途:
他们可以判断可逆性。如果 A 的行列式为零,那么
A 是奇异的;如果 detA≠0 ,那么 A 是可逆的(A−1 涉及到 1/detA )。最重要的应用是矩阵 A−λI ,主对角线上的元素减去参数 λ ,问题是找出奇异值,此时 A−λI 是奇异的,这时候就需要检查 det(A−λI)=0 ,这个关于 λ 的 n 阶多项式有
n 个解,矩阵有 n 个特征值,这个事实来自于行列式的公式,而不是计算出来的。A 的行列式等于 n 维空间里盒子的体积。盒子的边是A 的行(图1), A 的列给出完全不同的盒子,但是体积是相等的。最简单的盒子是一个小立方体
dV=dxdydz ,就像 ∫∫∫f(x,y,z)dV ,假设我们用柱坐标表示,那么 x=rcosθ,y=rsinθ,z=z ,正如一个很小的区间 dx 被拉伸成 (dx/du)du ,所以体积元变成 Jdrdθdz ,雅克比行列式是类似 dx/du ,只不过是扩展到三维空间:
这个行列式的值为 J=r 。行列式对每个主元给出了一个公式。理论上,我们可以推断主元是否为零,当然可能需要进行行交换。而根据公式:行列式= ± (主元的乘积),不管是否进行交换,主元乘积的绝对值是一样的。
许多年前,因为这个结论使得大家认为通过行交换来避免较小的主元是没有任何用的,因为最终还是有小的主元。但是在实践中,如果异常小的主元不可避免时,通过也会有一个异常大的主元,这样的话乘积的结果会带回到正常情况。
行列式度量 A−1b 对 b 上每个元素的依赖性。如果实验中的一个参数改变了,或者一个观测量是正确的,那么
A−1 的影响系数就是行列式的一个比值。关于行列式还有一个问题,不仅仅确定它的重要性以及在线性代数中的位置很困难,而且给出最好的定义也很困难。很明显, detA 不是 n2 个变量的某个简单函数;另外 A−1 比行列式更容易求出。
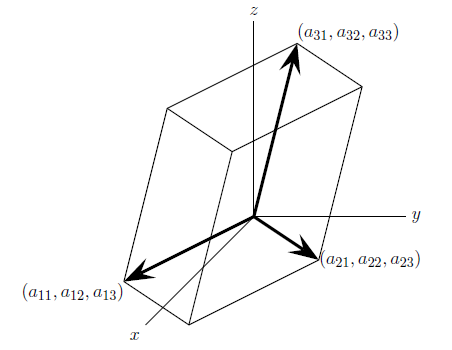
图1
对于行列式而言,最简单的不是明确的表达式,而是它的属性。它可以用三个最基本的属性定义: detI=1 ,执行一次行交换符号的反转一次,行列式和每行是线性关系。那么现在的问题就是利用这三个属性系统的说明怎么计算行列式。
(PS:这里给出接下来几篇文章的具体安排)下一篇文章会解释行列式的这三条性质以及他们最重要的结论;然后我们会给出行列式的公式——一个有 n! 项的大公式以及一个归纳公式;再然后我们应用行列式来求解 A−1 ,由此我们用克莱姆法则计算 x=A−1b ;最后,讨论一下置换,不管我们以怎样的顺序使用这些性质,结果都是一样的——也就是说这些性质是自洽的。
这里留一个简单的关于置换的问题,将VISA变成AVIS需要多少次变换?这个变换是奇数次还是偶数次?








 本文探讨了行列式在线性代数中的核心地位及其四大应用:判断矩阵的可逆性、寻找特征值、计算几何体积及衡量逆矩阵的依赖性。文章还将介绍行列式的性质、计算方法,并使用克莱姆法则解决线性方程组。
本文探讨了行列式在线性代数中的核心地位及其四大应用:判断矩阵的可逆性、寻找特征值、计算几何体积及衡量逆矩阵的依赖性。文章还将介绍行列式的性质、计算方法,并使用克莱姆法则解决线性方程组。
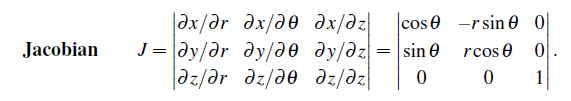

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








