矩阵乘法问题
设矩阵A,B是nxn的方阵,我们将用分治法求解 C=A*B 。
我们用蛮力方法求解的运行时间复杂度为:。利用分治法,将A,B,C划分成4个n/2 x n/2 的矩阵,如下:
所以有:
采用分治思想,其伪代码表示如下:
其时间复杂度为:
为减小时间复杂度,采用Strassen 法,其原理仍将讲矩阵A,B,C划分成n/2 x n/2 ,然后按如下计算:
其时间复杂度为:
两种分治方法的完整代码如下:
#include<iostream>
#include<fstream>
#include<cmath>
#include<string>
#include<ctime>
#include<cstdlib>
#include<iomanip>
using namespace std;
void Print(int **M,int n)
{//Print the Matrix
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
cout<<setw(5)<<M[i][j];
cout<<endl;
}
}
int **AllocSize(int n)
{//malloc size for Matrix
int **M;
M=new int*[n];
for(int i=0;i<n;i++)
M[i]=new int[n];
return M;
}
int **getMatrix(int n)
{//Randomly generate Matrix
int **M;
//srand((unsigned)time(NULL)); //generate the same random number
M=AllocSize(n);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
M[i][j]=rand()%9+1;
return M;
}
void Matrix_Divide(int **A,int **A11,int **A12,int **A21,int **A22,int n)
{//Divide Matrix A into A11,A12,A21,A22
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
A11[i][j]=A[i][j];
A12[i][j]=A[i][j+n];
A21[i][j]=A[i+n][j];
A22[i][j]=A[i+n][j+n];
}
}
int **Matrix_Sub(int **A,int **B,int n)
{//Matrix Sub
int **C;
C=AllocSize(n);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
C[i][j]=A[i][j]-B[i][j];
return C;
}
int **Matrix_Add(int **A,int **B,int n)
{//Matrix Add
int **C;
C=AllocSize(n);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
C[i][j]=A[i][j]+B[i][j];
return C;
}
void Matrix_Unit(int **C,int **C11,int **C12,int **C21,int **C22,int n)
{//Unit Matrix C11,C12,C21,C22 into Matrix C
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
C[i][j] =C11[i][j];
C[i][j+n] =C12[i][j];
C[i+n][j] =C21[i][j];
C[i+n][j+n]=C22[i][j];
}
}
int **DC_MatrixMul(int **A,int **B,int n)
{//Matrix Multiplication using Divide-and-Conquer
int **C;
C=AllocSize(n);
if(n==1)
C[0][0]=A[0][0]*B[0][0];
else
{
n=n/2;
int **A11,**A12,**A21,**A22;
int **B11,**B12,**B21,**B22;
int **C11,**C12,**C21,**C22;
int **T1,**T2;
A11=AllocSize(n);
A12=AllocSize(n);
A21=AllocSize(n);
A22=AllocSize(n);
B11=AllocSize(n);
B12=AllocSize(n);
B21=AllocSize(n);
B22=AllocSize(n);
C11=AllocSize(n);
C12=AllocSize(n);
C21=AllocSize(n);
C22=AllocSize(n);
T1=AllocSize(n); //temporary Matrix T1,T2
T2=AllocSize(n);
Matrix_Divide(A,A11,A12,A21,A22,n);
Matrix_Divide(B,B11,B12,B21,B22,n);
T1=DC_MatrixMul(A11,B11,n);
T2=DC_MatrixMul(A12,B21,n);
C11=Matrix_Add(T1,T2,n);
T1=DC_MatrixMul(A11,B12,n);
T2=DC_MatrixMul(A12,B22,n);
C12=Matrix_Add(T1,T2,n);
T1=DC_MatrixMul(A21,B11,n);
T2=DC_MatrixMul(A22,B21,n);
C21=Matrix_Add(T1,T2,n);
T1=DC_MatrixMul(A21,B12,n);
T2=DC_MatrixMul(A22,B22,n);
C22=Matrix_Add(T1,T2,n);
Matrix_Unit(C,C11,C12,C21,C22,n);
}
return C;
}
int **Strassen_MatrixMul(int **A,int **B,int n)
{
int **C;
C=AllocSize(n);
if(n==1)
C[0][0]=A[0][0]*B[0][0];
else
{
n=n/2;
int **A11,**A12,**A21,**A22;
int **B11,**B12,**B21,**B22;
int **C11,**C12,**C21,**C22;
int **S1,**S2,**S3,**S4,**S5,**S6,**S7,**S8,**S9,**S10;
int **P1,**P2,**P3,**P4,**P5,**P6,**P7;
int **T1,**T2;
A11=AllocSize(n);
A12=AllocSize(n);
A21=AllocSize(n);
A22=AllocSize(n);
B11=AllocSize(n);
B12=AllocSize(n);
B21=AllocSize(n);
B22=AllocSize(n);
C11=AllocSize(n);
C12=AllocSize(n);
C21=AllocSize(n);
C22=AllocSize(n);
S1 =AllocSize(n);
S2 =AllocSize(n);
S3 =AllocSize(n);
S4 =AllocSize(n);
S5 =AllocSize(n);
S6 =AllocSize(n);
S7 =AllocSize(n);
S8 =AllocSize(n);
S9 =AllocSize(n);
S10=AllocSize(n);
P1 =AllocSize(n);
P2 =AllocSize(n);
P3 =AllocSize(n);
P4 =AllocSize(n);
P5 =AllocSize(n);
P6 =AllocSize(n);
P7 =AllocSize(n);
T1=AllocSize(n);
T2=AllocSize(n);
Matrix_Divide(A,A11,A12,A21,A22,n);
Matrix_Divide(B,B11,B12,B21,B22,n);
S1 =Matrix_Sub(B12,B22,n);
S2 =Matrix_Add(A11,A12,n);
S3 =Matrix_Add(A21,A22,n);
S4 =Matrix_Sub(B21,B11,n);
S5 =Matrix_Add(A11,A22,n);
S6 =Matrix_Add(B11,B22,n);
S7 =Matrix_Sub(A12,A22,n);
S8 =Matrix_Add(B21,B22,n);
S9 =Matrix_Sub(A11,A21,n);
S10=Matrix_Add(B11,B12,n);
P1=Strassen_MatrixMul(A11,S1,n);
P2=Strassen_MatrixMul(S2,B22,n);
P3=Strassen_MatrixMul(S3,B11,n);
P4=Strassen_MatrixMul(A22,S4,n);
P5=Strassen_MatrixMul(S5, S6,n);
P6=Strassen_MatrixMul(S7, S8,n);
P7=Strassen_MatrixMul(S9,S10,n);
T1 =Matrix_Add(P5,P4,n);
T2 =Matrix_Sub(P2,P6,n);
C11=Matrix_Sub(T1,T2,n);
C12=Matrix_Add(P1,P2,n);
C21=Matrix_Add(P3,P4,n);
T1 =Matrix_Add(P5,P1,n);
T2 =Matrix_Add(P3,P7,n);
C22=Matrix_Sub(T1,T2,n);
Matrix_Unit(C,C11,C12,C21,C22,n);
}
return C;
}
int main()
{
int n=4;
int **A,**B,**C;
cout<<"The maxtrix A is:"<<endl;
A=getMatrix(n);
Print(A,n);
cout<<"The matrix B is:"<<endl;
B=getMatrix(n);
Print(B,n);
cout<<"The DC_mul result C is:"<<endl;
C=DC_MatrixMul(A,B,n);
Print(C,n);
cout<<"The Strassen_mul result C is:"<<endl;
C=Strassen_MatrixMul(A,B,n);
Print(C,n);
return 0;
}
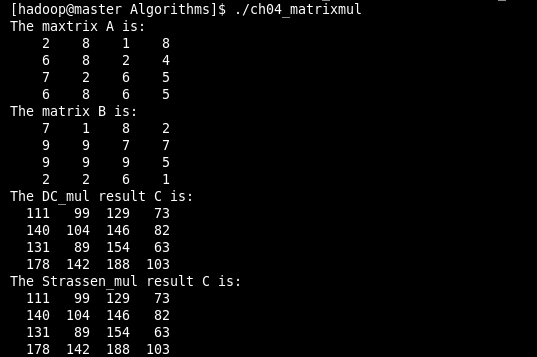
运行结果如下:
、








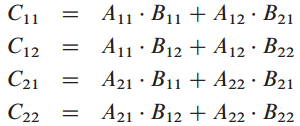

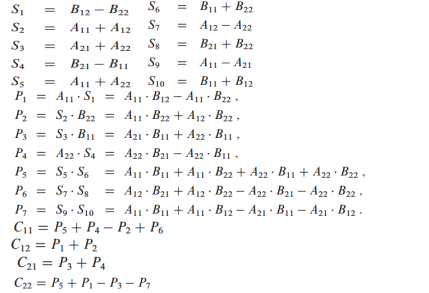














 717
717

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








