在一个由n个元素组成的集合中,第i个顺序统计量(order statistic)即为该集合中第i小的元素。当i=1时,即为最小值;当i=n时,即为最大值;当i=L(n+1)/2」时,即为中位数(median)。求第i个顺序统计量可以定义为形式化的定义为选择问题(selection problem):
输入:一个包含n个(不同的)的书的集合A和一个数i,1≤i≤n
输出:元素x∈A,它恰大于A中其他的i-1个元素
该问题可以通过排序在O(nlgn)时间内解决,但是该问题可以在线性时间内求解。
方法一(以期望线性时间做选择):
类似快速排序的思想,随机选择主元对输入数组进行递归划分。然后对划分的一边进行处理即可(快速排序需要处理两边)。伪代码如下:
性能分析:
假设E(T(n)) ≤ cn ,然后用数学归纳法证之。
方法二(最坏情况线性时间的选择):
由于方法一随机选取主元并不能保证每次是最好的选择,但可以通过对输入数组的递归划分来保证每次对数组的划分是一个好的划分。步骤如下:
1)将输入数组的n个元素划分为Ln/5」,每组5个元素,且至多只有一组由剩下的n mod 5 个元素组成
2)寻找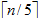
3)对第2步中找出的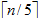
4)利用修改过的PARTITION过程,按中位数的中位数x对输入的数组进行划分,让k比划分低区的元素数目多1,所以x是第k小的元素,并且有n-k个元素在划分的高区
5)如果i=k,则返回x;否则,如果i<k,则在低区递归调用SELECT以找出第i小的元素;如果i>k,则在高区中找第(i-k)个最小元素。
性能分析:
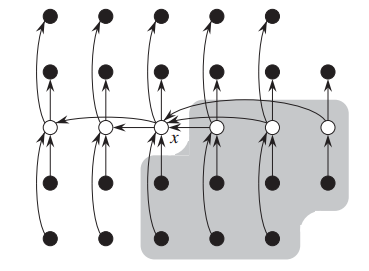
如图,阴影区域表示大于x的元素
大于(或小于)x的元素个数至少为:
在最后情况下,第5步中最多有7n/10+6个元素递归调用SELECT。
对于整个算法,可以得到递归式:
解得,
T(n)=O(n)
两种方法完整代码如下:
#include<iostream>
#include<cstdlib>
#include<ctime>
#include<climits>
#include<iomanip>
#define N 5
using namespace std;
void Print(int *A)
{
int n=A[0];
for(int i=1;i<=n;i++)
{
cout<<setw(5)<<A[i];
if(i%10==0)
cout<<endl;
}
cout<<endl;
}
void getTestData(int *A,int n)
{//generate random test data
srand((unsigned)time(NULL));
for(int i=1;i<=n;i++)
A[i]=rand()%100;
A[0]=n;
}
int *cpArr(int *a)
{
int n=a[0];
int *b=new int[n+1];
for(int i=1;i<=n;i++)
b[i]=a[i];
b[0]=n;
return b;
}
/*-----------------------Randomized select in expected linear time----------------------*/
void swap(int &a,int &b)
{
int temp;
temp=a;
a=b;
b=temp;
}
int Partition(int *A,int p,int r)
{
int x=A[r];
int i=p-1;
for(int j=p;j<=r-1;j++)
if(A[j]<x)
{
i=i+1;
swap(A[i],A[j]);
}
swap(A[i+1],A[r]);
return i+1;
}
int Randomized_Partition(int *A,int p,int r)
{
srand((unsigned)time(NULL));
int i=rand()%(r-p+1)+p;
swap(A[i],A[r]);
return Partition(A,p,r);
}
int Randomized_Select(int *A,int p,int r,int i)
{//return ith smallest number
if(p==r)
return A[p];
int q=Randomized_Partition(A,p,r);
int k=q-p+1;
if(i==k) //the pivot value is the answer
return A[q];
else if(i<k)
return Randomized_Select(A,p,q-1,i);
else
return Randomized_Select(A,q+1,r,i-k);
}
/*-----------------------------------------------------------------------------*/
/*--------------------Selection in worst-case linear time----------------------*/
int Select(int *A,int p,int r,int i);
int getMidByInsertSort(int *A,int begin,int end)
{//insert sort,return the meadian of one group
int glen=end-begin+1; //the length of each group
int gmid=(glen+1)/2;
for(int i=begin+1;i<=end;i++)
for(int j=i-1;j>=begin && A[j]>A[j+1]; j--)
swap(A[j],A[j+1]);
return A[gmid];
}
int getMid(int *A,int p,int r)
{//get the median of medians value
int length=r-p+1;
int groups;
int begin , end;
if(length % N==0) //each group contain N elements
groups=length/N;
else
groups=length/N+1;
int *mediansArr=new int[groups+1];
for(int i=1;i<=groups ;i++)
{
int begin=p+(i-1)*N; // the beginning position of each group
if(length%N!=0 && i==groups)//when the last groups isn't N,the end position is r
end=r;
else
end=p+i*N-1;
mediansArr[i]=getMidByInsertSort(A,begin,end); //medians of each group
}
return Select(mediansArr,1,groups,(groups+1)/2); //find medians in medianArr,wich stores medians of each group
}
int PartitionByMid(int *A,int p,int r,int mid)
{//exchange A[mid] with A[r]
for(int j=p;j<r;j++)
if(A[j]==A[mid])
{
swap(A[mid],A[r]);
break;
}
return Partition(A,p,r);
}
int Select(int *A,int p,int r,int i)
{
if(p==r)
return A[p];
int mid=getMid(A,p,r); //mid is the median-of-medians
int q=PartitionByMid(A,p,r,mid); //split array A to A[p..q-1]<=mid<A[q+1..r]
int k=q-p+1;
if(i==k)
return A[q];
else if(i<k)
return Select(A,p,q-1,i);
else
return Select(A,q+1,r,i-k);
}
/*-----------------------------------------------------------------------------*/
int main()
{
int n=12;
int *A,*A1;
int i=4;
cout<<"-------------Randomized-select version-----------------"<<endl;
cout<<"Input the total number n:";
cin>>n;
cout<<"Input the ith smallest's i:";
cin>>i;
A=new int[n+1];
cout<<"The random test data:"<<endl;
getTestData(A,n);
Print(A);
A1=cpArr(A); //copy array A.
int iSmallest1=Randomized_Select(A,1,n,i);
cout<<"The "<<i<<"th smallest is:"<<iSmallest1<<endl;
cout<<"--------Select in worst-case linear time-------------"<<endl;
Print(A1);
int iSmallest2=Select(A1,1,n,i);
cout<<"The "<<i<<"th smallest is:"<<iSmallest2<<endl;
return 0;
}
【注:若有错误,请指正~~~】





 本文介绍了两种线性时间复杂度的选择算法,一种是期望线性时间的选择算法,另一种是最坏情况线性时间的选择算法。这两种算法都可用于找到未排序数组中的第i小的元素,即第i个顺序统计量。
本文介绍了两种线性时间复杂度的选择算法,一种是期望线性时间的选择算法,另一种是最坏情况线性时间的选择算法。这两种算法都可用于找到未排序数组中的第i小的元素,即第i个顺序统计量。


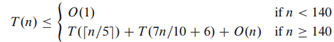
















 1372
1372

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








