算法基础-顺序统计量

前往我的主页以获得更好的阅读体验算法基础-顺序统计量 - DearXuan的主页https://blog.dearxuan.com/2022/01/30/%E7%AE%97%E6%B3%95%E5%9F%BA%E7%A1%80-%E9%A1%BA%E5%BA%8F%E7%BB%9F%E8%AE%A1%E9%87%8F/

顺序统计量

将长度为 n 的数组升序排序后，则第 i 个位置的数字是该数组的第 i 小的量，称之为第 i 顺序统计量

数组最小值是第1个顺序统计量，最大值是第n个顺序统计量，中位数(又称下中位数)是第⌊(n+1)/2⌋个顺序统计量

⌊n⌋ 表示对 n 向下取整，⌈n⌉表示对 n 向上取整

最大值和最小值

若想要寻找n个数字里的最大值或最小值，只需要进行(n-1)次比较

int min = a[0];
for(int i=1;i<n;i++){
    if(a[i] > min)
        min = a[i];
}

显然这已经是最优的算法了，我们称他为“遍历查找”，因为该算法是简单地遍历了整个数组来寻找最大或最小值，总共需要(n-1)次比较，即S(n)=n-1

现在我们要研究如何以尽可能低的时间复杂度来同时求出数组的最大值和最小值

传统方法

最容易想到的方法就是重复两次“遍历查找”，分别找出最大和最小值，那么就需要S(n)=2(n-1)次比较，但是这显然不是最佳的方案。

设存在数组A=[9,0,1,2,100]

在寻找最小值时，当遍历到第2个元素时，由于0<9，所以最小值被替换成0，同时我们也可以得知0一定不是最大值，因为有个9比它更大。

在寻找最大值时，采用了相同的算法，导致0又被比较了一遍，而现在0不可能是最大值。

优化算法

通过上面的传统方法，我们可以发现减少比较次数的关键是减少不必要的比较，这就给我们一个思路，将一个数组划分为 k 段，找出这 k 个数的最大最小值，然后分别和整个数组的最大最小值比较

设查找长度为 n 的数组中的最大最小值，需要比较至多 f(n) 次，数组被划分为 n/k 段，每段 k 个数字，每段分别需要比较 f(k) 次就可以得到最大最小值，则共比较就可以得到 n/k 个最大值数组和最小值数组，在查找整个数组的最小值时只需要从最小值数组里寻找就行了，而查找整个数组的最大最小值又需要比较次，于是得到 f(n) 的函数

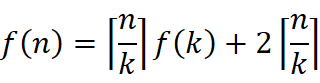
同理对于长度为k的数组，我们又可以将其分为更小的段，一直分下去，直到 k = 2 时，f(2)=1，因为两个数只需要比较一次就能得到最大最小值，我们假设将长度为n的数组划分为长度为k1的数段，将长度为k(i-1)的数段划分为长度为ki的更小的数段，带入 f(n)，得

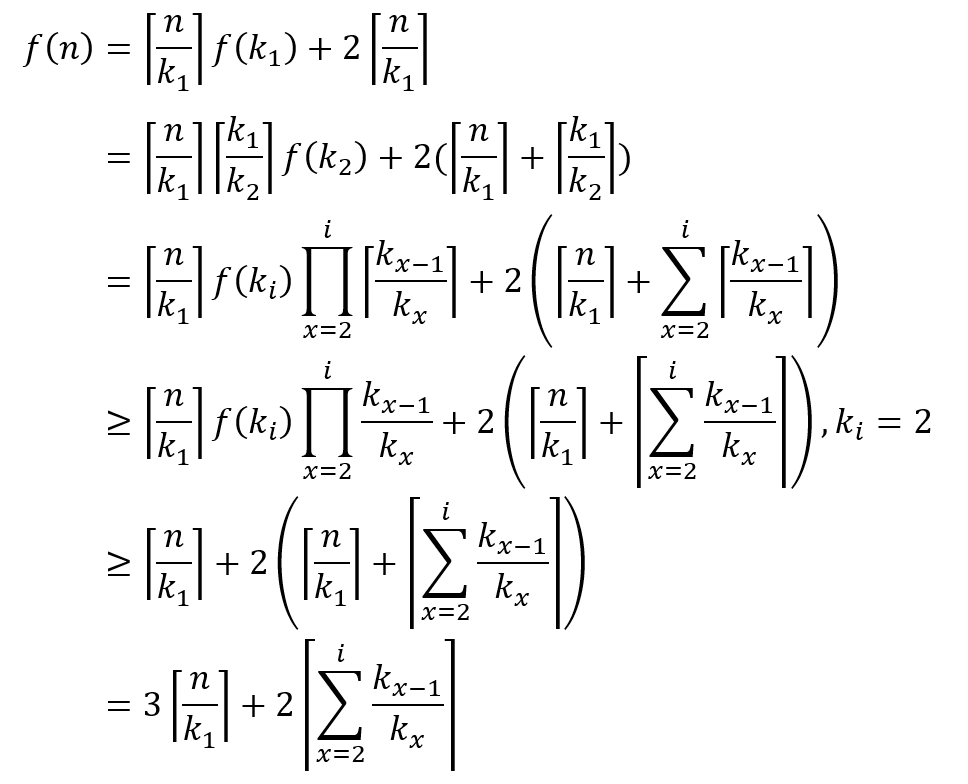
 由于 kx 一定是正数，因此 i 为 1 时，右边的连加消失，f(n)取到最小值，即k1=2

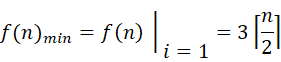
得到上述结果的前提是事先定义好了min和max的初值，但是实际应用中我们可以根据数组动态调整初值，如果长度为偶数，则先比较前两项，大的作为max，小的作为min，共比较(3n/2-1)次；如果长度为奇数，则min和max都取第一项，因此实际的比较次数应该是(3n/2-2)次，即最终比较次数应该是

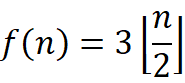
 通过理论我们得知了只要把数组中的数两两比较，其中的较小者和最小值比较，而较大者和最大值比较，就可以实现用最少的比较次数同时求出最大最小值

void FindMinAndMax(int* a, int len){
    int min, max, i;
    if(len % 2 == 0){
        //当长度为偶数时，将前两项之间的较大者设为最大值，较小者设为最小值
        if(a[0] < a[1]){
            min = a[0];
            max = a[1];
        }else{
            min = a[1];
            max = a[0];
        }
        //从a[2]和a[3]开始比较，i为3
        i = 3;
    }else{
        //当长度为基数时，将最大值和最小值都设为a[0]
        min = max = a[0];
        //从a[1]和a[2]开始比较，i为2
        i = 2;
    }
    while (i < len){
        if(a[i-1] < a[i]){
            if(a[i-1]<min) min = a[i-1];
            if(a[i]>max) max = a[i];
        }else{
            if(a[i]<min) min = a[i];
            if(a[i-1]>max) max = a[i-1];
        }
        i += 2;
    }
    cout << "min:" << min << endl;
    cout << "max:" << max << endl;
}

第i顺序统计量

如果想要找到数组里的第 i 顺序统计量，也就是第 i 小的数字，通常的办法是把整个数组排序，然后直接取出对应位置的数字。快速排序是一个很好的办法，快速排序将数组划分为两个子数组来排序。实际上，我们只关心其中某一个位置的数字，因此对于快速排序划分出来的两个子数组，我们仅需要排序其中一个就行了

int find(int *a, int left, int right, int k) {
    if (left >= right) {
        return a[left];
    }
    //key为选定的基准值
    int i = left, j = right, key = a[left];
    while (i < j) {
        //遍历数组找到第一个比key大的数
        while (a[i] < key) {
            ++i;
        }
        //遍历数组找到第一个比key小的数
        while (a[j] > key) {
            --j;
        }
        //交换，此时比key小的在左边，比key大的在右边
        if (i < j) {
            int temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    }
    //此时基准值在整个数组的第i个位置
    //s是基准值在以left开始的数组里的位置，i是基准值的位置
    int s = i - left + 1;
    if (s == k) {//如果s==k,说明基准值就是要查找的数,则返回基准值
        return a[i];
    } else if (s > k) {//如果s>k,说明基准值在要查找的数的右边,则遍历左边数组
        return find(a, left, j, k);
    } else {//如果s<k,说明基准值在要查找的数的左边,则遍历右边数组
        return find(a, j + 1, right, k - s);
    }
}

该方法的比较次数受到随机因素的影响，因此是一个随机算法。在平均情况下，它的时间复杂度能够达到O(n)