Graham扫描法求点集凸包的原理及代码实现

Graham扫描法

时间复杂度：O(n㏒n) 
思路：Graham扫描的思想和Jarris步进法类似，也是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，但它不是利用夹角。 
 
步骤：

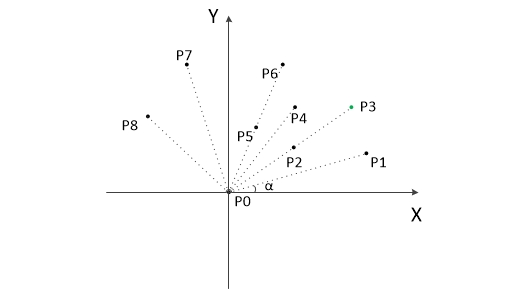
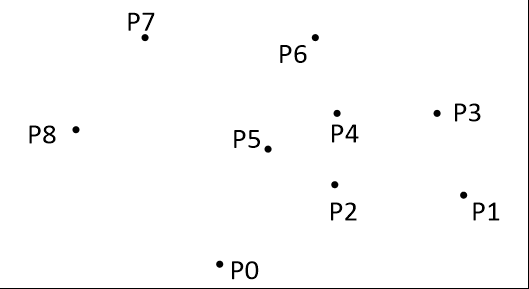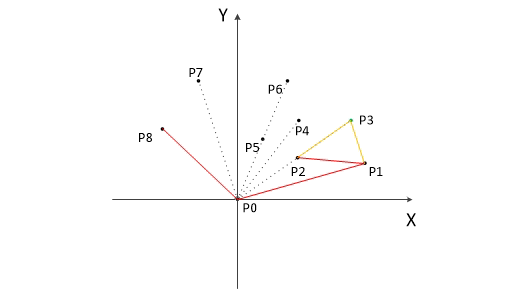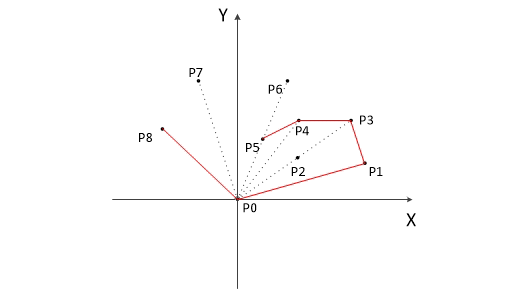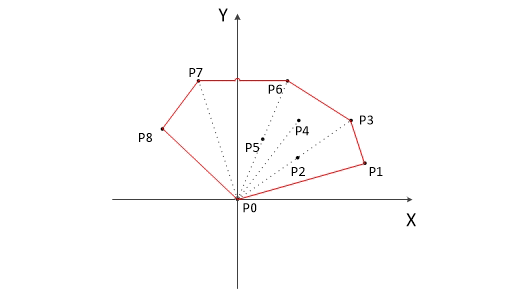
1. 把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。
2. 把所有点的坐标平移一下，使 P0 作为原点，如上图。
3. 计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。 
   （以上是准备步骤，以下开始求凸包） 
   以上，我们已经知道了凸包上的第一个点 P0 和第二个点 P1，我们把它们放在栈里面。现在从步骤3求得的那个结果里，把 P1 后面的那个点拿出来做当前点，即 P2 。接下来开始找第三个点：
4. 连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。
5. 如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。
6. 当前点是凸包上的点，把它压入栈，执行步骤7。
7. 检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。

最后，栈中的元素就是凸包上的点了。 
以下为用Graham扫描法动态求解的过程： 

                             

                                  

                            

                                 

                        

                                                         

 下面给出求一堆点的凸包的点集的代码                        

typedef struct{
    double x,y;
}POINT;

POINT result[101];//模拟堆栈s，保存凸包上的点
POINT tree[101];
int n,top;

double Distance(POINT p1,POINT p2){
    return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}

double Multiply(POINT p1,POINT p2,POINT p3){
    return (p2.x-p1.x)*(p3.y-p1.y)-(p3.x-p1.x)*(p2.y-p1.y);
}

int cmp(const void *p1,const void *p2){
    POINT *p3,*p4;
    double m;
    p3 = (POINT *)p1;
    p4 = (POINT *)p2;
    m = Multiply(tree[0],*p3,*p4);
    if(m < 0)return 1;
    else if(m == 0&&Distance(tree[0],*p3)<Distance(tree[0],*p4)){
        return 1;
    }else
        return -1;
}

void Tubao(){
    int i;
    int pos;
    double temp,px,py;
    while(~scanf("%d",&n)){//n是输入点的个数
        py = -1;
        for(i = 0;i < n;i++){
            scanf("%lf%lf",&tree[i].x,&tree[i].y);
        }
        for(i = 0;i < n;i++){
            if(py == -1 || tree[i].y < py){
                py = tree[i].y;
                px = tree[i].x;
                pos = i;
            }else if(tree[i].y == py&&tree[i].x < px){
                py = tree[i].y;
                px = tree[i].x;
                pos = i;
            }
        }
        temp = tree[0].x;
        tree[0].x = tree[pos].x;
        tree[pos].x = temp;
        temp = tree[0].y;
        tree[0].y = tree[pos].y;
        tree[pos].y = temp;
        qsort(&tree[1],n-1,sizeof(double)*2,cmp);
        tree[n].x = tree[0].x;
        tree[n].y = tree[0].y;
        result[0].x = tree[0].x;
        result[0].y = tree[0].y;
        result[1].x = tree[1].x;
        result[1].y = tree[1].y;
        result[2].x = tree[2].x;
        result[2].y = tree[2].y;
        top = 2;
        for(i = 3;i <= n;i++){
            while(Multiply(result[top-1],result[top],tree[i]) <= 0){
                top--;
            }
            result[top+1].x = tree[i].x;
            result[top+1].y = tree[i].y;
            top++;
        }
    }