一、范数
被选择的参数,应该使算出的函数曲线与观测值之差的平方和最小。用函数表示为:
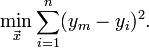
用欧几里得度量表达为:

1-范数:是指向量(矩阵)里面非零元素的个数。类似于求棋盘上两个点间的沿方
格边缘的距离。||x||1 = sum(abs(xi));
2-范数(或Euclid范数):是指空间上两个向量矩阵的直线距离。类似于求棋盘上两点见的直线距离 (无需只沿方格边缘)。
||x||2 = sqrt(sum(xi.^2));
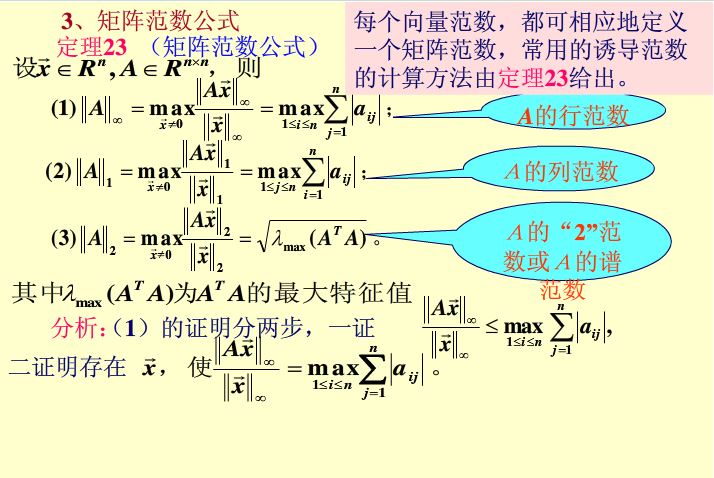
∞-范数(或最大值范数):顾名思义,求出向量矩阵中其中模最大的向量。
||x||∞ = max(abs(xi));

二、简单线性回归
被选择的参数,应该使算出的函数曲线与观测值之差的平方和最小。用函数表示为:
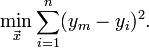
用欧几里得度量表达为:

线性函数模型。最简单的线性式是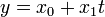 ,写成行列式,为
,写成行列式,为
直接给出该式的参数解:
-
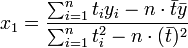 和
和 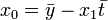
其中 ,为t值的算术平均值。也可解得如下形式:
,为t值的算术平均值。也可解得如下形式:
简单线性模型 y = x0 + x1t 的例子
随机选定10艘战舰,并分析它们的长度与宽度,寻找它们长度与宽度之间的关系。由下面的描点图可以直观地看出,一艘战舰的长度(t)与宽度(y)基本呈线性关系。散点图如下: 
以下图表列出了各战舰的数据,随后步骤是采用最小二乘法确定两变量间的线性关系。
| 编号 | 长度 (m) | 宽度 (m) | ti - t | yi - y | |||
|---|---|---|---|---|---|---|---|
| i | ti | yi | ti* | yi* | ti*yi* | ti*ti* | yi*yi* |
| 1 | 208 | 21.6 | 40.2 | 3.19 | 128.238 | 1616.04 | 10.1761 |
| 2 | 152 | 15.5 | -15.8 | -2.91 | 45.978 | 249.64 | 8.4681 |
| 3 | 113 | 10.4 | -54.8 | -8.01 | 438.948 | 3003.04 | 64.1601 |
| 4 | 227 | 31.0 | 59.2 | 12.59 | 745.328 | 3504.64 | 158.5081 |
| 5 | 137 | 13.0 | -30.8 | -5.41 | 166.628 | 948.64 | 29.2681 |
| 6 | 238 | 32.4 | 70.2 | 13.99 | 982.098 | 4928.04 | 195.7201 |
| 7 | 178 | 19.0 | 10.2 | 0.59 | 6.018 | 104.04 | 0.3481 |
| 8 | 104 | 10.4 | -63.8 | -8.01 | 511.038 | 4070.44 | 64.1601 |
| 9 | 191 | 19.0 | 23.2 | 0.59 | 13.688 | 538.24 | 0.3481 |
| 10 | 130 | 11.8 | -37.8 | -6.61 | 249.858 | 1428.84 | 43.6921 |
| 总和(Σ) | 1678 | 184.1 | 0.0 | 0.00 | 3287.820 | 20391.60 | 574.8490 |
仿照上面给出的例子
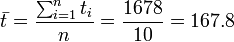 并得到相应的
并得到相应的 .
.
然后确定x1
可以看出,战舰的长度每变化1m,相对应的宽度便要变化16cm。并由下式得到常数项x0:
-

-
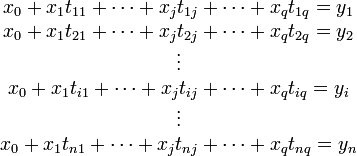
-
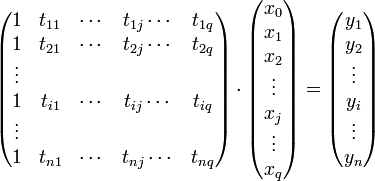 即
即 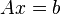
-
 。
。
-
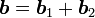
-

-

-
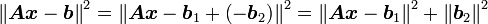
-

-
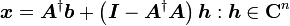
-
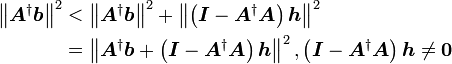
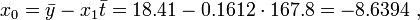
三、一般线性情况
含有更多不相关模型变量 ,可如组成线性函数的形式
,可如组成线性函数的形式
即线性方程组
通常人们将tij记作数据矩阵 A,参数xj记做参数矢量x,观测值yi记作b,则线性方程组又可写成:
上述方程运用最小二乘法导出为线性平差计算的形式为:
最小二乘法的解
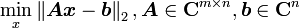
的特解为A的广义逆矩阵与b的乘积,这同时也是二范数极小的解,其通解为特解加上A的零空间。证明如下:
先将b拆成A的值域及其正交补两部分
所以 ,可得
,可得
故当且仅当 是
是 解时,
解时, 即为最小二乘解,即
即为最小二乘解,即 。
。
又因为
故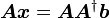 的通解为
的通解为
因为
所以 又是二范数极小的最小二乘解。
又是二范数极小的最小二乘解。














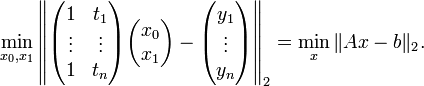
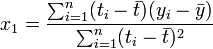
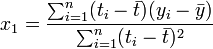
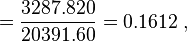














 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








