最近接下来几篇博文会回到神经网络结构的讨论上来,前面我在“深度学习方法(五):卷积神经网络CNN经典模型整理Lenet,Alexnet,Googlenet,VGG,Deep Residual Learning”一文中介绍了经典的CNN网络结构模型,这些可以说已经是家喻户晓的网络结构,在那一文结尾,我提到“是时候动一动卷积计算的形式了”,原因是很多工作证明了,在基本的CNN卷积计算模式之外,很多简化、扩展、变化都可以让卷积计算获得更多特性,比如参数减少,计算减少,效果提升等等。
接下来几篇文章会陆续介绍下面这些topic:
- Maxout Networks
- Network In Network
- Inception Net(Google)
- ResneXt
- Xception(depth-wise convolution)
- Spatial Transformer Networks
- …
本文先介绍两个13,14年的工作:Maxout Networks,Network In Network。网上有不少资料,但是很多作者我相信自己都没有完全理解,在本文中我会尽可能描述清楚。本文重点在于Network In Network。本文针对论文和网络资料的整理,自己重新撰写,保证每一个初学者都可以看懂。
1、Maxout Network
坦白说Maxout本身并不能算卷积结构的变化,但是它提出了一个概念——线性变化+Max操作可以拟合任意的的凸函数,包括激活函数(如Relu);后面要介绍的NIN有关系,所以先介绍一下Maxout。
Maxout出现在ICML2013上,大神Goodfellow(GAN的提出人~)将maxout和dropout结合后,号称在MNIST, CIFAR-10, CIFAR-100, SVHN这4个数据上都取得了start-of-art的识别率。
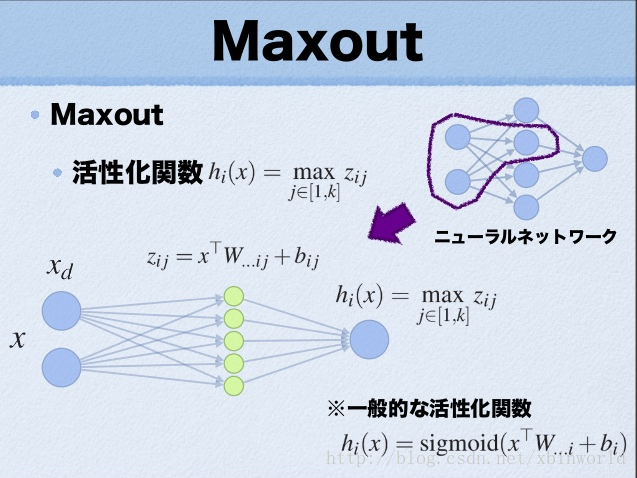
从论文中可以看出,maxout其实是一种激或函数形式。通常情况下,如果激活函数采用sigmoid函数的话,在前向传播过程中,隐含层节点的输出表达式为:
一般的MLP就是这样情况。其中W一般是2维的,这里表示取出的是第i列(对应第i个输出节点),下标i前的省略号表示对应第i列中的所有行。如果是maxout激活函数,则其隐含层节点的输出表达式为:
这里的W是3维的,尺寸为d*m*k,其中d表示输入层节点的个数,m表示隐含层节点的个数,k表示每个隐含层节点展开k个中间节点,这k个中间节点都是线性输出的,而maxout的每个节点就是取这k个中间节点输出最大的那个值。参考一个日文的maxout ppt 中的一页ppt如下:
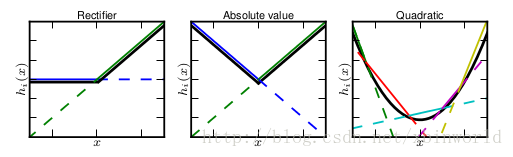
这张图的意识是说,紫圈中的隐藏节点展开成了5个黄色节点,取max。Maxout的拟合能力是非常强的,它可以拟合任意的的凸函数。从左往右,依次拟合出了ReLU,abs,二次曲线。
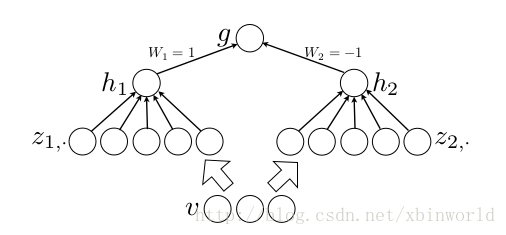
作者从数学的角度上也证明了这个结论,即只需2个maxout节点就可以拟合任意的凸函数了(相减),前提是中间节点的个数可以任意多,如下图所示,具体可以翻阅paper[1]。maxout的一个强假设是输出是位于输入空间的凸集中的….这个假设是否一定成立呢?虽然ReLU是Maxout的一个特例——实际上是得不到ReLU正好的情况的,我们是在学习这个非线性变换,用多个线性变换的组合+Max操作。
2、Network In Network
OK,上面介绍了Maxout[1],接下来重点介绍一下14年新加坡NUS颜水成老师组的Min Lin一个工作Network In Network ,说实话,不论是有心还是无意,本文的一些概念,包括1*1卷积,global average pooling都已经成为后来网络设计的标准结构,有独到的见解。
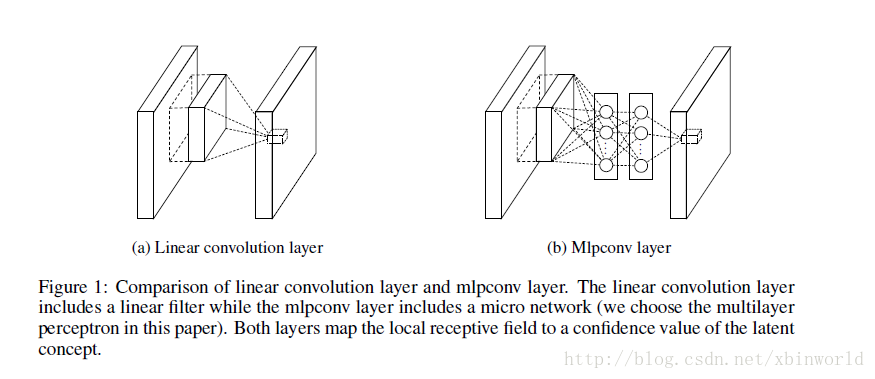
图1
先来看传统的卷积,图1左:
很多同学没有仔细看下标的含义,所以理解上模棱两可。xij表示的是一个卷积窗口的patch(一般是k_h*k_w*input_channel),k表示第k个kernel的index;激活函数是ReLU。并不是说只做一个kernel,而是指任意一个kernel。
再来看本文提出的Mlpconv Layer,也就是Network In Network,图1右。这里只是多加了一层全连接MLP层,什么意思呢?作者称之为“cascaded cross channel parametric pooling layer”,级联跨通道的带参数pooling层,目的是:
Each pooling layer performs weighted linear recombination on the input feature maps
看公式2就很清楚了,是第一层还是传统的卷积,在做一次卷积以后,对输出feature map的中的每一个像素点fij,其对应的所有channel又做了一次MLP,激活函数是ReLU。n表示第n层,而kn表示一个index,因为在第n层里面有很多kernel,和前面公式1是一个道理。所以,我们看下面整个NIN网络就很清楚了:
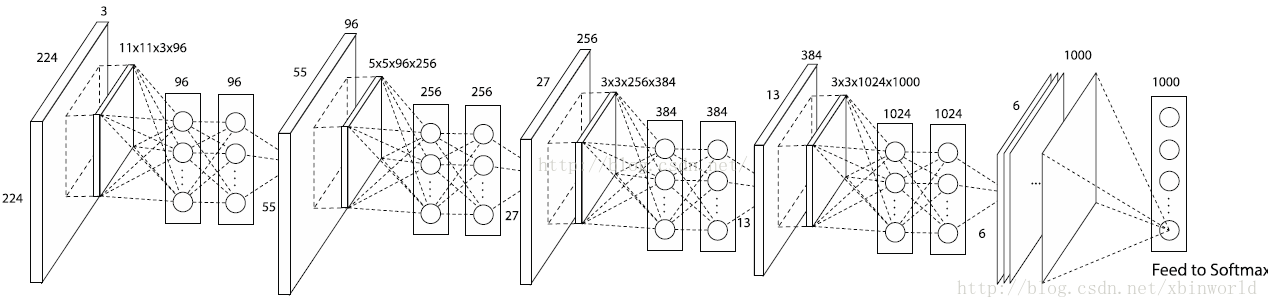
看第一个NIN,本来11*11*3*96(11*11的卷积kernel,输出map 96个)对于一个patch输出96个点,是输出feature map同一个像素的96个channel,但是现在多加了一层MLP,把这96个点做了一个全连接,又输出了96个点——很巧妙,这个新加的MLP层就等价于一个1 * 1 的卷积层,这样在神经网络结构设计的时候就非常方便了,只要在原来的卷积层后面加一个1*1的卷积层,而不改变输出的size。注意,每一个卷积层后面都会跟上ReLU。所以,相当于网络变深了,我理解其实这个变深是效果提升的主要因素。
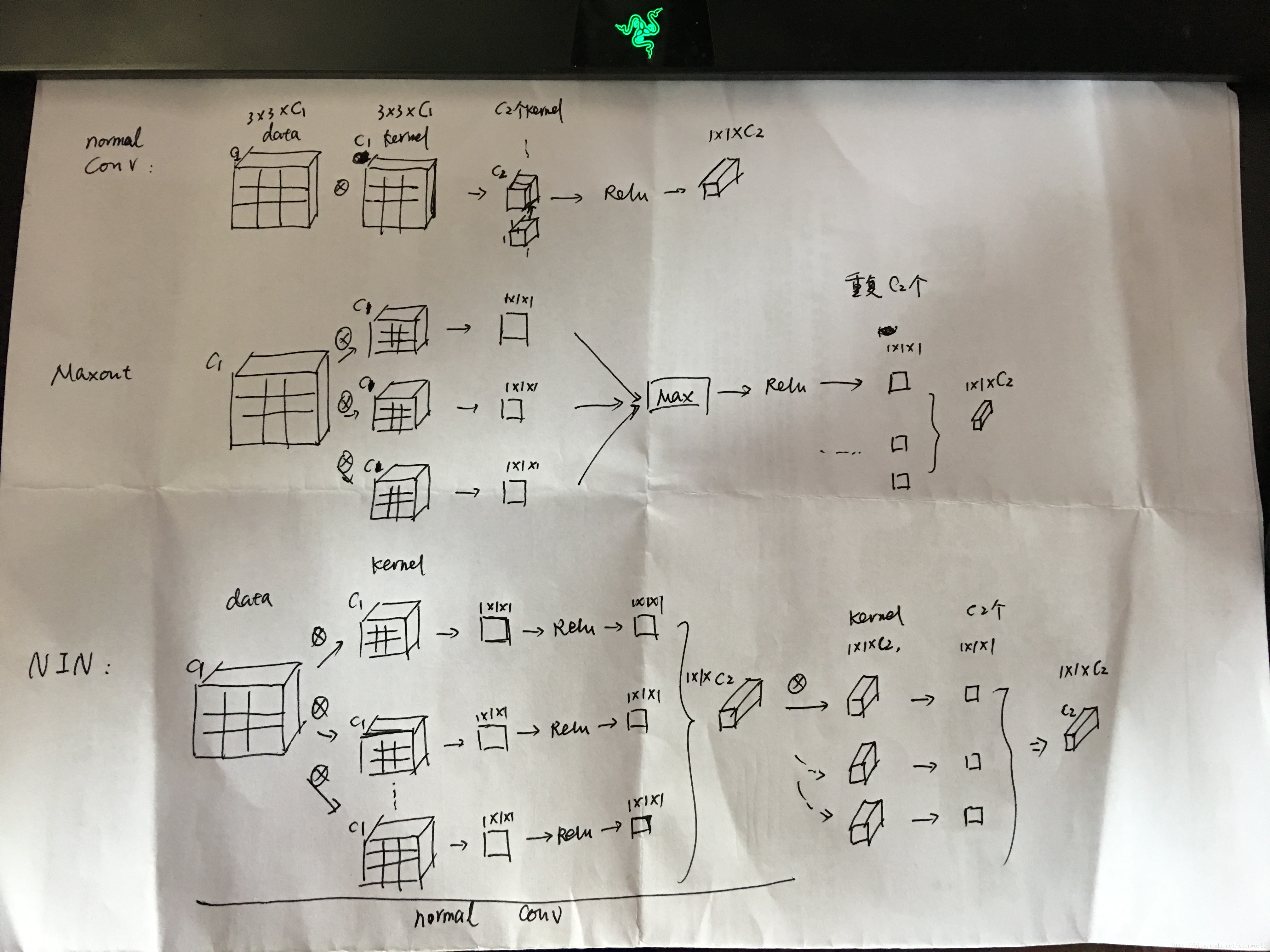
举例解释
假设现在有一个3x3的输入patch,用x代表,卷积核大小也是3x3,向量w代表,输入channel是c1,输出channel是c2。下面照片是我自己手画的,比较简单,见谅:)
- 对于一般的卷积层,直接x和w求卷积,得到1*1的1个点,有C2个kernel,得到1*1*c2;
- Maxout,有k个的3x3的w(这里的k是自由设定的),分别卷积得到k个1x1的输出,然后对这k个输入求最大值,得到1个1*1的点,对每一个输出channel都要这样做;
- NIN,有k个3x3的w(这里的k也是自由设定的),分别卷积得到k个1x1的输出,然后对它们都进行relu,然后再次对它们进行卷积,结果再relu。(这个过程,等效于一个小型的全连接网络)
这里建立了一个概念,全连接网络可以等价转换到1*1的卷积,这个idea在以后很多网络中都有用到,比如FCN[5]。
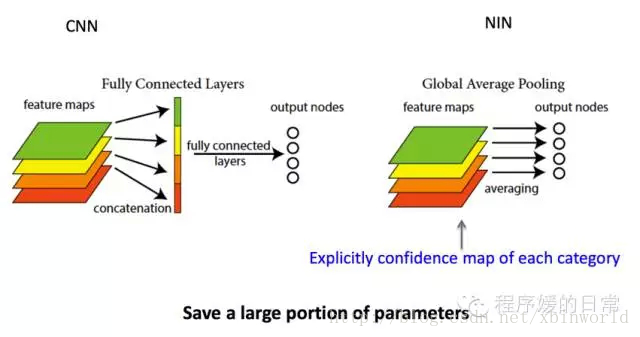
Global Average Pooling
在Googlenet网络中,也用到了Global Average Pooling,其实是受启发于Network In Network。Global Average Pooling一般用于放在网络的最后,用于替换全连接FC层,为什么要替换FC?因为在使用中,例如alexnet和vgg网络都在卷积和softmax之间串联了fc层,发现有一些缺点:
(1)参数量极大,有时候一个网络超过80~90%的参数量在最后的几层FC层中;
(2)容易过拟合,很多CNN网络的过拟合主要来自于最后的fc层,因为参数太多,却没有合适的regularizer;过拟合导致模型的泛化能力变弱;
(3)实际应用中非常重要的一点,paper中并没有提到:FC要求输入输出是fix的,也就是说图像必须按照给定大小,而实际中,图像有大有小,fc就很不方便;
作者提出了Global Average Pooling,做法很简单,是对每一个单独的feature map取全局average。要求输出的nodes和分类category数量一致,这样后面就可以直接接softmax了。
作者指出,Global Average Pooling的好处有:
- 因为强行要求最后的feature map数量等于category数量,因此feature map就会被解析为categories confidence maps.
- 没有参数,所以不会过拟合;
- 对一个平面的计算,使得利用了空间信息,对于图像在空间中变化更鲁棒;
Dropout
最后稍微提一下dropout,这个是hinton在Improving neural networks by preventing co-adaptation of feature detectors[9]一文中提出的。方法是在训练时,一层隐藏层输出节点中,随机选p(比如0.5)的比例的节点输出为0,而与这些0节点相连的那些权重在本次迭代training中不被更新。Dropout是一个很强力的正则方法,为啥?因为有一部分权重没有被更新,减少了过拟合,而且每一次训练可以看做使用的网络model是不一样的,因此,最终全局就相当于是指数个model的混合结果,混合模型的泛化能力往往比较强。一般Dropout用于FC层,主要也是因为FC很容易过拟合。








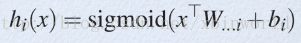
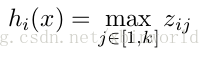
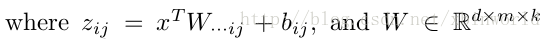

















 1292
1292

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








