两轮差速运动模型推导过程

        下面这张图片是从网络上拷贝过来，以这张图片为模型，我们来一步一步论证推导两轮差速运动模型，以下是原来网络上对这张图片的描述。
        下图是移动机器人在两个相邻时刻的位姿，其中 是两相邻时刻移动机器人绕圆弧运动的角度， 是两相邻时刻移动机器航向角（朝向角head）的变化量。 是左右轮之间的间距， 是右轮比左轮多走的距离。 是移动机器人圆弧运动的半径。

       从以上描述中我们得到一些定义：

1. 航向角α：           轮子行进方向与X轴夹角
2. 运动半径r1：      以两轮子轴心连线中点作为起点，沿着两轮子轴心连线的向量
3. θ3:                     相邻时刻两轮子航向角的增量
4. L：                     左右两轮的间距

        网络描述中d的定义有些狭隘，我们不使用它的定义，使用一些新的定义。按照常理，两轮子顺时针旋转，小车前进，两轮子逆时针旋转，小车后退，我们按照这个习惯，定义轮子顺时针为正方向，逆时针为负方向。同时我们定义初始状态下，距离原点最近的轮子为左轮，另外一个轮子为右轮

1. M(x,y)： 两轮子轴心连线中点
2. A(Xl,Yl):    左轮坐标
3. B(Xr,Yr）:右轮坐标
4. ω：    轮子角速度，ω1表示左轮角速度，ω2表示右轮角速度，顺时针为正
5. V：     轮子线速度，V1表示左轮线速度，V2表示右轮线速度
6. r：       轮子半径两轮半径一致

定义θ为X轴单位向量旋转θ角度后跟向量平行所得，以逆时针旋转为正方向，则

由几何关系分析可知：任意时刻
         
 

定义为B点的速度，同理定义β为X轴单位向量旋转β角度后跟向量平行所得，以逆时针旋转为正方向，因为任意时刻 ⊥ 则，已知B点角速度为ω1，由几何关系分析可知：任意时刻

 

定义 为A点的速度，同理定义Ф为X轴单位向量旋转Ф角度后跟向量 平行所得，同理

 

 
由于点M(x,y)为线段AB中点，所以m点速度为

Vm = (V1+ V2)/2 = ( -(ω1+ω2)*r* sinθ), (ω1+ω2)*r* cosθ)

假定在时刻t，左轮角速度为ωt1，右轮角速度为ωt2，经过时间Δt，当Δt→0时有：

因为任意时刻，两轮子的速度方向平行于同一直线，所以，M点线速度

左轮的运动弧长

右轮的运动弧长

由几何学分析我们可以得到，向量AB 与X轴单位向量的夹角θ的增量

由几何学分析已知，向量 与X轴单位向量的夹角θ的增量与航向角的增量任意时刻都相等相等，所以,t时刻，M点角速度为

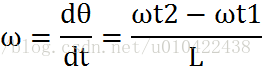
所以，时刻t，M点运动半径

                     

假定M点初始坐标为（a，b）,初始状态下X轴单位向量旋转β角度后与 平行，则

 

M点轨迹参数方程为，