73. Set Matrix Zeroes

题目大意：
给出一个m * n的矩阵，如果矩阵中的某个元素为0，则将该元素所在的整行和整列设为0，要求空间复杂度为O(1)，举个栗子：

 [0,1,2,3]      [0,0,0,0]
 [4,5,6,7]  ->  [0,5,6,7]
 [8,9,1,2]      [0,9,1,2]    

思路：
如果放宽对空间复杂度的限制，可以将原始矩阵复制一份，一边遍历原始矩阵，一边修改复制矩阵，这样的空间复杂度为O(mn)。

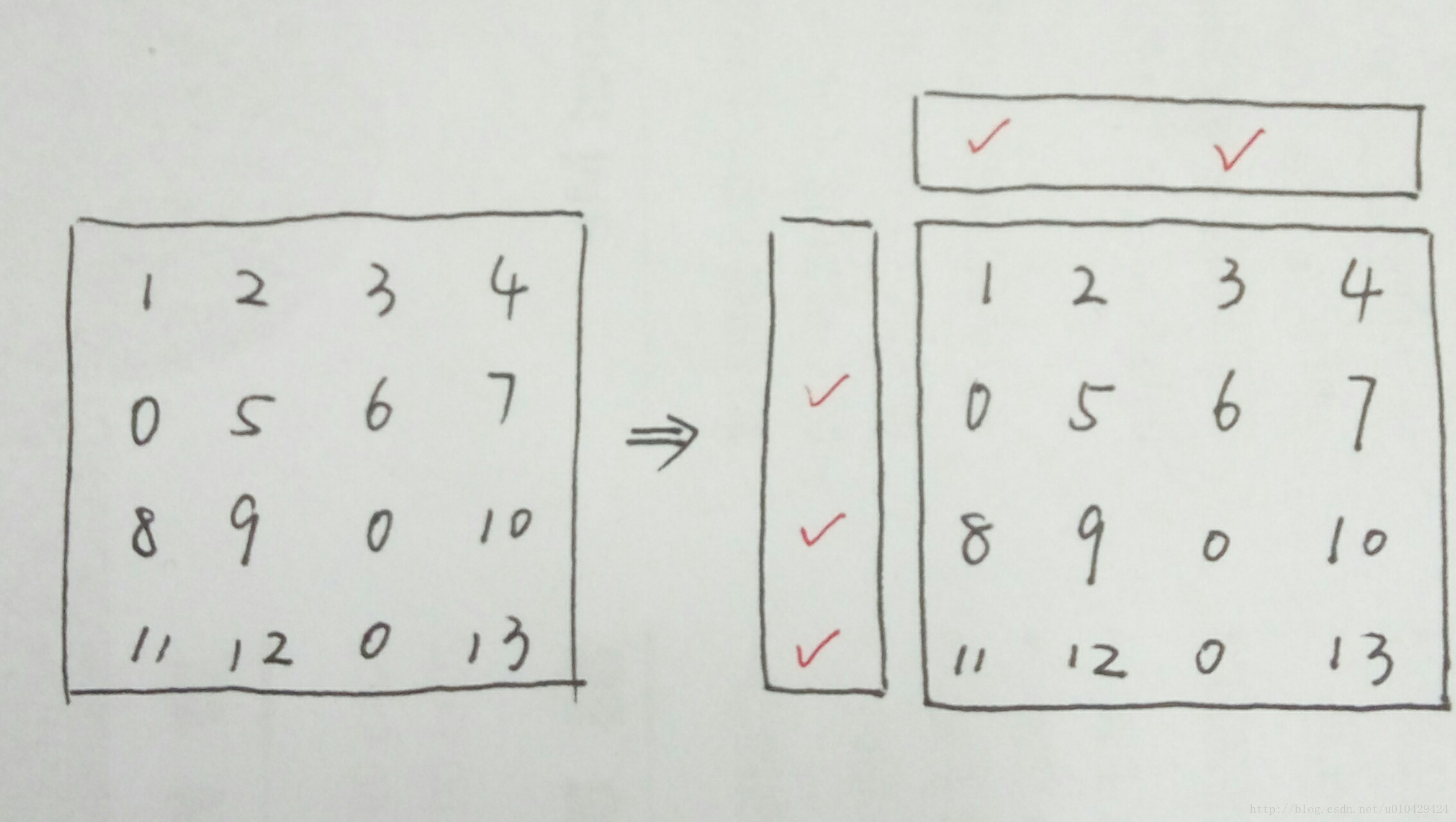
再优化一下，开辟一个大小为m的列表和一段大小为n的列表，m是矩阵的行数， n是矩阵的列数。如果(i,j)位置为0，将 i 保存到大小为m的列表中（m列表），将 j 保存到大小为n的列表中（n列表）。这样，相当于添加了标志位，m列表中标志哪一行要整行变为0，n列表中标志哪一列要整列变为0。这种方法的空间复杂度为O(m+n)。

当然，还可以再优化一下，不必额外开辟m + n的空间，充分利用矩阵的空间，将第一列和第一行作为m列表和n列表。

Python代码如下：

class Solution(object):
    def setZeroes(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        first_row = False
        first_col = False
        rows = len(matrix)
        cols = len(matrix[0])
        
        # 遍历第一行
        for i in range(cols):
            if matrix[0][i] == 0:
                first_row = True
                break
               
        # 遍历第一列
        for i in range(rows):
            if matrix[i][0] == 0:
                first_col = True
                break
        
        for i in range(1, rows):
            for j in range(1, cols):
                if matrix[i][j] == 0:
                    matrix[i][0] = 0
                    matrix[0][j] = 0
        
        for i in range(1, rows):
            for j in range(1, cols):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0
        
        if first_row:
            for i in range(cols):
                matrix[0][i] = 0
                    
        if first_col:
            for i in range(rows):
                matrix[i][0] = 0
                
# matrix = [
#     [0,2,3,4],
#     [5,6,7,0],
#     [9,10,11,12]    
# ]

# matrix= [
#     [0,1,1,5],
#     [4,3,1,4],
#     [0,1,1,4],
#     [1,2,1,3],
#     [0,1,1,1]
# ]

# matrix = [
#     [1],
#     [0]
# ]


matrix = [
    [-4, -21, 6, -7, 0],
    [-8, 6,  -8, -6, 0],
    [21, 2,  -9, -6,-10]
]

Solution().setZeroes(matrix)
# print()
for i in range(len(matrix)):
    for j in range(len(matrix[0])):
        print(matrix[i][j],' ', end = '')
    print()