重现二叉搜索树递归构建的过程

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

简单而言就是
左边的小于中间
中间的小于右边

首先建立几个数据变量

#define TYPE int

struct TreeNode;
typedef struct TreeNode* bst;
struct TreeNode
{
 TYPE data;
 SearchTree left;
 SearchTree right;
};

对于这种树，我们假设这棵树已经建好
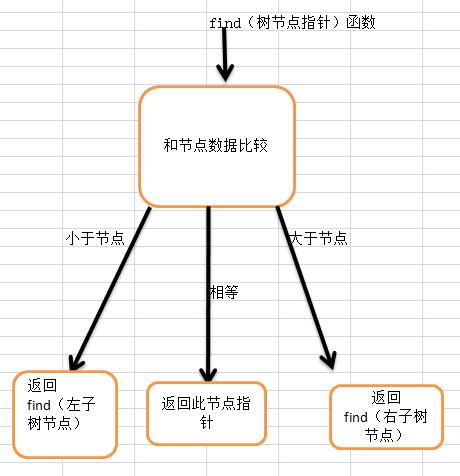
如何找到节点的数据，即搜索数据，并将节点指针返回
树的最本质的一种方法就是递归，对归只要拿出一种情况观察就可以
如下

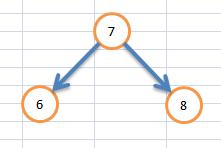
伪代码为
bst find（data，bst t）
{
    if(t == NULL)
        return NULL;
    if（data == t->data）
        return t;
    else
        if(data < t->data)
            return find(t->left);
        else
            return find(t->right);
}

这种find的搜索思想贯穿搜索树的操作
下面看看 怎么去建立一颗bst

比如对一串数
1 3 2 8 9 4 1
在建树的同时也是在排序的过程
首先有一颗树，然后将这些数字放进去

第一步就是建一颗小树
那么就以第一个数1为数据，下面是伪代码
bst t=malloc（）；
t-data=1；
t->left =NULL;
t->right =NULL;

第二步就是将数插入这个小树中

基本思想还是
比节点小的往左子树插
比节点大的往右子树插

首先函数的参数 肯定有x（要插入的数），二叉查找树的root指针 bst T
insert（bst T，x）
那么分这几种情况讨论
1、

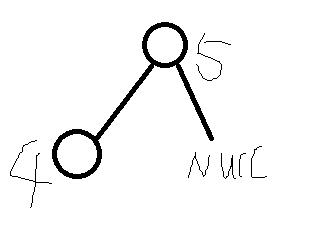
往这颗树T要插入6，insert（6，T）；
先比较节点数据5，发现大于5，则6要往右子树里面插
递归调用
insert（6，T->right）
此时6就应该插入在这里
而在这里的结束的条件是，传进来的树指针是NULL
所以

伪代码
if(T == NULL)
{
 T = malloc();
 T->data = x;
 T->left = NULL;
 T->right = NULL:
}

但是这时候有个问题
即我们在堆中开辟了新的空间，是需要将这个空间指针以链表形式连接到节点5上的，所以必然要返回一个树指针
所以 insert重新修改为
bst insert（x，bst T）
上面的伪代码也要将T返回

bst insert（x，bst T）
{
 if(T == NULL)
 {
  T = malloc();
  T->data = x;
  T->left = NULL;
  T->right = NULL:
 }

 return T;
}

基本调用为

main()
{
 bst T;  //已经初始化
 T->right=insert(6,T->right);
}

2、

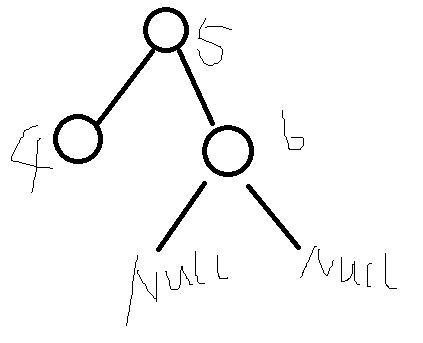
要往上面这颗树中插入8
同样是比较，情况1是这个递归结束的条件
那么用else分支进行递归
伪代码框架为

bst insert（x，bst T）
{
 if(T == NULL)
 {
  T = malloc();
  T->data = x;
  T->left = NULL;
  T->right = NULL:
 }
 else
 {
  if(T->data > x)
  {
       T->left=insert（x，T->left）；
  }
  else if(T->data <x)
  {
       T->right=insert（x，T->right）；
  }
 }

 return T;
}

所以二叉搜索树的插入也就完成了

---

为此完成一道题目

输入:
开始一个数n，(1<=n<=20) 表示有n个需要判断，n= 0 的时候输入结束。
接下去一行是一个序列，序列长度小于10，包含(0~9)的数字，没有重复数字，根据这个序列可以构造出一颗二叉搜索树。
接下去的n行有n个序列，每个序列格式跟第一个序列一样，请判断这两个序列是否能组成同一颗二叉搜索树。
输出:
如果序列相同则输出YES，否则输出NO
样例输入:
2
567432
543267
576342
0
样例输出:
YES
NO

基本思路就是 将这三棵树构建起来，
然后重新前序遍历，相同则是同一棵树

代码

#include <iostream>
#include <algorithm>
#include <string>


using namespace std;

#define TYPE int




struct TreeNode;

typedef struct TreeNode* SearchTree; 
typedef struct TreeNode* Position; 

struct TreeNode
{
    TYPE data;
    SearchTree left;
    SearchTree right;
};

/*
SearchTree
MakeEmpty(SearchTree T)
{
    if(T != NULL)
    {
        MakeEmpty(T->left);
        MakeEmpty(T->right);
        free(T);
    }
    return NULL;
}

Position
Find(TYPE x,SearchTree T)
{
    if(T=NULL)
        return NULL;
    if(x < T->data)
        return Find(x,T->left);
    else
        if(x > T->data)
            return Find(x,T->right);
        else
            return T;
}

Position
Findmin(SearchTree T)
{
    if(T == NULL)
        return NULL;
    else
        if(T->left == NULL)
            return T;
        else
            return Findmin(T->left);
}


Position
Findmax(SearchTree T)
{
    if(T == NULL)
        return NULL;
    else
        if(T->right == NULL)
            return T;
        else
            return Findmax(T->right);
}
*/
SearchTree
Insert(TYPE x,SearchTree T)
{
    if(T == NULL)
    {
        T = (SearchTree)malloc(sizeof(struct TreeNode));
        if(T == NULL)
            exit(-1);
        else
            T->data = x;
            T->left = NULL;
            T->right= NULL;
    }
    else if(x < T->data)
        T->left = Insert(x,T->left);
    else if(x > T->data)
        T->right = Insert(x,T->right);
    return T;
}


void DLR(SearchTree T,string& s)
{
    if(T!=NULL)
    {
        s.push_back(T->data);
        cout<<T->data<<endl;
        DLR(T->left,s);
        DLR(T->right,s);
    }

}

int main()
{   
    int b[]={5,6,7,4,3,2};
    int a[]={5,4,3,2,6,7};
    int c[]={5,7,6,3,4,2};
    string sb;
    string sa;
    string sc;
    SearchTree Tb=NULL;
    SearchTree Ta=NULL;
    SearchTree Tc=NULL;

    for(int i=0;i<6;++i)
    {
        Tb=Insert(b[i],Tb);
        Ta=Insert(a[i],Ta);
        Tc=Insert(c[i],Tc);
    }
    DLR(Tb,sb);
    DLR(Ta,sa);
    DLR(Tc,sc);

    if(sb==sa)
        cout<<"Yes"<<endl;
    else
        cout<<"No"<<endl;
    if(sb==sc)
        cout<<"Yes"<<endl;
    else
        cout<<"No"<<endl;

    return 0;
}