图论中最小生成树的问题学习

之前的博客分析过这种问题，并使用伪代码分析过其实现。
首先给出问题背景吧，其实岛屿问题（华为的机试题），要在n个岛屿上之间建桥，要使得所有岛屿联通，因为岛屿之前的距离不一样，所以规划出最短的造桥路径。
为了方便研究，从最简单的三个节点开始

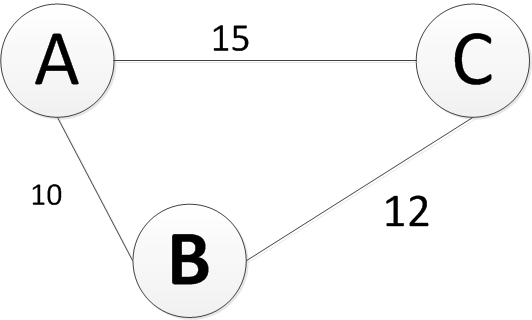
ABC三个岛屿，两两之间的距离如上图。
首先要将这种图的关系存储起来，要用到二维数组

#define N 3
int g[N][N];

图中的关系输入格式为
0 10 15
10 0 12
15 12 0
岛A到A的距离为0；
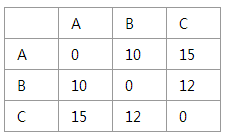
得到的一张二维数组表为

先学习一下别人的算法吧；
别人的源码

#include <stdio.h>
#include <string.h>
#define MaxInt 0x3f3f3f3f
#define N 110
//创建map二维数组储存图表，low数组记录每2个点间最小权值，visited数组标记某点是否已访问
int map[N][N],low[N],visited[N];
int n;

int prim()
{
    int i,j,pos,min,result=0;
    memset(visited,0,sizeof(visited));
//从某点开始，分别标记和记录该点
    visited[1]=1;pos=1;
//第一次给low数组赋值
    for(i=1;i<=n;i++)
        if(i!=pos) low[i]=map[pos][i];
//再运行n-1次
    for(i=1;i<n;i++)
    {
//找出最小权值并记录位置
     min=MaxInt;
     for(j=1;j<=n;j++)
         if(visited[j]==0&&min>low[j])
         {
             min=low[j];pos=j;
         }
//最小权值累加
    result+=min;
//标记该点
    visited[pos]=1;
//更新权值
    for(j=1;j<=n;j++)
        if(visited[j]==0&&low[j]>map[pos][j])
            low[j]=map[pos][j];
    }
    return result;
}

int main()
{
    int i,v,j,ans;
    while(scanf("%d",&n)!=EOF)
    {
//所有权值初始化为最大
        memset(map,MaxInt,sizeof(map));
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
            {
                scanf("%d",&v);
                map[i][j]=map[i][j]=v;
            }
            ans=prim();
            printf("%d\n",ans);
    }
    return 0;
}

博主用了三个数组来记录相关数据
int map[N][N],low[N],visited[N];
map 很容易理解，就是二维数组表示图的相关关系。
low用于保存待选择的权值，
visited用于记录哪些点已经遍历过了

首先找到一个入口

//从某点开始，分别标记和记录该点
    visited[1]=1;pos=1;
//第一次给low数组赋值
    for(i=1;i<=n;i++)
        if(i!=pos) low[i]=map[pos][i];

从第一个节点入手，标记第一个节点，并将和第一个节点相连的数据保存到low中，
对应上面n=3的例子，将10和15保存到low中，并标记A的位置

//再运行n-1次
    for(i=1;i<n;i++)
    {
//找出最小权值并记录位置
     min=MaxInt;
     for(j=1;j<=n;j++)
         if(visited[j]==0&&min>low[j])
         {
             min=low[j];pos=j;
         }
//最小权值累加
    result+=min;
//标记该点
    visited[pos]=1;
//更新权值
    for(j=1;j<=n;j++)
        if(visited[j]==0&&low[j]>map[pos][j])
            low[j]=map[pos][j];
    }

这个代码段，很类似一个递归的过程，暂不关注循环几次。

//找出最小权值并记录位置
     min=MaxInt;
     for(j=1;j<=n;j++)
         if(visited[j]==0&&min>low[j])
         {
             min=low[j];pos=j;
         }

这段代码就是，找出刚刚保存权值里面最小的一个
对应n=3的情况
min=10；
10对应的节点是B。pos指向B

//最小权值累加
    result+=min;
获取这个最小权值，

//标记该点
    visited[pos]=1;

将上面的最小权值对应的节点B，加入到visited，就是标记起来

//更新权值
    for(j=1;j<=n;j++)
        if(visited[j]==0&&low[j]>map[pos][j])
            low[j]=map[pos][j];

然后将B相连的权值加入到low中，
此时对应n=3情况为
\
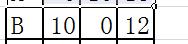
此时有个问题就是，前面最小的权值是10，需要将这个权值从low中去除掉，
看看这个他是怎么做到的
他并没有这样做，因为用min保存了这个最小的权值，下次只要和这个变量比就可以了，
而是去更新和同一个节点连接的最小的权值，
首先A和B节点都已经标记，所以到达A和B节点的权值已经确定，现在是到达C节点的权值要求最小，而low中下标3就是c节点对应的，权值存放区，所以更新之后，再找出最小权值。

然后利用for进行循环，
如果有n个节点，那么就需要找出n-1个最小权值，

这种思想是可以的，现在看看 能不能修改利用 priority_queue来完成上面的工作，
初步代码是这样的

int myalgo(int g[3][3],int num)
{
 int i=0;
 int j=0;
 int min=0;
 int cnt;
 type_chose buff;
 priority_queue <type_chose> chose;
 vector <int> flag_node;
 flag_node.resize(num);

 //enter loc 0;
 int loc=0;
 flag_node[loc]=1;

 for(i=0;i<num;++i)
 {
  if(i!=loc)
  {
   buff.dis=g[loc][i];
   buff.num=i;
   chose.push(buff);
  }
 }

 for(j=0;j<num-1;++j)
 {


  min+=chose.top().dis;
  loc=chose.top().num;
  chose.pop();

  flag_node[loc]=1;

  for(i=0;i<num;++i)
  {
   if(flag_node[i]==0)
   {
    buff.dis=g[loc][i];
    buff.num=i;
    chose.push(buff);
   }
  }
 }

 return min;

}

本来想利用有限队列来完成寻找最小权值，但是出现一个问题就是，
优先队列只能删除top元素，而不能删除特定的元素，因为在最小生成树中需要删除特定元素。

参考资料
http://www.cnblogs.com/Veegin/archive/2011/04/29/2032388.html