梯度下降

最新推荐文章于 2022-08-29 15:14:12 发布

爱科研的徐博士

最新推荐文章于 2022-08-29 15:14:12 发布

阅读量1.5k

点赞数

分类专栏：【算法】优化方法文章标签：函数优化梯度下降随机梯度下降 Python实现

本文链接：https://blog.csdn.net/u010626937/article/details/74940859

版权

【算法】优化方法专栏收录该内容

6 篇文章 1 订阅

订阅专栏

问题的引入

我们知道导数的求导公式为：

由公式可见，对点x0的导数反映了函数在点x0处的瞬时变化速率，或者叫在点x0处的斜度。这是对于一维函数来说，如果推广到多维函数中，就有了梯度的概念，梯度是一个向量组合，反映了多维图形中变化速率最快的方向。

我们先对单个特征 $\Theta _{1}$ 进行分析。我们先从实际问题引入。在此处，为了简单，假设我们的房屋就是一个变量影响的，就是房屋的面积。假设有一个房屋销售的数据如下：

面积（m^2）	销售价钱（万元）
123	250
150	320
102	220
87	160
…	…

现在我们可以画出一个三点分布图，x轴是房屋面积，y轴是房屋售价。

如果一个新的房子面积，假设在销售价钱的记录中没有，我们该怎么估价呢？
我们可以用一条直线或者曲线去尽量准的拟合这些已有的数据，然后如果有新的数据输入过来，我们可以曲线上这个点的值返回。如果我们用一条直线来拟合本例中的数据，可能是下面这个样子：

假设，新来一个数据：房子面积为：150m^2，那么下图中的绿色点所对应的y值就是我们要返回的值。

上例中我们拟合出的直线函数可以称为线性回归函数，如果我们设房屋面积为x，则此线性回归函数可写为：

$f(x)=\Theta x$
$\Theta$ 称为参数。

但是在实际生活中，房子的价格肯定不会只和房屋的面积有关系。我们可以用x1,x2,…Xn去描述feature里面的分量，比如，x1=房间的面积，x2=房间的朝向，等等，我们可以做出一个估计函数：

θ在这儿称为参数，在这儿的意思是调整feature中每个分量的影响力，就是到底是房屋的面积更重要还是房屋的地段更重要。如果我们令X0 = 1，就可以用向量的方式来表示了：

在本式子中， $\Theta^{T},X$ 都表示向量，我们程序也需要一个机制去评估我们θ是否比较好，所以说需要对我们做出的h函数进行评估，一般这个函数称为损失函数（loss function）或者错误函数(error function)，描述h函数不好的程度，在下面，我们称这个函数为J函数。

在此，我们假设拟合函数和梯度函数为：

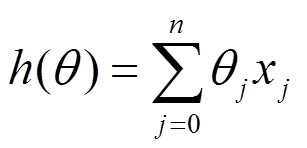
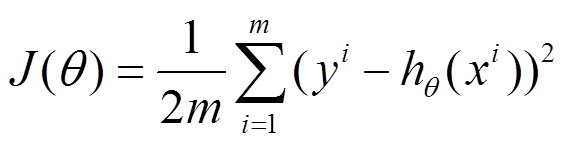
PS:n:为特征数，m:为样本数。有的资料上面J(θ)的系数是乘以1/2，在这里我们乘的是1/(2m),这是不受影响的。

如何调整θ以使得J(θ)取得最小值有很多方法，其中有最小二乘法(min square)，是一种完全是数学描述的方法，在stanford机器学习开放课最后的部分会推导最小二乘法的公式的来源，这个来很多的机器学习和数学书上都可以找到，这里就不提最小二乘法，而谈谈梯度下降法。

梯度下降法是按下面的流程进行的：

1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

深度理解

问题求解

在本节中我们以简单的线性回归函数为例进行分析。对于上一部分讲到的线性回归，先化一个为一个特征θ1，θ0为偏置项，最后列出的误差函数如下图所示：

目标是优化J(θ1)，得到其最小化，下面给出TrainSet，{(1,1),(2,2),(3,3)}通过手动寻找来找到最优解，由图可见当θ1取1时，与y(i)完全重合，J(θ1) = 0.

下面是θ1的取值与对应的J(θ1)变化情况

由此可见，J（theta）的最优解即为0，现在来看通过梯度下降法来自动找到最优解，对于上述待优化问题，下图给出其三维图像，可见要找到最优解，就要不断向下探索，使得J(θ)最小即可。

梯度下降的几何形式

为了更清晰，先给出下面的图像。

这是一个表示参数θ与误差函数J(θ)的关系图，红色部分是表示J(θ)有着比较高的取值，我们需要的是，能够让J(θ)的值尽量的低。也就是深蓝色的部分。θ0，θ1表示θ向量的两个维度。

在上面提到梯度下降法的第一步是给θ给一个初值，假设随机给的初值是在图上的十字点。

然后我们将θ按照梯度下降的方向进行调整，就会使得J(θ)往更低的方向进行变化，如图所示，算法的结束将是在θ下降到无法继续下降为止。

当然，可能梯度下降的最终点并非是全局最小点，可能是一个局部最小点，可能是下面的情况：

上面这张图就是描述的一个局部最小点，这是我们重新选择了一个初始点得到的，看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点。

其实，J(θ)的真正图形是类似下面这样的，因为其是一个凸函数（在本例中），只有一个全局最优解，所以不必担心像上图一样找到局部最优解。

沿着梯度下降的方向，自动求解最小值的方法就是所谓的梯度下降法。

对参数向量θ中的每个分量θj，迭代减去速率因子a* (dJ(θ)/dθj)即可，后边一项为J(θ)关于θj的偏导数。

对于我们的函数J(θ)求关于θj的偏导数:

$\frac{\partial }{\partial \theta_{j} }J(\theta )=\frac{\partial }{\partial \theta_{j} }\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x^{i}_{j}$

下面是更新的过程，也就是θj会向着梯度最小的方向进行减少。θj表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

$\theta '_{j}=\theta _{j}+\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x^{i}_{j}$

从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了后面将要介绍的另外一种方法，随机梯度下降。而此时我们介绍的方法常被称为批量梯度下降法。

一个很重要的地方值得注意的是，梯度是有方向的，对于一个向量θ，每一维分量θi都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。

倒三角形表示梯度，按这种方式来表示，θi就不见了，看看用好向量和矩阵，真的会大大的简化数学的描述啊。

下图展示了对单个特征θ1的直观图形，当导数为正时，θ1减小后并以新的θ1为基点重新求导，一直迭代就会找到最小的θ1，若导数为负时，θ1的就会不断增到，直到找到使损失函数最小的值。

有一点需要注意的是步长a的大小，如果a太小，则会迭代很多次才找到最优解，若a太大，可能跳过最优，从而找不到最优解。

另外，如果在不断迭代的过程中，梯度值会不断变小，所以θ1的变化速度也会越来越慢，所以不需要使速率a的值越来越小

寻找过程如下图所示：

当梯度下降到一定数值后，每次迭代的变化很小，这时可以设定一个阈值，只要变化小鱼该阈值，就停止迭代，而得到的结果也近似于最优解。

eg:

若损失函数的值不断变大，则有可能是步长速率a太大，导致算法不收敛，这时可适当调整a值eg:

为了选择参数a，就需要不断测试，因为a太大太小都不太好。

随机梯度下降

在上一部分，已经提到过随机梯度下降，我们再重新回顾以及引出。

1、批量梯度下降的求解思路如下：

（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度

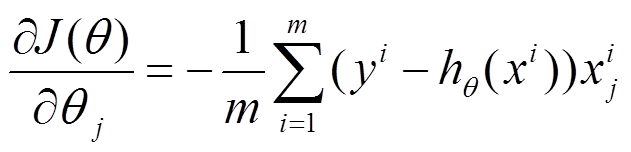
（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta

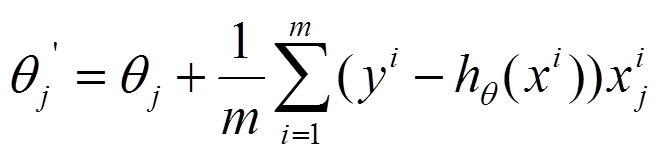
（3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了另外一种方法，随机梯度下降。

2、随机梯度下降的求解思路如下：

（1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本。

$J(\theta )=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$

$\frac{\partial }{\partial \theta _{j}}J(\theta )=(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}_{j}$

（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta.

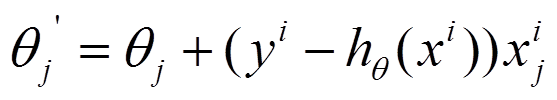
（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

3、对于上面的linear regression问题，与批量梯度下降对比，随机梯度下降求解的会是最优解吗？

（1）批量梯度下降—最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。

（2）随机梯度下降—最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

python实现

梯度下降算法的实现：

#-*- encoding:utf-8 -*-

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt


#构造训练数据集
x= np.arange(0.,10.,0.2)
m=len(x)
x0=np.full(m,1.0)#生成偏置bias，x0均为1
input_data=np.vstack([x0,x]).T,#将偏置bias作为权重向量的第一个分量
#print input_data
target_data=2*x+5+np.random.rand(m)
#print target_data


#两种终止条件
loop_max=10000
epsilon=1e-3
#print epsilon

#初始化权值
np.random.seed(0)
w=np.random.randn(2)
#print w

alpha=0.001#步长（注意取值过大会导致震荡，过小收敛速度变慢）
diff=0.
error=np.zeros(2)
count=0 #循环次数
finish=0 #终止标志
# --------------------------------梯度下降算法------------------------------
while count<loop_max:
    count +=1

    #标准梯度下降是在权重更新前对所有的样例汇总误差，而随机下降的权值是通过考察某个训练样例来更新的
    #标准梯度下降中，权重更新的每一步对多个样例求和，需要更多的计算
    sum_m=np.zeros(2)
    for i in range(m):
        dif=(np.dot(w,input_data[0][i,:])-target_data[i])*input_data[0][i,:]
        sum_m=sum_m+dif #当alpha取值过大的时候，sum_m会在迭代过程中溢出

    w =w-alpha*sum_m#注意步长的物质，过大会导致震荡
    #判断时候已经收敛：
    if np.linalg.norm(w-error)<epsilon:
        finish=1
        break
    else:
        error=w

print 'loop count=%d'%count,'\t w:[%f,%f]'%(w[0],w[1])

#check with scipy linear regression
slop,intercept,r_value,p_value,slope_std_error=stats.linregress(x,target_data)
print 'intercept=%s slope=%s'%(intercept,slop)

#通过结果可以观察到，随机梯度下降算法得到的intercept (w0)和slope(w1)和linear regression得到的很近

plt.plot(x,target_data,'k+')
plt.plot(x,w[1]*x+w[0],'r')
plt.show()

实验结果：

loop count=296   w:[5.296925,2.042263]
intercept=5.37420551187 slope=2.03046162353
finished need time: 0.056000 s

随机梯度下降算法：

-*- encoding:utf-8 -*-

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import time

#构造训练数据集
x= np.arange(0.,10.,0.2)
m=len(x)
x0=np.full(m,1.0)#生成偏置bias，x0均为1
input_data=np.vstack([x0,x]).T,#将偏置bias作为权重向量的第一个分量
#print input_data
target_data=2*x+5+np.random.rand(m)
#print target_data


#两种终止条件
loop_max=10000
epsilon=1e-3
#print epsilon

#初始化权值
np.random.seed(0)
w=np.random.randn(2)
#print w

alpha=0.01#步长（注意取值过大会导致震荡，过小收敛速度变慢）
diff=0.
error=np.zeros(2)
count=0 #循环次数
finish=0 #终止标志

t1=time.time()
#------------------------------随机梯度下降算法--------------------------------------
while count<loop_max:
    count+=1

    #遍历所有的训练数据集，不断更新权重
    for i in range(m):
        diff=np.dot(w,input_data[0][i,:])-target_data[i]#训练集带入，计算误差，
                                                   # 注意input_data的第一维为1，第二维为其真正的特征
                                                   #w的第一维为随机产生的bias值，第二维为其权值w1
        #采用随机梯度下降算法，更新一次权值只使用一组训练数据
        w=w-alpha*diff*input_data[0][i,:]

        #-----------------终止条件判断-----------------------------------
        #若没有终止，则继续读取样本进行处理，如果所有样本都读取完毕了，则循环重新从头开始读取样本进行处理

    #-----------------------------终止条件判断--------------------------------
    #注意：有多种迭代终止条件，和判断语句的位置。终止判断可以放在权值向量更新一次后，也可以放在更新m次后
    if np.linalg.norm(w-error)<epsilon:#终止条件：前后两次计算出的权向量的绝对误差充分小
        finish=1
        break
    else:
        error=w

t2=time.time()
print 'loop count=%d'%count,'\t w:[%f,%f]'%(w[0],w[1])



#check with scipy linear regression
slop,intercept,r_value,p_value,slope_std_error=stats.linregress(x,target_data)
print 'intercept=%s slope=%s'%(intercept,slop)
print 'finished need time: %f s'%(t2-t1)
#通过结果可以观察到，随机梯度下降算法得到的intercept (w0)和slope(w1)和linear regression得到的很近

plt.plot(x,target_data,'k+')
plt.plot(x,w[1]*x+w[0],'r')
plt.show()

实验结果：

loop count=63    w:[5.550357,2.006701]
intercept=5.56122633489 slope=1.99818270195
finished need time: 0.011000 s

实验结果还是比较明显的，随机梯度下降速度快，迭代次数少，但是这也取决于阈值的大小，如果阈值设的太小，随机梯度的优势也不是很明显。但是对于效果来讲，梯度（批量梯度）下降法要好于随机梯度下降法，所以，当数据量不是很大的时候，还是推荐使用批量梯度下降。但是在实际应用中，数据量都是比较大的，所以随机梯度的使用更加普遍。

参考文献：

1
2
3

《完》

所谓的不平凡就是平凡的N次幂。
                    ------By Ada

爱科研的徐博士

关注

0
点赞
踩
8

收藏

觉得还不错? 一键收藏
打赏
0
评论
梯度下降

问题的引入我们知道导数的求导公式为：由公式可见，对点x0的导数反映了函数在点x0处的瞬时变化速率，或者叫在点x0处的斜度。这是对于一维函数来说，如果推广到多维函数中，就有了梯度的概念，梯度是一个向量组合，反映了多维图形中变化速率最快的方向。我们先对单个特征进行分析。我们先从实际问题引入。在此处，为了简单，假设我们的房屋就是一个变量影响的，就是房屋的面积。假设有一个房屋销售的数据如下：面积
复制链接

扫一扫