deep learning中一些层的介绍和代码实现

文章来自：https://leonardoaraujosantos.gitbooks.io
原文作者：Leonardo Araujo dos Santos
公众号：机器学习算法工程师
https://blog.csdn.net/byplane/article/details/52422997
https://mp.weixin.qq.com/s/oFWqM9HPhstk7H-GQY0O3g
作者：石文华
编辑：田　旭
翻译

relu层

如何在Python中实现ReLU层？

简而言之，relu层就是输入张量通过一个非线性的relu函数，得到输出，而不改变其空间或者深度信息

从上图可以看出，所有大于0的保持不变，而小于零的变为零。此外，空间信息和深度也是相同的

relu函数作为激活函数，具有以下功能：

1.易于计算（前向/反向传播），采用sigmoid函数作为激活函数时候（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相当大，而采用Relu激活函数，整个过程的计算量节省很多。

2.深度模型中受消失梯度的影响要小得多，对于深层网络，sigmoid函数反向传播时，很容易就出现梯度消失的情况（在sigmoid函数接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练。

3.如果你使用大的学习率，他们可能会不可逆转地死去，因为当一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了。这个神经元的梯度将一直都是0了。

1、前向传播

将所有小于0的数变成0，大于0的数保持不变，空间和深度信息保持不变。

python实现relu的前向传播：

import numpy as np


def relu_forward(x):
    """
    Computes the forward pass for ReLU
    Input: - x: Inputs, of any shape

    Returns a tuple of :(out, cache)
    The shape on the output is the same as the input
    """
    relu = lambda x: x * (x > 0).astype(float)
    out = relu(x)
    # Cache input and return outputs
    cache = x
    return out, cache


if __name__ == "__main__":
    input_ = np.random.normal(loc=0.0, scale=1.0, size=10)
    print(input_)
    print("###########################################")
    print(relu_forward(input_))

2、反向传播

在前向传播的时候，我们对每个输入X=[x1,x2,x3]应用了max(0,x)函数，所以在反向传播的时候，小于0的元素,梯度dx等于0：

python实现relu 反向传播：

def relu_backward(dout, cache):
    """
    Computes the backward pass for ReLU
    Input:
        :param dout: Upstream derivatives(上游衍生品) ,of any shape
        :param cache: Previous input (used on forward propagation)
    :return:
        -dx: Gradient with respect to x
    """
    # Inititalize dx with None and x with cache
    dx, x = None, cache

    # Make all positive elements in x equal to dout while all the other elements
    dx = dout * (x >= 0)

    # Return dx (gradient with respect to x)
    return dx

Dropout层

Dropout是一种用于防止神经网络过度拟合的技术，你还可以使用L2正则化防止过拟合。

神经网路是怎么采用L2防止过拟合的呢？

下面是分类的错误率，可以发现使用了dropout之后错误率更低：

和其他正则化技术一样，使用dropout会使得训练损失稍稍恶化，但是模型的泛化能力却更好，因为如果我们的模型过于复杂（更多层或者更多神经元），模型就很可能过拟合，下面是训练和验证集上的损失情况，以及他们中有无dropout情况。

1、dropout工作原理

在训练期间，随机的选择一定比例的神经元，让它停止工作，如下图所示，这样泛化能力更好，因为你的网络层的不同的神经元会学习相同的“概念”。在测试阶段，不需要使用dropout.

2、在哪里使用dropout

通常会在全连接层使用dropout，但也可以在最大池化后使用dropout,从而产生某种图像噪声增强。

3、dropout的实现

为了实现某个神经元的失活，我们在前向传播过程中创建一个掩码(0和1)，此掩码应用于训练期间的层的输出，并缓存以供以后在反向传播中使用。如前所述，这个dropout掩码只在训练中使用。

在反向传播中，我们对被激活的神经元感兴趣(我们需要将掩码保存为前向传播)，这些被选中的神经元中，使用反向传播，失活的神经元没有可学习的参数，仅仅是输入x，反向传播返回dx。

4、dropout的功效

Dropout背后理念和集成模型很相似。在Drpout层，不同的神经元组合被关闭，这代表了一种不同的结构，所有这些不同的结构使用一个的子数据集并行地带权重训练，而权重总和为1。

如果Dropout层有 n 个神经元，那么会形成2^n个不同的子结构。在预测时，相当于集成这些模型并取均值。这种结构化的模型正则化技术有利于避免过拟合。

Dropout有效的另外一个视点是：由于神经元是随机选择的，所以可以减少神经元之间的相互依赖，从而确保提取出相互独立的重要特征。

5、python实现dropout的前向传播

import numpy as np


def dropout_forward(x, dropout_param):
    """
    Performs the forward pass for (inverted) dropout.
    :param x: Input data, of any shape
    :param dropout_param:  A dictionary with the following keys: (p, test/train,seed)
    :return: (out, cache)
    """
    # Get the current dropout mode, p, and seed
    p, mode = dropout_param['p'], dropout_param['mode']
    if 'seed' in dropout_param:
        np.random.seed(dropout_param['seed'])

    # Initialization of outputs and mask
    mask = None
    out = None

    if mode == 'train':
        # Create an apply mask (normally p=0.5 for half of neurons), we scale all
        # by p to avoid having to multiply by p on backpropagation, this is called
        # inverted dropout
        mask = (np.random.rand(*x.shape) < p) / p
        # Apply mask
        out = x * mask
    elif mode == 'test':
        # During prediction no mask is used
        mask = None
        out = x

    # Save mask and dropout parameters for backpropagation
    cache = (dropout_param, mask)

    # Convert "out" type and return output and cache
    out = out.astype(x.dtype, copy=False)
    return out, cache


if __name__ == "__main__":
    x = np.random.rand(3, 2)
    dropout_param = {'p': 0.5, 'mode': 'train', 'seed': 0}
    out, cache = dropout_forward(x, dropout_param)
    print(out)
    print('++++++++++++++++++++++++++++++++===')
    print(cache)

6、python实现dropout的反向传播

def dropout_backward(dout, cache):
    """
    Perform the backward pass for (inverted) dropout.
    :param dout: Upstream derivatives, of any shape
    :param cache: (dropout_param, mask) from dropout_forward.
    :return: dx
    """
    # Recover dropout parameters(p, mask, mode) from cache
    dropout_param, mask = cache
    mode = dropout_param['mode']

    dx = None
    # Back propagate(传播)(Dropout layer has no parameters just input X)
    if mode == 'train':
        # Just back propagate dout from the neurons that ware used during dropout
        dx = dout * mask
    elif mode == 'test':
        # Disable dropout during prediction/test
        dx = dout

    return dx

卷积层

简单的说，卷积层所做的工作就是对输入的特征图应用卷积算子，卷积核的个数是输出特征图的深度。下面我们介绍一下相关的参数：

• N:批处理大小(4d张量上的图像数)
• F:卷积层上的滤波器个数
• kW/kH:内核宽度/高度(通常我们使用方形卷积核，kW=kH)
• H/W:图像高度/宽度(通常H=W)
• H’/W’:卷积图像高度/宽度(如果使用适当的填充，则与输入相同)
• Stride:卷积滑动窗口将要移动的像素数。
• Padding:将0添加到图像的边框，以保持输入和输出大小相同。
• Depth:输入特征图的深度(如输入为RGB图像则深度为3)

1、前向传播

在前向传播过程中，我们用不同的过滤器“卷积”输入，每个过滤器将在图像上寻找不同的特征。

没有搞明白这个里面怎么体现不同卷积对应的不同特征的

2、python实现卷积层的前向传播

def conv_forward_naive(x, w, b, conv_param):
    """
    Computes the forward pass for the Convolution layer.(Naive)
    :param x: Input data of shape (N, C, H, W)
    :param w: Filter weights of shape(F, C, HH, WW)
    :param b: Biases, of shape(F,)
    :param conv_param:  A dictionary with the following keys:
        - 'stride': How much pixels the sliding window will travel
        - 'pad': The number of pixels that will be used to zero-pad the input.

    N: Mini-batch size
    C: Input depth(ie 3 for RGB images)
    H/W: Image height/width
    F: Number of filters on convolution layer (will be the output depth)
    HH/WW: Kernel Height/width

    :returns a tuple of:
        - out: Output data, of shape(N, F, H', W') where H' and W' are given by
            H' = 1 + (H + 2 * pad - HH)/stride
            W' = 1 + (W + 2 * pad - WW)/stride
        - cache: (x, w, b, conv_param)
    """
    out = None
    N, C, H, W = x.shape
    F, C, HH, WW = w.shape

    # Get parameters
    P = conv_param['pad']
    S = conv_param['stride']

    # Calculate output size, and initialization output volume
    H_R = 1 + (H + 2 * P - HH) / S
    W_R = 1 + (W + 2 * P - WW) / S
    out = np.zeros((N, F, H_R, W_R))

    # Pad images with zeros on the border (Used to keep spatial information)
    x_pad = np.lib.pad(x, ((0, 0), (0, 0), (P, P), (P, P)), 'constant', constant_values=0)

    # Apply the convolution
    for n in range(N):  # For each element on batch
        for depth in range(F):
            for r in range(0, H, S):  # Slide（滑动） vertically(垂直) taking stride into account
                for c in range(0, W, S):  # Slide horizontally(水平) taking stride into account
                    out[n, depth, r/S, c/S] = np.sum(x_pad[n, :, r, r+HH, c: c+WW] * w[depth, :, :, :]) + b[depth]

    # Cache parameters and inputs for back propagation and return output volume(卷积)
    cache = (x, w, b, conv_param)
    return out, cache

3、反向传播

为了更好的理解，这里使用1维卷积来理解卷积层的反向传播，2维的也类似。

输入信号为X=[x0,x1,x2,x3,x4],参数为W=[w0,w1,w2]，不使用padding，卷积之后的结果是：Y=[y0,y1,y2]，这里Y = X * flip(W)，flip可以看作是180度的旋转。

现在我们使用计算图来表示，并且加上一个偏差，通过观察可以发现这个过程跟全连接层类似，不同之处在于卷积核可以使得权重共享。

现在来看反向传播 ：

向后追踪计算图，反向传播可以表示为以下的公式：

$$\frac{\partial L}{\partial X}$$
意味着损失值随着输入进行变化，由上图可以看出。

注意：
dX跟X大小相同，所以我们需要进行填充
dout跟Y大小相同，在本例中为3（渐变输入）
为了节省编程工作量，我们将梯度的计算采用卷积的形式
在dX梯度上，所有元素都乘以W，所以我们可能会对W和dout进行卷积操作
1d卷积的输出尺寸计算公式：outputSize=(InputSize-KernelSize+2P)+1，
我们期望的尺寸是3，由于原始输入尺寸是3，并且我们将与也有3个元素的W矩阵进行卷积。所以我们需要用2个零填充输入，之后再进行卷积，就可以得到尺寸为3的输出。

就卷积而言：
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

根据链式法则，求损失函数对各个参数的偏导：
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

再次查看从图表中得到的表达式，可以将它们表示为dout和X之间的卷积。同样，由于输出将是3个元素，因此不需要进行填充。

就卷积的计算而言，
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$
如果将X看成是卷积核，而dout看做输入信号，则：

$$\frac{\partial L}{\partial W} = dout *X$$
对于偏差，计算将类似于全连接层。 基本上我们每个过滤器有一个偏差,计算如下：
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

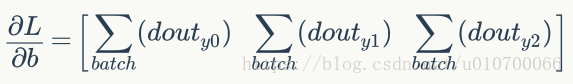
4、python实现卷积的反向传播

def conv_backward_naive(dout, cache):
    """
    Computes the backward for the Convolution layer.(Naive)
    :param dout: Upstream derivatives.
    :param cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive
    :returns: a tuple of： （dw, dx, db) gradients
    """
    dx, dw, db = None, None, None
    x, w, b, conv_param = cache
    N, F, H_R, W_R = dout.shape
    N, C, H, W = x.shape
    F, C, HH, WW = w.shape
    P = conv_param['pad']
    S = conv_param['stride']
    # Do zero padding on x_pad
    x_pad = np.lib.pad(x, ((0, 0), (0, 0), (P, P), (P, P)), 'constant', constant_values=0)

    # Initialization outputs
    dx = np.zeros(x_pad.shape)
    dw = np.zeros(w.shape)
    db = np.zeros(b.shape)

    # Calculate dx, with 2 extra col/row that will be deleted
    for n in range(N):  # For each element on batch
        for depth in range(F):  # For each filter
            for r in range(0, H, S):    # Slide vertically taking stride into account
                for c in range(0, W, S):    # Slide horizontally taking stride into account
                    dx[n, :, r: r+HH, c: c+WW] += dout[n, depth, r/S, c/S] * w[depth, :, :, :]

    # Calculate db, 1 scalar bias per filter .so it's just a matter of summing
    # all elements of dout per filter
    for depth in range(F):
        db[depth] = np.sum(dout[:, depth, :, :])

    return dx, dw, db

5、卷积运算转换为矩阵运算

使用矩阵运算，能够使得运算速度更快，但也会消耗更多的内存。

5.1 Im2col

前面的代码，使用的是for循环来实现卷积，运算速度不够快，在本节中，我们将学习如何使用矩阵运算来实现卷积，首先，卷积是内核过滤器和它移动之后在图像上选择的区域之间的点积，如果我们在内存上扩展所有可能的窗口并将点积作为矩阵运算，运算速度将更快，但内存的消耗也会更大。

例如，输入图片为227*227*3，卷积核为11*11*3，步长为4，padding为0，进行卷积运算的时候，我们可以将卷积核在输入图片上采样的11*11*3大小的像素块（感受野）拉伸为大小为11*11*3=363的列向量，227*227*3大小的图片，又有步长为4，padding为0，卷积之后的宽高计算方式为（227-11）/4）+1=55，所以采样之后得到55*55个11*11*3大小的像素块（感受野），最终可以得到尺寸为363*3025的输出矩阵X_col，（3025由55*55得到，表示有3025个感受野）

总结一下，如何计算im2col输出的大小：

[img_height, img_width, img_channels] = size(img);
newImgHeight = floor(((img_height + 2*P - ksize) / S)+1);
newImgWidth = floor(((img_width + 2*P - ksize) / S)+1);
cols = single(zeros((img_channels*ksize*ksize),(newImgHeight * newImgWidth)));
卷积核也进行类似的伸展，假设有96个大小为11*11*3的卷积核，通过im2col函数之后，得到96*363的矩阵W_col.

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

将图像和卷积核转换之后，卷积操作就变成了简单的矩阵乘法运算，这个例子中，W_col(96*363)c乘以X_col(363*3025)得到的矩阵是96*3025，最后可以重塑为55*55*96，重塑可以定义一个col2im的函数来实现。

5.2前向传播计算图

下图是前向传播中使用im2col之后的计算图，输入为4*4*3，步长为1，padding为0，卷积核大小为2*2，卷积核个数为1：

前向传播代码如下：

def conv_forward_naive(x, w, b, conv_param):
  """
  A naive implementation of the forward pass for a convolutional layer.
  The input consists of N data points, each with C channels, height H and width
  W. We convolve each input with F different filters, where each filter spans
  all C channels and has height HH and width HH.
  Input:
  - x: Input data of shape (N, C, H, W)
  - w: Filter weights of shape (F, C, HH, WW)
  - b: Biases, of shape (F,)
  - conv_param: A dictionary with the following keys:
    - 'stride': The number of pixels between adjacent receptive fields in the
      horizontal and vertical directions.
    - 'pad': The number of pixels that will be used to zero-pad the input.
  Returns a tuple of:
  - out: Output data, of shape (N, F, H', W') where H' and W' are given by
    H' = 1 + (H + 2 * pad - HH) / stride
    W' = 1 + (W + 2 * pad - WW) / stride
  - cache: (x, w, b, conv_param)
  """
  out = None
  pad_num = conv_param['pad']
  stride = conv_param['stride']
  N,C,H,W = x.shape
  F,C,HH,WW = w.shape
  H_prime = (H+2*pad_num-HH) // stride + 1
  W_prime = (W+2*pad_num-WW) // stride + 1
  out = np.zeros([N,F,H_prime,W_prime])
  #im2col
  for im_num in range(N):
      im = x[im_num,:,:,:]
      im_pad = np.pad(im,((0,0),(pad_num,pad_num),(pad_num,pad_num)),'constant')
      im_col = im2col(im_pad,HH,WW,stride)
      filter_col = np.reshape(w,(F,-1))
      mul = im_col.dot(filter_col.T) + b
      out[im_num,:,:,:] = col2im(mul,H_prime,W_prime,1)
  cache = (x, w, b, conv_param)
  return out, cache

im2col函数：

def im2col(x,hh,ww,stride):
    """
    Args:
      x: image matrix to be translated into columns, (C,H,W)
      hh: filter height
      ww: filter width
      stride: stride
    Returns:
      col: (new_h*new_w,hh*ww*C) matrix, each column is a cube that will convolve with a filter
            new_h = (H-hh) // stride + 1, new_w = (W-ww) // stride + 1
    """
    c,h,w = x.shape
    new_h = (h-hh) // stride + 1
    new_w = (w-ww) // stride + 1
    col = np.zeros([new_h*new_w,c*hh*ww])
    for i in range(new_h):
       for j in range(new_w):
           patch = x[...,i*stride:i*stride+hh,j*stride:j*stride+ww]
           col[i*new_w+j,:] = np.reshape(patch,-1)
    return col

5.3反向传播图

使用im2col，计算图类似于具有相同格式的FC层：

$$f(x,\theta,\beta) = (x. \theta^{T}) + \beta$$
，不同之处在于有一堆重塑，转置和im2col块。

关于在反向传播期间的重塑和转置，只需要再次使用另一个重塑或转置来反转它们的操作，需要注意的是，如果在向前传播期间使用行优先进行重塑，反向传播中也要使用行优先。

im2col反向传播操作时。无法实现简单的重塑。这是因为感受野实际上是重合的（取决于步长），所以需要将感受野相交的地方的梯度相加。

反向传播代码：

def conv_backward_naive(dout, cache):
  """
  A naive implementation of the backward pass for a convolutional layer.
  Inputs:
  - dout: Upstream derivatives.
  - cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive
  Returns a tuple of:
  - dx: Gradient with respect to x
  - dw: Gradient with respect to w
  - db: Gradient with respect to b
  """
  dx, dw, db = None, None, None
  x, w, b, conv_param = cache
  pad_num = conv_param['pad']
  stride = conv_param['stride']
  N,C,H,W = x.shape
  F,C,HH,WW = w.shape
  H_prime = (H+2*pad_num-HH) // stride + 1
  W_prime = (W+2*pad_num-WW) // stride + 1
  dw = np.zeros(w.shape)
  dx = np.zeros(x.shape)
  db = np.zeros(b.shape)
  # We could calculate the bias by just summing over the right dimensions
  # Bias gradient (Sum on dout dimensions (batch, rows, cols)
  #db = np.sum(dout, axis=(0, 2, 3))
  for i in range(N):
      im = x[i,:,:,:]
      im_pad = np.pad(im,((0,0),(pad_num,pad_num),(pad_num,pad_num)),'constant')
      im_col = im2col(im_pad,HH,WW,stride)
      filter_col = np.reshape(w,(F,-1)).T
      dout_i = dout[i,:,:,:]
      dbias_sum = np.reshape(dout_i,(F,-1))
      dbias_sum = dbias_sum.T
      #bias_sum = mul + b
      db += np.sum(dbias_sum,axis=0)
      dmul = dbias_sum
      #mul = im_col * filter_col
      dfilter_col = (im_col.T).dot(dmul)
      dim_col = dmul.dot(filter_col.T)
      dx_padded = col2im_back(dim_col,H_prime,W_prime,stride,HH,WW,C)
      dx[i,:,:,:] = dx_padded[:,pad_num:H+pad_num,pad_num:W+pad_num]
      dw += np.reshape(dfilter_col.T,(F,C,HH,WW))
  return dx, dw, db

col2im函数：

def col2im(mul,h_prime,w_prime,C):
    """
      Args:
      mul: (h_prime*w_prime*w,F) matrix, each col should be reshaped to C*h_prime*w_prime when C>0, or h_prime*w_prime when C = 0
      h_prime: reshaped filter height
      w_prime: reshaped filter width
      C: reshaped filter channel, if 0, reshape the filter to 2D, Otherwise reshape it to 3D
    Returns:
      if C == 0: (F,h_prime,w_prime) matrix
      Otherwise: (F,C,h_prime,w_prime) matrix
    """
    F = mul.shape[1]
    if(C == 1):
        out = np.zeros([F,h_prime,w_prime])
        for i in range(F):
            col = mul[:,i]
            out[i,:,:] = np.reshape(col,(h_prime,w_prime))
    else:
        out = np.zeros([F,C,h_prime,w_prime])
        for i in range(F):
            col = mul[:,i]
            out[i,:,:] = np.reshape(col,(C,h_prime,w_prime))
    return out

col2im_back函数：

def col2im_back(dim_col,h_prime,w_prime,stride,hh,ww,c):
    """
    Args:
      dim_col: gradients for im_col,(h_prime*w_prime,hh*ww*c)
      h_prime,w_prime: height and width for the feature map
      strid: stride
      hh,ww,c: size of the filters
    Returns:
      dx: Gradients for x, (C,H,W)
    """
    H = (h_prime - 1) * stride + hh
    W = (w_prime - 1) * stride + ww
    dx = np.zeros([c,H,W])
    for i in range(h_prime*w_prime):
        row = dim_col[i,:]
        h_start = (i / w_prime) * stride
        w_start = (i % w_prime) * stride
        dx[:,h_start:h_start+hh,w_start:w_start+ww] += np.reshape(row,(c,hh,ww))
    return dx

5.4小案例

这里使用X[3x3]与W [2x2]进行卷积的简单示例，来帮助大家的理解。

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

池化层

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$
池化层用于减少特征空间的维度，但是不会改变特征图的深度，它的左右有如下的几点：

1. 减少了特征空间信息，内存的使用更少，计算速度也将快
2. 防止过拟合
3. 引入了位移不变性，更关注是否存在某些特征而不是特征具体的位置。比如最常见的max pooling，因为取一片区域的最大值，所以这个最大值在该区域内无论在哪，max-pooling之后都是它，相当于对微小位移的不变性。

使用的最多的是最大池化，如下图所示，最大池化像卷积核一样滑动窗，并在窗口上获得最大值作为输出。

参数有：
1. 输入：H1 x W1 x Depth_In x N.
2. 步长：控制窗口滑动的像素数量的标量。
3. K：内核大小
4. 输出：H2 x W2 x Depth_Out x N:

$$W_2 = (W_1 - K)/S + 1 \\ H_2 = (H_1 - K)/S + 1 \\ Depth_{out} = Depth_{in}$$

由于池化层上没有可学习的参数，所以它的反向传播更简单。

最大池在其计算图上使用一系列最大节点。因此，最大池化层的反向传播包含在前向传播期间选择的所有元素和dout的掩码之间的乘积。
换句话说，最大池层的输入的梯度是由前向传播选择的元素的梯度和0组成的张量。
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

1、python实现池化层的前向传播

池化层上的窗口移动机制与卷积核相同，不同之处在于池化层的窗口是选择最大值。

import numpy as np
def max_pool_forward_naive(x, pool_param):
    """
    Compute the forward max pooling (naive way)
    :param x: 4d Input tensor, of shape (N, C, H, W)
    :param pool_param: dictionary with the following keys:
                - 'pool_heigh/width': Sliding window height/width
                - 'stride': Sliding moving distance
    N: Mini-batch size
    C: Input depth (ie 3 for RGB images)
    H/W: Image height/width

    :returns: a tuple of (out, cache)
    """
    # Get input tensor and parameter data
    N, C, H, W = x.shape
    S = pool_param['stride']
    # Consider H_P and W_P as the sliding window height and width
    H_P = pool_param['pool_height']
    W_P = pool_param['pool_height']

    # Calculate output size
    out = None
    HH = 1 + (H - H_P) / S
    WW = 1 + (W - W_P) / S
    out = np.zeros((N, C, HH, WW))

    # Calculate output
    for n in range(N):  # For each element on batch
        for depth in range(C):  # For each input depth
            for r in range(0, H, S):  # Slide vertically taking stride into account
                for c in range(0, W, S):  # Slide horizontally taking stride into account
                    out[n, depth, r/S, c/S] += np.max(x[n, depth, r: r+H_P, c: c+W_P])

    # Return output and save inputs and parameters to cache
    cache = (x, pool_param)
    return out, cache

2、python实现池化层的反向传播

def max_pool_backward_naive(dout, cache):
    """
    Compute the backward propagation of max pooling (naive way)
    :param dout: Upstream derivatives(衍生物), same size as cached x
    :param cache: A tuple of (x, pool_param) as in the forward pass.
    :returns:
    - dx: Gradient with respect to x
    """
    # Get data back from cache
    x, pool_param = cache

    # Get input tensor and parameter
    N, C, H, W = x.shape
    S = pool_param['stride']
    # Consider H_P and W_P as the sliding window height and width
    H_P = pool_param['pool_height']
    W_P = pool_param['pool_height']
    N, C, HH, WW = dout.shape

    # Initialize dx
    dx = None
    dx = np.zeros(x.shape)

    # Calculate dx (mask * dout)
    for n in range(N):  # For each element on batch
        for depth in range(C):  # For each input depth
            for r in range(HH):  # Slide vertically taking stride on the fly
                for c in range(WW):  # Slide horizontally taking stride on the fly
                    # Get window and calculate the mask
                    x_pool = x[n, depth, r * S: r * S + H_P, c * S: c * S + W_P]
                    mask = (x_pool == np.max(x_pool))
                    # Calculate mask * dout
                    dx[n, depth, r*S: r*S+H_P, c*S: c*S+W_P] = mask*dout[n, depth, r, c]

    # Return dx
    return dx