谱聚类的增量更新原理

最新推荐文章于 2022-07-27 15:43:59 发布

morris_mao

最新推荐文章于 2022-07-27 15:43:59 发布

阅读量2k

点赞数

分类专栏：机器学习文章标签：谱聚类复杂网络机器学习

本文链接：https://blog.csdn.net/u010754290/article/details/48199139

版权

机器学习专栏收录该内容

2 篇文章 0 订阅

订阅专栏

一、导言

谱聚类（Spectral Clustering）因为其严谨的理论基础及其能够处理复杂聚类形状的优势，在实践中存在大规模的应用。

对谱聚类有一定了解的同学一定知道，谱聚类有两种解释的观点：图分割和随机游走，Laplacian矩阵的特征值分解如何等价（近似）与图分割或随机游走的数学证明不在本篇博客的范围内。

当我们被给定一个dataset，不管我们用哪一种方式去求解Laplacian矩阵的特征值和特征向量，最终得到的是该dataset内所有样本点所属的cluster。这就引入了该篇博客想要阐述的问题：

当我们更新dataset中的样本点或向dataset中增加样本点，是否存在某种（近似）方法能够在低时间复杂度上动态更新特征值和特征向量，能够避免每次重新求解。

本博客主要参考论文“Incremental spectral clustering by efficiently updating the eigen-system”，以下即对该论文的核心观点进行深度解读。

二、算法原理

1、先导

该篇博客内涉及到非常多谱聚类的背景知识，这些前导知识对理解谱聚类的增量更新方式非常重要，建议读者优先阅读Von Luxburg的”A tutorial on spectral clustering”，见文献[1]。

博客中的算法原理、公式推导主要参考文献[2]，爱智求真的读者可以直接阅读原文文献。

另外，该博客以算法展示和可行性论证为主；而公式推导部分非常繁杂，有时间我会在以后的博客中深究推导。

2、问题引入

当我们对下图中的a进行谱聚类（聚类数量=2）的时候，我们发现 $ABC$ 和 $DEF$ 能够成为两个聚类。但当我们调整 $Edge_{CD}=0.1$ 至 $Edge_{CD}=0.5$ 、同时增加 $Edge_{FG} = 0.5$ 的时候，通过谱聚类发现 $ABCD$ 和 $EFG$ 成为两个聚类。

这里写图片描述

当“边的增删改”动作非常频繁，且我们要处理的图非常大的时候，每次全图进行谱聚类的开销会无法承担。

那么接下来论文中提出了一种很实用的算法框架，能够在近似O(n)的时间复杂度上对谱聚类得到的特征值和特征向量进行更新。

3、Incidence vector & Incidence matrix

incidence vector的定义如下：

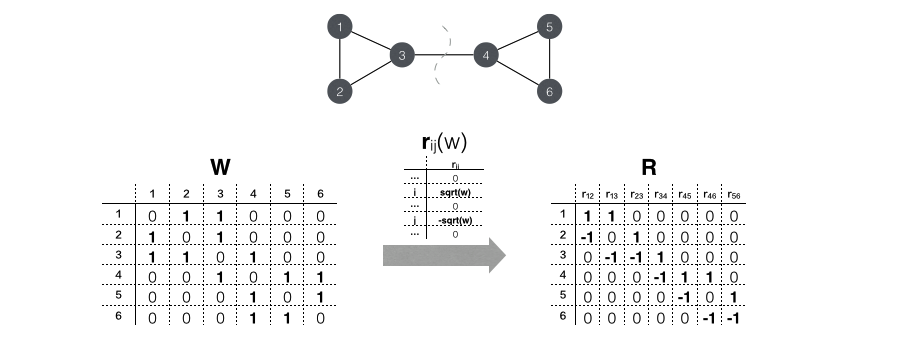
Incidence vector $\mathbf{r}_{ij}(w)$ 是一个列向量（长度为样本点的数量），第 $i$ 个位置上的值为 $\sqrt{w}$ 、第 $j$ 个位置上的值为 $-\sqrt{w}$ ，其余位置的值为 $0$ 。

incidence matrix的定义如下：

Incidence matrix $R$ 的每一列为一个incidence vector。

由定义我们可以发现，incidence matrix $R$ 内包含了相似度矩阵的所有信息。下面我们用一个6个节点的网络进行示意：

这里写图片描述

那么接下来我们可以得到这样的结论：

$L = R R^T$ ，其中 $R = {\mathbf{r}_{ij}(w_{ij}): 1 \leq i < j \leq n }$

（此处证明略去，读者可自行证明。）

那么对于上述6节点的网络示例，我可以做出以下推断：

$R R T = = = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ 1 - 1 0000 10 - 1 000 01 - 1 000 001 - 1 00 0001 - 1 0 0001 - 1 - 1 00001 - 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ * ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ 1100000 - 1 010000 0 - 1 - 1 1000 000 - 1 110 0000 - 1 01 00000 - 1 - 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ 2 - 1 - 1 000 - 1 2 - 1 000 - 1 - 1 3 - 1 00 00 - 1 3 - 1 - 1 000 - 1 2 - 1 000 - 1 - 1 2 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ L$ $\begin{align} R R^T =& \begin{bmatrix} 1 & 1 & 0 & 0 & 0 & 0 & 0\\ -1& 0 & 1 & 0 & 0 & 0 & 0\\ 0 & -1 & -1 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -1 & 1 &1 & 0\\ 0 & 0 & 0 & 0 & -1 &-1 & 1\\ 0 & 0 & 0 & 0 & 0 &-1 & -1\\ \end{bmatrix} * \begin{bmatrix} 1&-1&0&0&0&0\\ 1&0&-1&0&0&0\\ 0&1&-1&0&0&0\\ 0&0&1&-1&0&0\\ 0&0&0&1&-1&0\\ 0&0&0&1&0&-1\\ 0&0&0&0&1&-1\\ \end{bmatrix}\\ =& \begin{bmatrix} 2&-1&-1&0&0&0\\ -1&2&-1&0&0&0\\ -1&-1&3&-1&0&0\\ 0&0&-1&3&-1&-1\\ 0&0&0&-1&2&-1\\ 0&0&0&-1&-1&2\\ \end{bmatrix}\\ =&L \end{align}$

接下去，如果样本点 $i$ 和 $j$ 有了一次相似度的改变 $\Delta w_{ij}$ ，那么对应的incident vector可以表达为 $\mathbf{r}_{ij}(\Delta w_{ij})$ 。新的Laplacian矩阵可以表达为 $\tilde{L} = \tilde{R} \tilde{R}^T$ ，其中 $\tilde{R} = [R, \mathbf{r}_{ij}(\Delta w_{ij})]$ 。

这样我们可以引出：

$Δ L = L ̃ - L = Δ w i j u i j u T i j Δ D = Δ w i j d i a g {v i j}$ $\Delta L = \tilde{L} - L = \Delta w_{ij} \mathbf{u}_{ij} \mathbf{u}_{ij}^T\\ \Delta D = \Delta w_{ij} diag\{\mathbf{v}_{ij}\}$
$\mathbf{u}_{ij}$ 是列向量且第i位置上的值为1，第j位置上未-1，其余为0。
$\mathbf{v}_{ij}$ 是列向量且第i,j位置上的值为1，其余为0。

这样当我们尝试去修改这个图的时候，“边的增删改”操作可以分解为一系列相似度的改变 $\Delta w_{ij}$ 。

4、从Ncut来看谱聚类

根据拉普拉斯矩阵的定义： $L=D-W$ ，我们可以求解 $L$ 的特征值。

$f T L f = = = f T D f - f T W f \sum i = 1 n d i f 2 i - \sum i, j n f i f j w i j 1 2 \sum i, j n w i j (f i - f j) 2$ $\begin{aligned} f^{T}Lf =& f^{T}Df - f^{T}Wf\\ =& \sum_{i=1}^nd_if_i^2 - \sum_{i,j}^nf_if_jw_{ij}\\ =& \frac{1}{2} \sum_{i,j}^n w_{ij}(f_i - f_j)^2 \end{aligned}$

接下去，我们用二分类问题来证明Ncut和求解 $L$ 的特征向量等价：

首先将特征向量的选择条件放宽，假定 $f_i$ 为非正即负：

$f i = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ v o l ( A ¯ ) v o l ( A ) ‾ ‾ ‾ ‾ ‾ \sqrt - v o l ( A ) v o l ( A ¯ ) ‾ ‾ ‾ ‾ ‾ \sqrt i f v i \in A i f v i \in A ¯$ $f_i= \begin{cases} \sqrt{\frac{vol(\bar{A})}{vol(A)}}& if v_i \in A\\ -\sqrt{\frac{vol(A)}{vol(\bar{A})}}& if v_i \in \bar{A} \end{cases}$

那么我们可以证明Ncut等价与normalized谱聚类：

$f T L f = = = = = = 1 2 \sum i, j n w i j (f i - f j) 2 1 2 \sum i \in A, j \in A ¯ w i j ⎛ ⎝ ⎜ ⎜ ∣ ∣ A ¯ ∣ ∣ | A | ‾ ‾ ‾ ‾ \sqrt + | A | ∣ ∣ A ¯ ∣ ∣ ‾ ‾ ‾ ‾ \sqrt ⎞ ⎠ ⎟ ⎟ 2 + 1 2 \sum i \in A ¯, j \in A w i j ⎛ ⎝ ⎜ ⎜ - | A | ∣ ∣ A ¯ ∣ ∣ - ∣ ∣ A ¯ ∣ ∣ | A | ‾ ‾ ‾ ‾ \sqrt ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾ ‾  ⎷   ⎞ ⎠ ⎟ ⎟ 2 ⎛ ⎝ ⎜ ⎜ 1 2 \sum i \in A, j \in A ¯ w i j + 1 2 \sum i \in A ¯, j \in A w i j ⎞ ⎠ ⎟ ⎟ * (| A | ∣ ∣ A ¯ ∣ ∣ + ∣ ∣ A ¯ ∣ ∣ | A | + 2) ⎛ ⎝ ⎜ ⎜ \sum i \in A, j \in A ¯ w i j ⎞ ⎠ ⎟ ⎟ * (v o l ( V ) ∣ ∣ v o l ( A ) ∣ ∣ + v o l ( V ) ∣ ∣ v o l ( A ¯ ) ∣ ∣) v o l (V) * 1 2 \sum i = 1 2 W ( A i , A ¯ i ) v o l ( A i ) v o l (V) * N c u t (A, A ¯)$ $\begin{aligned} f^{T}Lf =& \frac{1}{2} \sum_{i,j}^n w_{ij}(f_i - f_j)^2\\ =& \frac{1}{2} \sum_{i \in A,j \in \bar{A}} w_{ij} \left( \sqrt{\frac{\left| \bar{A} \right|}{\left| A \right|}} + \sqrt{\frac{\left| A \right|}{\left| \bar{A} \right|}} \right)^2 + \frac{1}{2} \sum_{i \in \bar{A},j \in A} w_{ij} \left(- \sqrt{\frac{\left| A \right|}{\left| \bar{A} \right|} -\sqrt{\frac{\left| \bar{A} \right|}{\left| A \right|}} } \right)^2\\ =& \left( \frac{1}{2} \sum_{i \in A,j \in \bar{A}} w_{ij} + \frac{1}{2} \sum_{i \in \bar{A},j \in A} w_{ij} \right) * \left( \frac{\left| A \right|}{\left| \bar{A} \right|} + \frac{\left| \bar{A} \right|}{\left| A \right|} + 2 \right)\\ =& \left( \sum_{i \in A,j \in \bar{A}} w_{ij} \right) * \left( \frac{vol(V)}{\left| vol(A) \right|} + \frac{vol(V)}{\left| vol(\bar{A}) \right|}\right)\\ =& vol(V) * \frac{1}{2}\sum_{i=1}^{2}\frac{W(A_i, \bar{A}_i)}{vol(A_{i})}\\ =& vol(V) * Ncut(A, \bar{A}) \end{aligned}$

由 $k=2$ 我们可以衍生至 $k$ 为任意值时的场景，在此不再继续推导。

5、特征向量 $\Delta \lambda$ 和特征值 $\Delta f$ 的计算

从第4节中，我们推导出：

$Δ L = L ̃ - L = Δ w i j u i j u T i j Δ D = Δ w i j d i a g {v i j}$ $\Delta L = \tilde{L} - L = \Delta w_{ij} \mathbf{u}_{ij} \mathbf{u}_{ij}^T\\ \Delta D = \Delta w_{ij} diag\{\mathbf{v}_{ij}\}$
$\mathbf{u}_{ij}$ 是列向量且第i位置上的值为1，第j位置上未-1，其余为0。
$\mathbf{v}_{ij}$ 是列向量且第i,j位置上的值为1，其余为0。

又由于广义特征系统 $A \mathbf{x} =\lambda B \mathbf{x}$ ，可以做出以下推导：

$A x Δ A x + A Δ x x T Δ A x + x T A Δ x x T Δ A x = λ B x = Δ λ B x + λ Δ B x + λ B Δ x = x T Δ λ B x + x T λ Δ B x + x T λ B Δ x = Δ λ x T B x + λ x T Δ B x$ $\begin{aligned} A \mathbf{x} &= \lambda B \mathbf{x}\\ \Delta A \mathbf{x} + A \Delta\mathbf{x}&= \Delta\lambda B \mathbf{x} + \lambda \Delta B \mathbf{x} + \lambda B \Delta\mathbf{x}\\ \mathbf{x}^T \Delta A \mathbf{x} + \mathbf{x}^T A \Delta\mathbf{x}&= \mathbf{x}^T \Delta\lambda B \mathbf{x} + \mathbf{x}^T \lambda \Delta B \mathbf{x} + \mathbf{x}^T \lambda B \Delta\mathbf{x}\\ \mathbf{x}^T \Delta A \mathbf{x} &= \Delta\lambda \mathbf{x}^T B \mathbf{x} + \lambda \mathbf{x}^T \Delta B \mathbf{x}\\ \end{aligned}$

之后将 $A$ 替换为 $L$ ， $B$ 替换成 $D$ ， $\mathbf{x}$ 替换成 $f$ ，则可以得到：

$Δ λ = Δ w i j f T ( u i j u T i j - λ d i a g { v i j } ) f f T D f = Δ w i j f T u i j u T i j - Δ w i j λ f T d i a g {v i j} f = Δ w i j ((f i - f j) 2 - λ (f 2 i + f 2 j))$ $\begin{aligned} \Delta \lambda &= \Delta w_{ij} \frac{f^T(\mathbf{u}_{ij} \mathbf{u}_{ij} ^T - \lambda diag\{\mathbf{v}_{ij}\})f}{f^TDf}\\ &= \Delta w_{ij} f^T\mathbf{u}_{ij} \mathbf{u}_{ij} ^T - \Delta w_{ij} \lambda f^T diag\{\mathbf{v}_{ij}\}f\\ &= \Delta w_{ij}((f_i - f_j)^2 - \lambda(f_i^2 + f_j^2)) \end{aligned}$

$Δ f = (K T K) - 1 K T N i j h; 其中 K = L - λ D ， h = (Δ λ D + λ Δ D - Δ L) f$ $\begin{aligned} \Delta f &= (K^T K)^{-1} K_{\mathbf{N}_{ij}}^T \mathbf{h} ; 其中 K = L -\lambda D，\mathbf{h} = (\Delta \lambda D + \lambda \Delta D - \Delta L)f \end{aligned}$

注意， $\Delta \lambda$ 可以很快计算出来，但是 $\Delta f$ 的时间复杂度仍然非常高。这时，我们可以做出以下近似：

对于 $\Delta f$ 中 $K$ 的计算，由于一次 $\Delta w_{ij}$ 只会对局部的聚类结果产生影响；那么对于远离 $i,j$ 的任意点 $k$ ， $\Delta f_{ik}或\Delta f_{jk}$ 均为0。

我们定义 $i,j$ 的所有邻居 $\mathbf{N}_{ij} = \{k | w_{ik} > \tau or w_{ik} > \tau \}$ ，其中 $\tau$ 可以进行大小调整以体现 $i,j$ 的邻居信息。这样我们就可以得到：

$Δ f i j = (K T N i j K N i j) - 1 K T N i j h$ $\Delta f_{ij} = (K_{\mathbf{N}_{ij}}^T K_{\mathbf{N}_{ij}})^{-1} K_{\mathbf{N}_{ij}}^T \mathbf{h}$

6、算法主体

Algorithm 迭代更新 $\Delta \lambda$ 和 $\Delta f$ ：
1. 首先根据一次相似度的变化计算 $\Delta w_{ij}$ ；
2. 设 $\Delta f = 0$ ；
3. 计算 $\Delta \lambda = \Delta w_{ij}((f_i - f_j)^2 - \lambda(f_i^2 + f_j^2))$ ；
4. 计算 $\Delta f_{ij} = (K_{\mathbf{N}_{ij}}^T K_{\mathbf{N}_{ij}})^{-1} K_{\mathbf{N}_{ij}}^T \mathbf{h}$ ；
5. 重复步骤2 和 3直到 $\Delta \lambda$ 和 $\Delta f$ 没有明显变化或达到 $n$ 次迭代上限。

由于算法在经过多次对单个图的计算后，误差会不断累积，我们在每隔一段时间重新全局进行谱聚类的计算即可。

7、时间复杂度

根据公式我们能够看到 $\Delta \lambda$ 的时间复杂度为常数，而 $\Delta f$ 的计算时间复杂度为：

$O (N ¯ 2 n) + O (N ¯ 3) + O (N ¯ n) + O (N ¯ 2)$ $O(\bar{N}^2 n) + O(\bar{N}^3) + O(\bar{N} n) + O(\bar{N}^2)$
其中从左到右，分别对应着 $K_{\mathbf{N}_{ij}}^T K_{\mathbf{N}_{ij}}$ 的计算、求逆计算、 $K_{\mathbf{N}_{ij}}^T \mathbf{h}$ 的计算和最终乘积计算， $\bar{N}$ 即由 $\tau$ 决定的邻居的数量。

该算法的时间复杂度比谱聚类的常规解 $O(n^3)$ ，甚至很多近似解（如Labczos解法的 $O(n^{3/2})$ ）都要要小很多。

三、文献

[1] Von Luxburg U. A tutorial on spectral clustering[J]. Statistics and computing, 2007, 17(4): 395-416.
[2] Ning H, Xu W, Chi Y, et al. Incremental spectral clustering by efficiently updating the eigen-system[J]. Pattern Recognition, 2010, 43(1): 113-127.