导言
在Alex Graves的这篇论文《Supervised Sequence Labelling with Recurrent Neural Networks》中对LSTM进行了综述性的介绍,并对LSTM的Forward Pass和Backward Pass进行了公式推导。
这篇文章将用更简洁的图示和公式一步步对Forward和Backward进行推导,相信读者看完之后能对LSTM有更深入的理解。
如果读者对LSTM的由来和原理存在困惑,推荐DarkScope的这篇博客:《RNN以及LSTM的介绍和公式梳理》
一、LSTM的基础结构
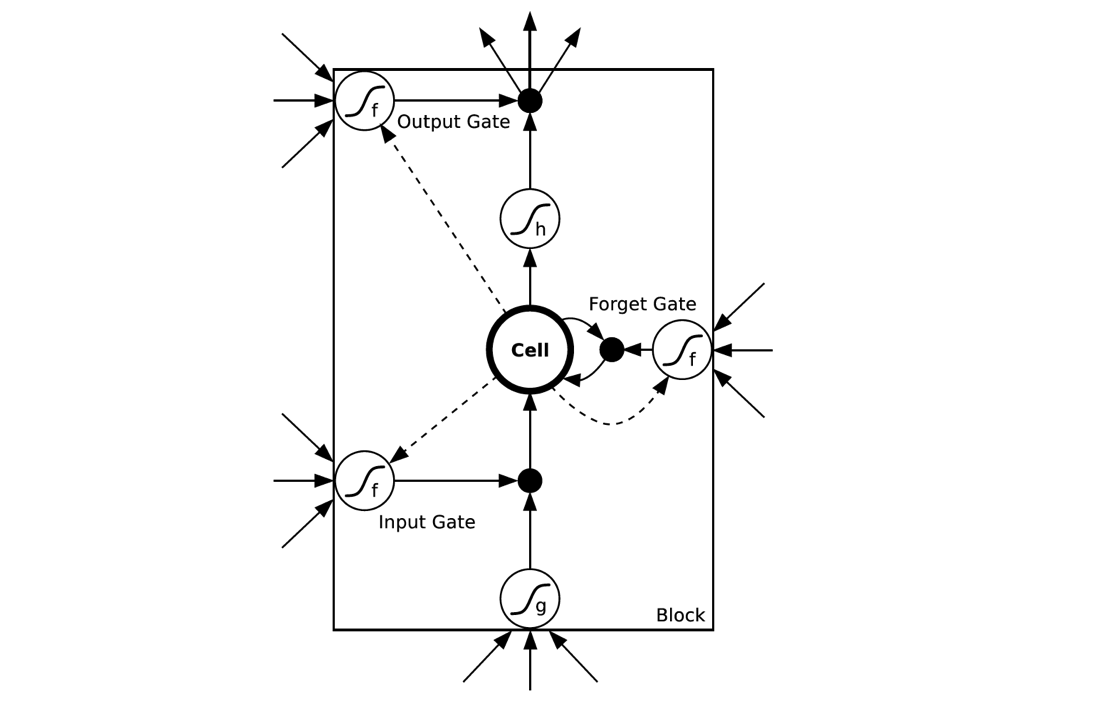
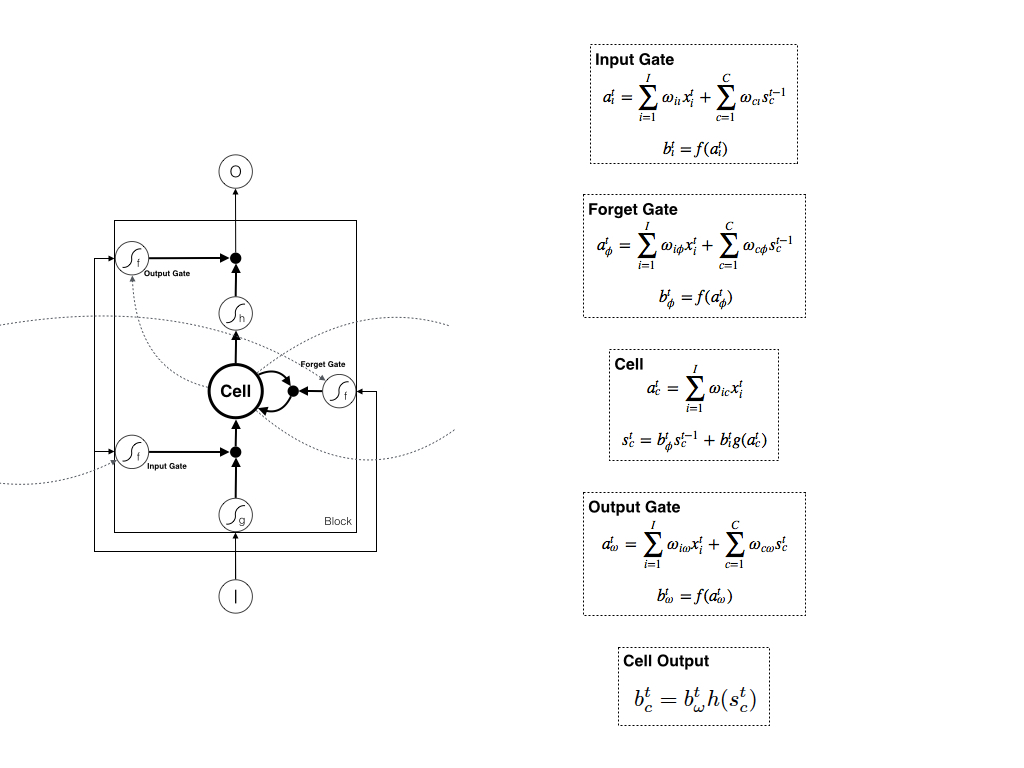
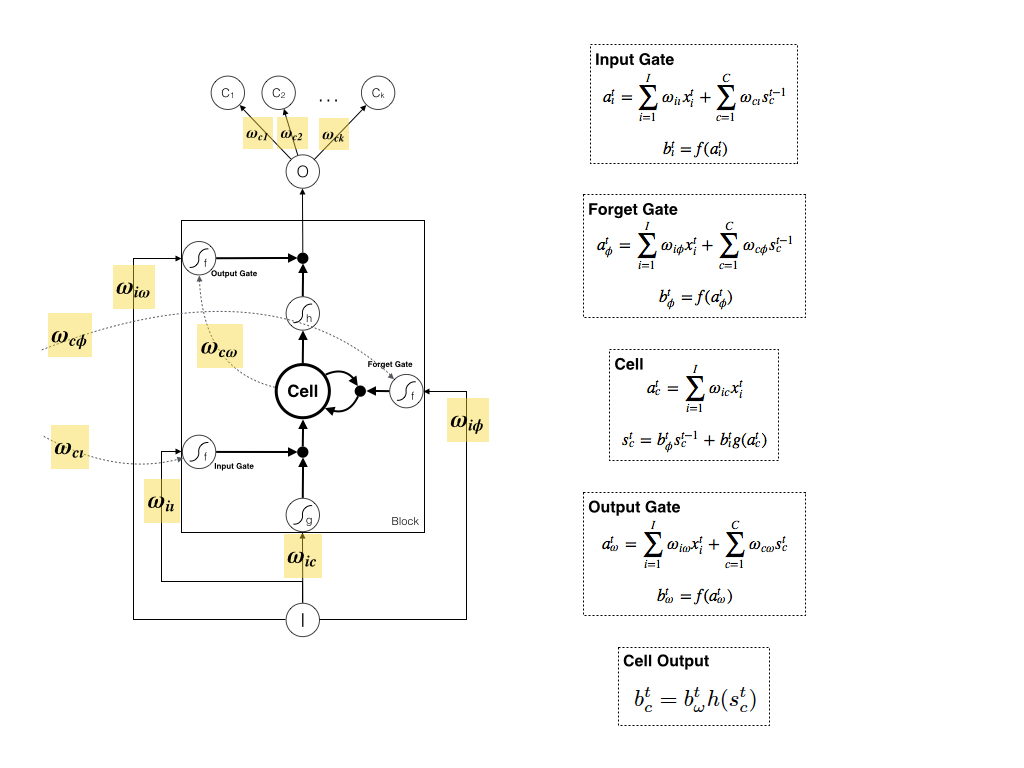
LSTM的结构中每个时刻的隐层包含了多个memory blocks(一般我们采用一个block),每个block包含了多个memory cell,每个memory cell包含一个Cell和三个gate,一个基础的结构示例如下图:
一个memory cell只能产出一个标量值,一个block能产出一个向量。
二、LSTM的前向传播(Forward Pass)
1. 引入
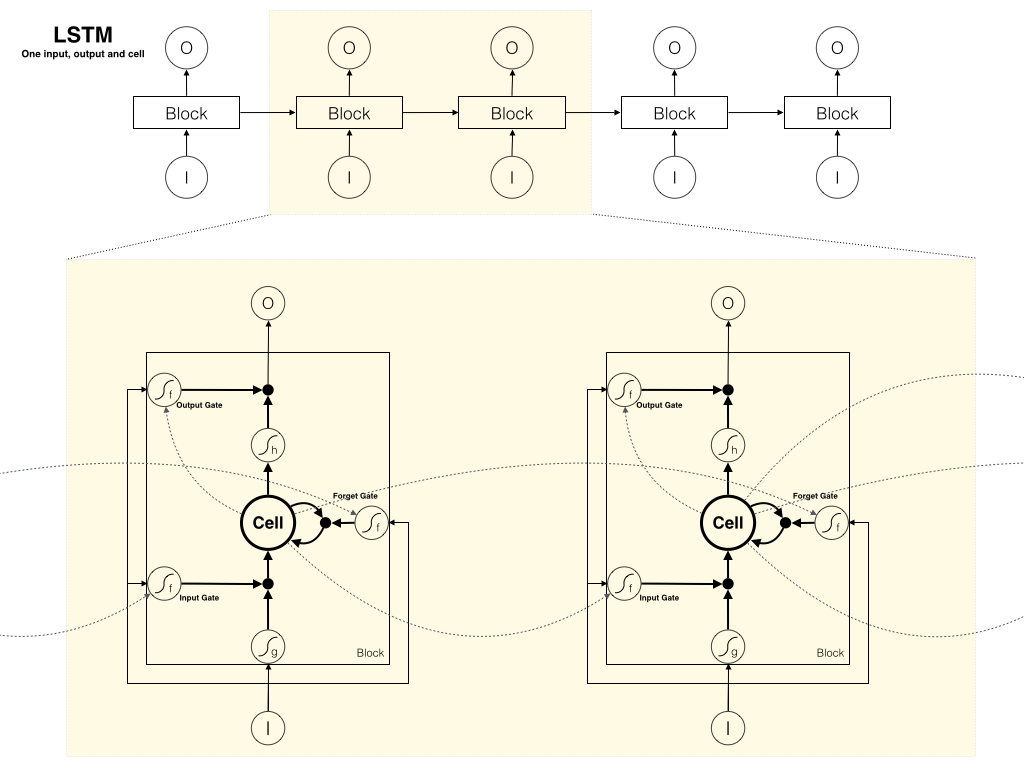
首先我们在上述LSTM的基础结构之上构造时序结构,这样让读者更清晰地看到Recurrent的结构:
这里我们有几个约定:
- 每个时刻的隐层包含一个block
- 每个block包含一个memory cell
下面前向传播我们则从Input开始,逐个求解Input Gate、Forget Gate、Cells Gate、Ouput Gate和最终的Output
这里需要申明的一点,推导过程严格按照上述图示LSTM的结构;论文中对相较于该文章的推导过程会有增加一些项,在每一个公式不一致的地方我都会有相应说明。
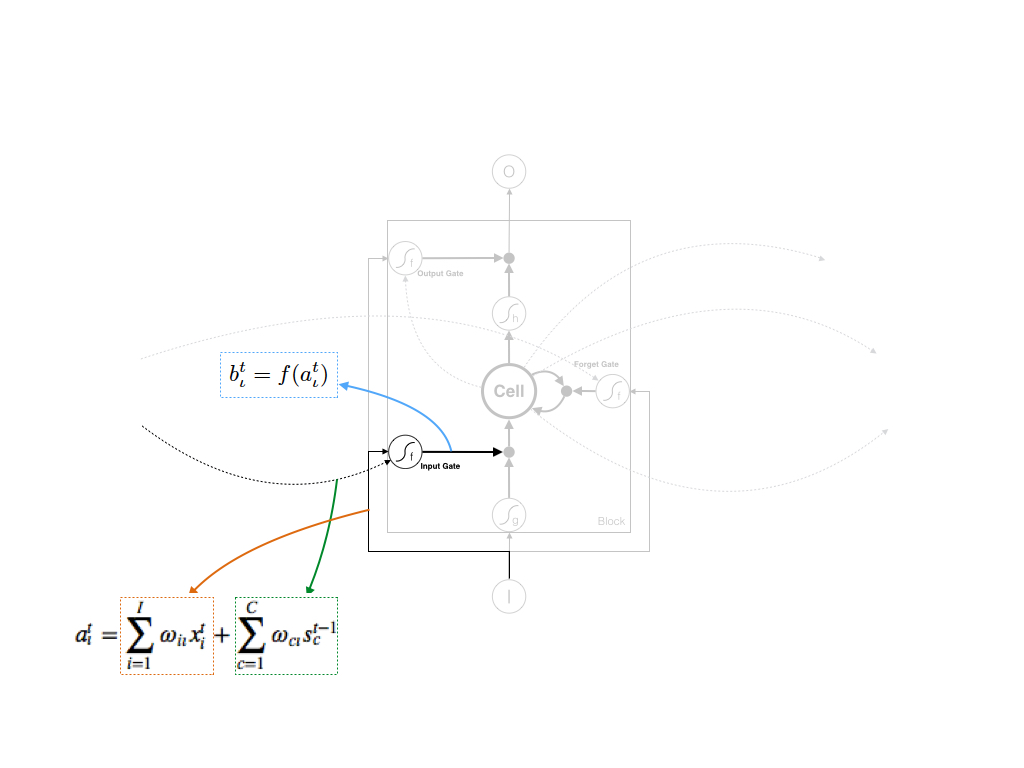
2. Input Gate( ι ) 的计算
Input Gate接受两个输入:
- 当前时刻的Input作为输入: xt
- 上一时刻同一block内所有Cell作为输入: st−1c
该案例中每层仅有单个Block、单个cemory cell,可以忽略 ∑Cc=1 ,以下Forget Gate和Output Gate做相同处理。
最终Input Gate的输出为:
这里Input Gate还可以接受上一个时刻中不同block的输出 bt−1h 作为输入,论文中 atι 会增加一项 ∑Hh=1ωhιbt−1h 。
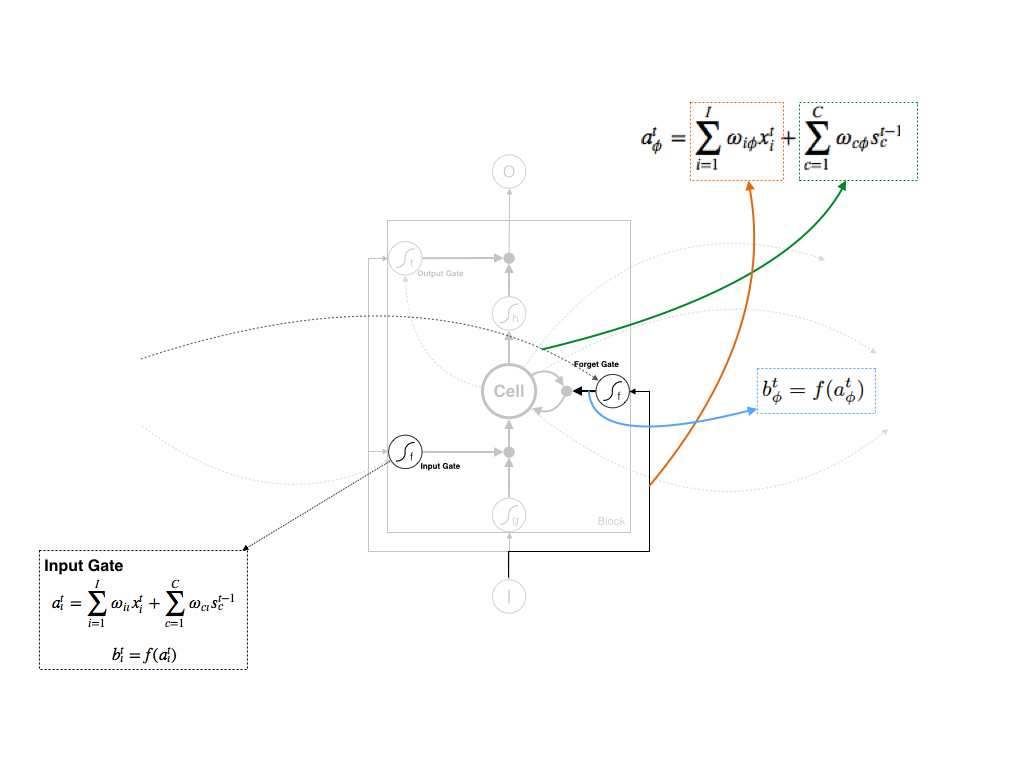
3. Forget Gate( ϕ ) 的计算
Forget Gate接受两个输入:
- 当前时刻的Input作为输入: xt
- 上一时刻同一block内所有Cell作为输入: st−1c
最终Forget Gate的输出为:
这里Input Gate还可以接受上一个时刻中不同block的输出 bt−1h 作为输入,论文中 atϕ 会增加一项 ∑Hh=1ωhϕbt−1h 。
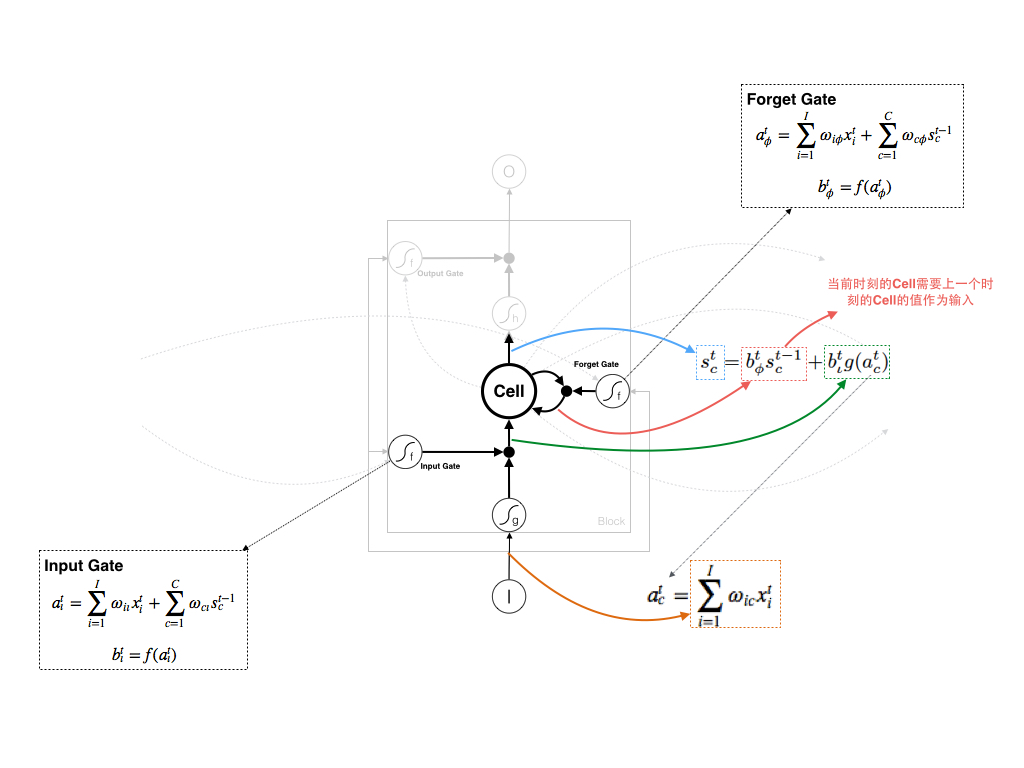
4. Cell( c ) 的计算
Cell的计算稍有些复杂,接受两个输入:
- Input Gate和Input输入的乘积
- Forget Gate和上一时刻对应Cell输出的乘积
最终Cell的输出为:
这里Input Gate还可以接受上一个时刻中不同block的输出 bt−1h 作为输入,论文中 atc 会增加一项 ∑Hh=1ωhcbt−1h 。
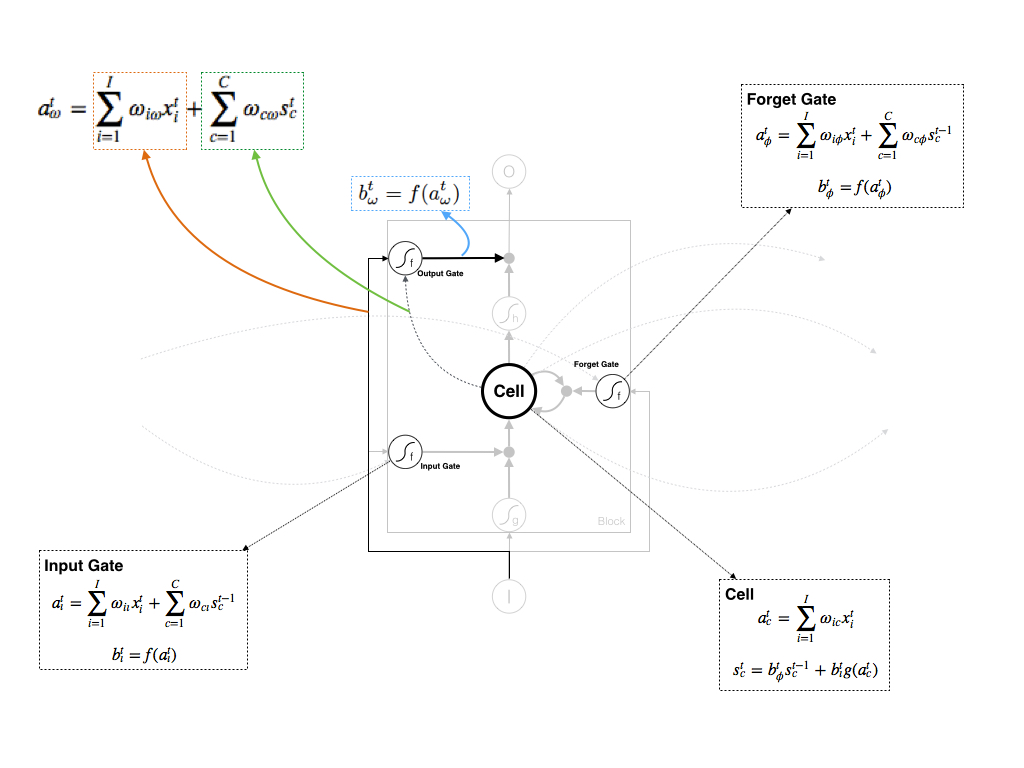
5. Output Gate( ω ) 的计算
Output Gate接受两个输入:
- 当前时刻的Input作为输入: xt
- 当前时刻同一block内所有Cell作为输入: stc
这里Output Gate接受“当前时刻Cell的输出”而不是“上一时刻Cell的输出”,是由于此时Cell的结果已经产出,我们控制Output Gate的输出直接采用Cell当前的结果就行了,无须使用上一时刻。
最终Output Gate的输出为:
这里Cell还可以接受上一个时刻中其他gate链接过来的边,论文中 atϕ 会增加一项 ∑Hh=1ωhϕbt−1h ,这里 H 是泛指t-1时刻的Cell或三个Gate。
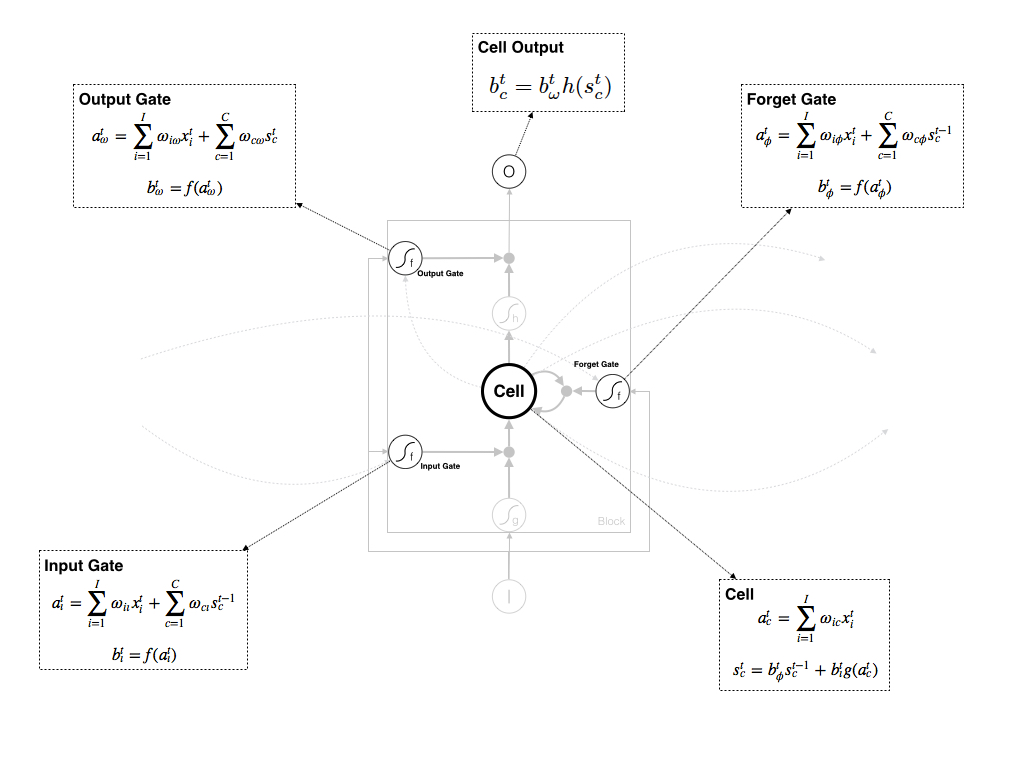
6. Cell Output(c ) 的计算
Cell Output的计算即将Output Gate和Cell做乘积即可。
最终Cell Output为:
7. 小结
至此,整个Block从Input到Output整个Forward Pass已经结束,其中涉及三个Gate和中间Cell的计算,需要注意的是三个Gate使用的激活函数是
f
,而Input的激活函数是
这里读者需要注意,在整个计算过程中,当前时刻的三个Gate均可以从上一时刻的任意Gate中接受输入,在公式中存在体现,但是在图示中并未画出相应的边。我们可以认为只有上一时刻的Cell才和当前时刻的Cell或三个Gate相连。
三、LSTM的反向传播(Backward Pass)
1. 引入
此处在论文中使用“Backward Pass”一词,但其实即Back Propagation过程,利用链式求导求解整个LSTM中每个权重的梯度。
2. 损失函数的选择
为了通用起见,在此我们仅展示多分类问题的损失函数的选择,对于网络的最终输出我们利用
注意, yk 对 ak 的偏导为 ∂yk′∂ak=ykδkk′−ykyk′ ( δkk′ 当 k==k′ 时为1,其他为0)
其中,对于网络输出
a1,a2,...
对应我们可以得到
p(C1|x),p(C2|x),...
,即给定输入
x
输出类别为
这样损失函数(Loss Function)就很好定义了:对于 k∈1,2,...,K ,网络输出的类别为k概率为 yk ,而真实值 zk :
3. 权重的更新
对于神经网络中的每一个权重,我们都需要找到对应的梯度,从而通过不断地用训练样本进行随机梯度下降找到全局最优解,那么首先我们需要知道哪些权重需要更新。
一般层次分明的神经网络有input层、hidden层和output层,层与层之间的权重比较直观;但在LSTM中通过公式才能找到对应的权重,和图示中的边并不是一一对应,下面我将LSTM的单个Block中需要更新的权重在图示上标示了出来:
为了方便起见,这里需要申明的是:我们仅考虑上一时刻的Cell仅和当前时刻的Cell和三个Gate相连。
2. Cell Output的梯度
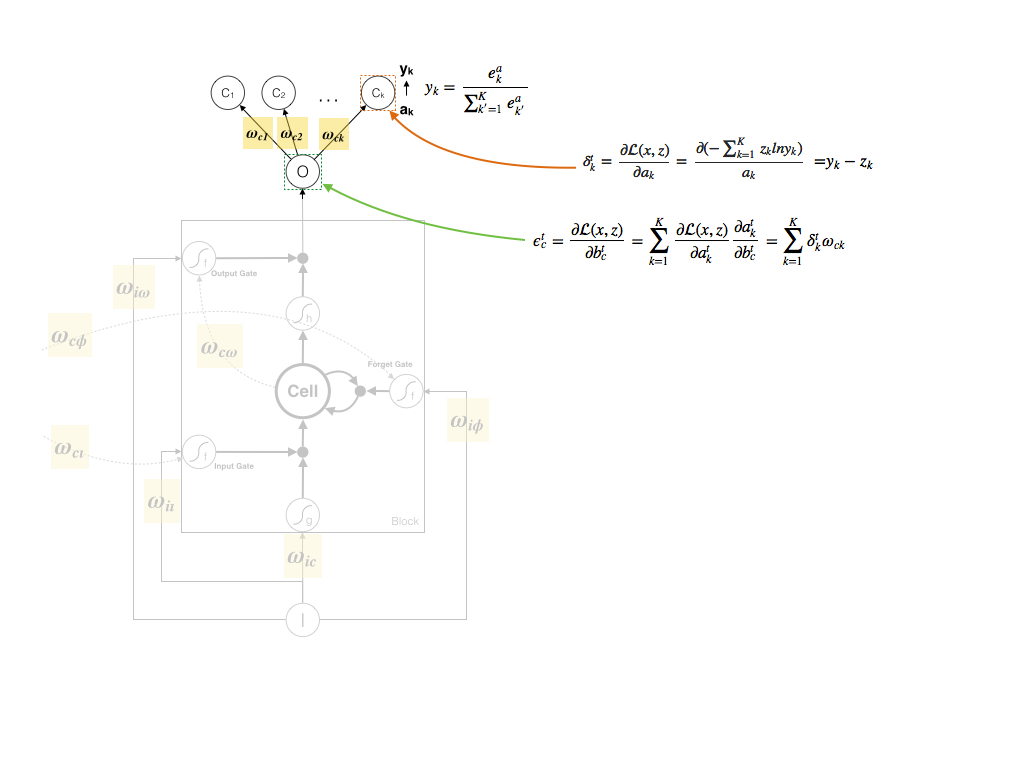
首先我们计算每一个输出类别的梯度:
也即每一个输出类别的梯度仅和其预测值和真实值相关,这样对于Cell Output的梯度则可以通过链式求导法则推导出来:
由于Output还可以连接下一个时刻的一个Cell、三个Gate,那么下一个时刻的一个Cell、三个Gate的梯度则可以传递回当前时刻Output,所以在论文中存在额外项 ∑Gg=1ωcgδt+1g ,为简便起见,公式和图示中未包含。
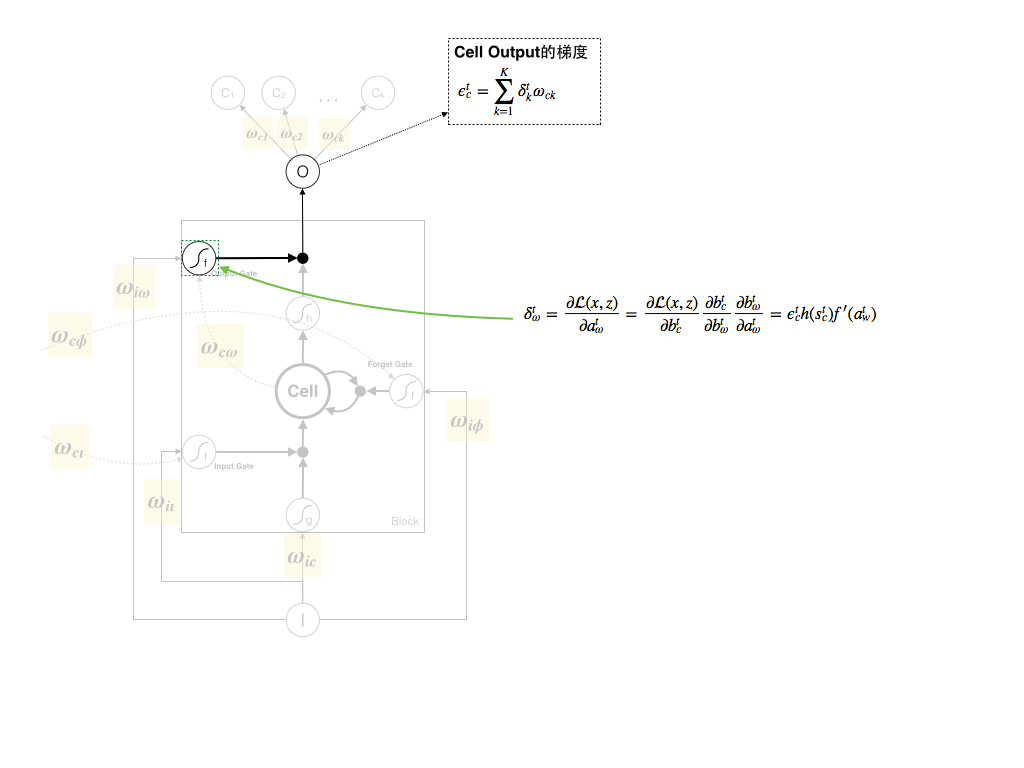
3. Output Gate的梯度
根据链式求导法则,Output Gate的梯度可以由以下公式推导出来:
另外,由于单个Block内可以存在多个memory cell、一个Forget Gate、一个Input Gate和一个Output Gate,论文中将Output Gate的梯度写成了 f′(atw)∑Cc=1ϵtch(stc) ,但推导过程一致。推导过程见下图,说明梯度汇总到单个Gate中:
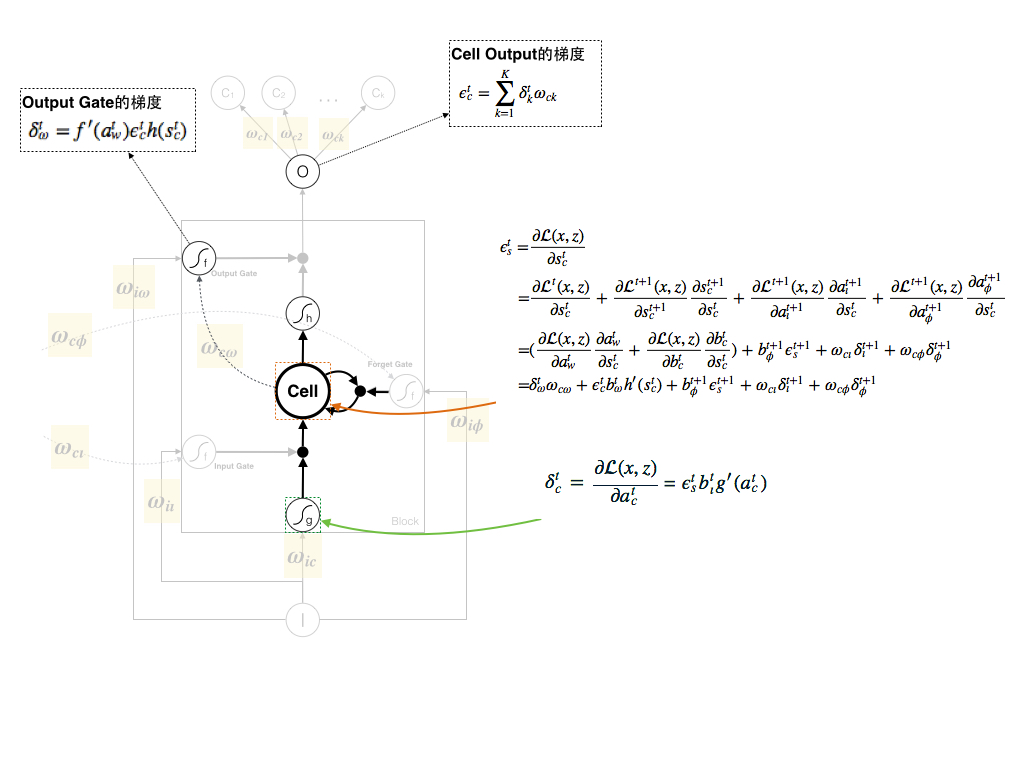
4. Cell的梯度
细心的读者在这里会发现,Cell的计算结构和普遍的神经网络不太一样,让我们首先来回顾一下Cell部分的Forward计算过程:
输入数据贡献给 atc ,而Cell同时能够接受Input Gate和Forget Gate的输入。
这样梯度就直接从Cell向下传递:
在这里,我们定义States,由于Cell的梯度可以由以下几个计算单元传递回来:
- 当前时刻的Cell Output
- 下一个时刻的Cell
- 下一个时刻的Input Gate
- 下一个时刻的Output Gate
那么States可以这样求解,上面1~4个能够回传梯度的计算单元和下面公式中一一对应:
那么:
细心的读者会发现,论文中 ∂(x,z)∂btc 并没有求和,这里作者持保留态度,应该存在求和项。
同时由于Cell可以连接到下一个时刻的Forget Gate、Output Gate和Input Gate,那么下一时刻的这三个Gate则可以将梯度传播回来,所以在论文中我们会发现 ϵts 拥有这三项: bt+1ϕϵt+1s 、 ωclδt+1ι 和 ωcϕδt+1ϕ 。
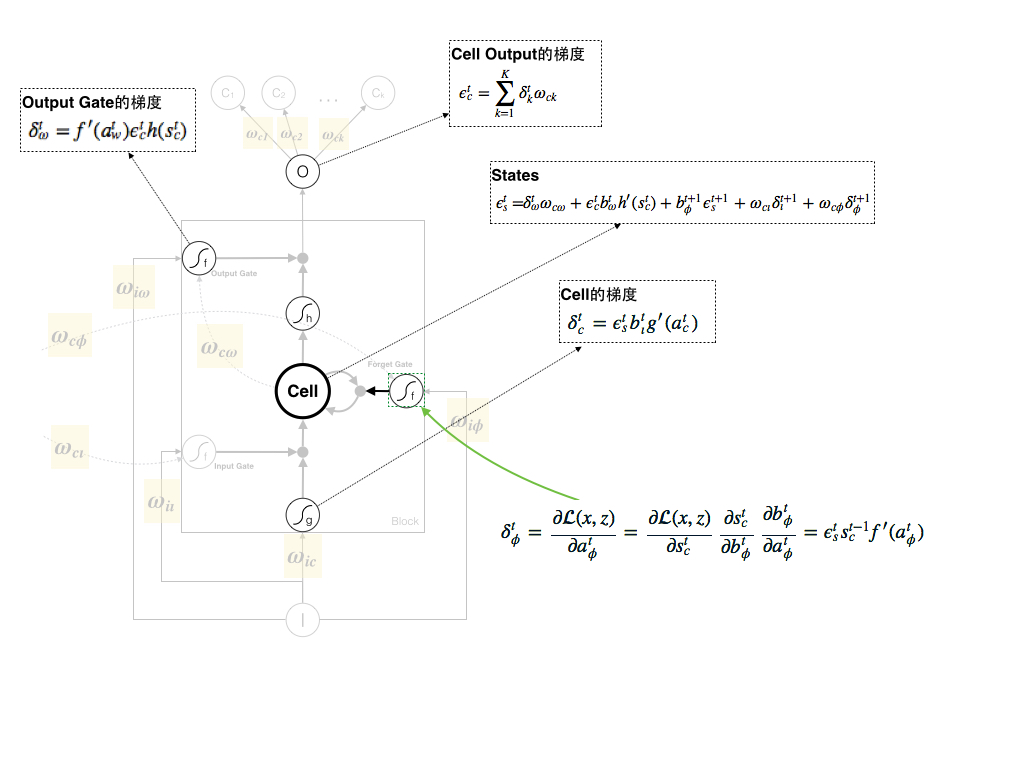
5. Forget Gate的梯度
Forget Gate的梯度计算就比较简单明了:
另外,由于单个Block内可以存在多个memory cell、一个Forget Gate、一个Input Gate和一个Output Gate,论文中将Forget Gate的梯度写成了 f′(atϕ)∑Cc=1st−1cϵts ,但推导过程一致,说明梯度汇总到单个Gate中。
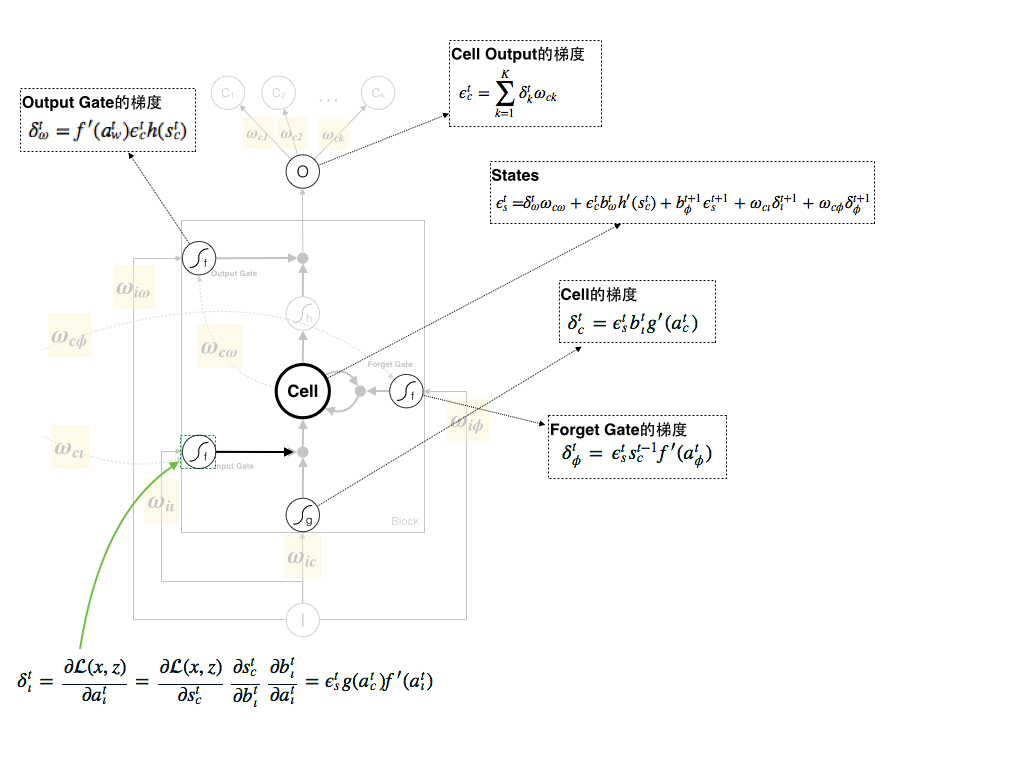
6. Input Gate的梯度
Input Gate的梯度计算如下:
另外,由于单个Block内可以存在多个memory cell、一个Forget Gate、一个Input Gate和一个Output Gate,论文中将Input Gate的梯度写成了 f′(atι)∑Cc=1g(atc)ϵts ,但推导过程一致,说明梯度汇总到单个Gate中。
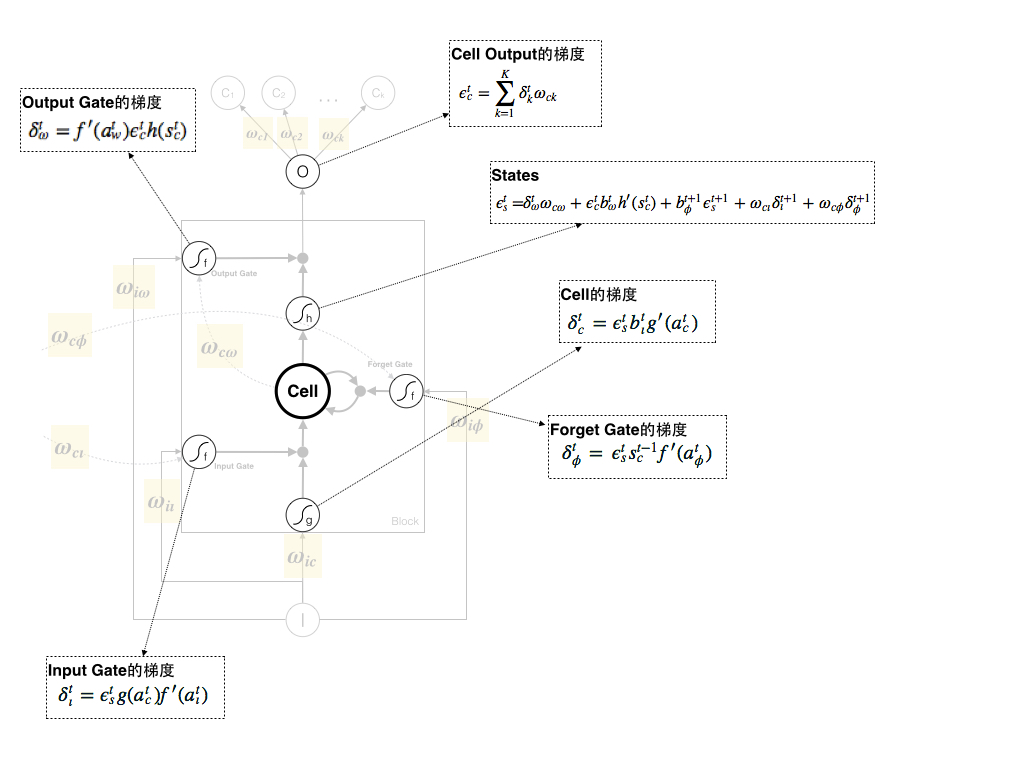
7. 小结
至此,所有的梯度求解已经结束,同样我们将这个Backward Pass的所有公式列出来:
剩下的事情即利用梯度去更新每个权重:
其中 mΔωn−1 为上一次权重的更新值,且 m∈[0,1] ;而 ∂∂ωn 即上面我们求到的每一个梯度。
例如每次更新
ωiϕ
的
Δ
量即:
其中 δtϕ 即Forget Gate的梯度。
三、总结
以上就是LSTM中的前向和反向传播的公式推导,在这里作者仅以最简单的单个Cell的场景进行示例。
在实际工程实践中,常常会涉及到同一时刻多个Cell且互相之间的Gate存在连接,同时上一个时刻或下一个时刻的Cell和三个Gate之间同样存在复杂的连接关系。
但如果读者能够明晰上述的推导过程,那么无论多复杂都能够迎刃而解了。
毛仁歆
2015年7月31日


























 521
521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








