本篇文章主要根据《神经网络与机器学习》和《人工神经网络原理》两本书,对 BP 神经网络的数学推导过程做了一个总结,为自己进入深度学习打下一个基础。
一、 人工神经网络
1.人工神经网络简介
人工神经网络(ANN)是一种旨在模仿人脑结构及其功能的由多个非常简单的处理单元彼此按某种方式相互连接而形成的计算机系统,该系统靠其状态对外部输入信息的动态响应来处理信息 。

神经元由细胞及其发出的许多突起构成。细胞体内有细胞核,突触的作用是传递信息。作为引入输入信号的若干个突起称为“树突”,而作为输出端的突起只有一个称为“轴突” 。
2.神经元M-P模型
所谓M-P模型,其实是按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型。
对于第
j
j
j个神经元,接受多个其它神经元的输入信号
x
i
x_i
xi。各突触强度以实系数
w
i
j
w_{ij}
wij表示,这是第
i
i
i个神经元对第
j
j
j个神经元作用的加权值。

神经元的“净输入”用
I
j
I_j
Ij表示,其表达式是线性加权求和,即:

神经元
j
j
j的输出
y
j
y_j
yj是其当前状态的函数, M-P 模型的数学表达式为: 
式中,
θ
j
θ_j
θj为阈值,
s
g
n
sgn
sgn是符号函数。当净输入超过阈值时,
y
j
y_j
yj取+1 输出,反之为-1输出 。如果考虑输出与输入的延时作用,表达式可修正为:

3.ANN的基本要素
- 神经元激活函数
- 网络的学习
- 神经元之间的连接形式
(1)常用激活函数

(2)常用学习规则
- Hebb规则
- 误差修正法学习算法 (如:BP算法)
- 胜者为王(Winner-Take-All)学习规则
(3)神经元之间连接方式
<1>前缀网络

<2>反馈网络

> 注:BP 神经网络属于前缀网络
二、 BP 神经网络原理
BP(Back Propagation)神经网络的学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经隐层逐层处理后,传向输出层。若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。BP网络由输入层﹑输出层和隐层组成,
N
1
N_1
N1 为输入层,
N
m
N_m
Nm为输出层,其余为隐层。BP 神经网络的结构如下:

这里介绍三层神经网络的推导(一个输入层、一个隐层和一个输出层)
BP 神经网络反向传播算法的神经元示意图图一:

上图描绘了神经元 j j j被它左边的一层神经元产生的一组函数信号所馈给。 m m m是作用于神经元 j j j的所有输入不包括偏置的个数。突触权值 w j 0 ( n ) w_{j0}(n) wj0(n)等于神经元 j j j的偏置 b j b_j bj。
1.前向传播过程推导
图一中,在神经元
j
j
j的激活函数输入处产生的诱导局部域
v
j
(
n
)
v_j(n)
vj(n)(即神经元
j
j
j 的输入)是:

ϕ
j
\phi_j
ϕj是激活函数,则出现在神经元
j
j
j输出处的函数信号(即神经元
j
j
j的输出)
y
j
(
n
)
y_j(n)
yj(n)是:

2.误差反向传播过程推导
在图一中, y j ( n ) y_j(n) yj(n)与 d j ( n ) d_j(n) dj(n)分别是神经元 j j j的实际输出和期望输出,则神经元 j j j的输出所产生的误差信号定义为:

其中,
d
j
(
n
)
d_j(n)
dj(n)是期望响应向量
d
(
n
)
d(n)
d(n)的第
j
j
j个元素。
为了使函数连续可导,这里最小化均方根差,定义神经元
j
j
j的瞬时误差能量为:

将所有输出层神经元的误差能量相加,得到整个网络的全部瞬时误差能量:

其中,集合C 包括输出层的所有神经元。
BP 算法通过反复修正权值使式(2-5)
E
n
E_n
En最小化,采用梯度下降法对突触权值
w
j
i
(
n
)
w_{ji}(n)
wji(n)应用一个修正值
∆
w
j
i
(
n
)
∆w_{ji}(n)
∆wji(n)它正比于偏导数
δ
\delta
δ
E
(
n
)
/
E(n)/
E(n)/
δ
\delta
δ
w
j
i
(
n
)
w_{ji}(n)
wji(n)。根据微分链式规则,把这个梯度表示为:
偏导数
δ
\delta
δ
E
(
n
)
/
E(n)/
E(n)/
δ
\delta
δ
w
j
i
(
n
)
w_{ji}(n)
wji(n)代表一个敏感因子,决定突触权值
w
j
i
w_{ji}
wji在权值空间的搜索方向。
在式(2-5)两边对
e
j
(
n
)
e_j(n)
ej(n)取微分,得到:

在式(2-3)两边对
y
j
(
n
)
y_j(n)
yj(n)取微分,得到:

在式(2-2)两边对
v
j
(
n
)
v_j(n)
vj(n)取微分,得到:

最后在式(2-1)两边对
w
j
i
(
n
)
w_{ji}(n)
wji(n)取微分,得到:

将式(2-7)——(2-10)带入式(2-6)得:

应用于
w
j
i
(
n
)
w_{ji}(n)
wji(n)的修正
∆
w
j
i
(
n
)
∆w_{ji}(n)
∆wji(n)定义为:

其中, η \eta η是误差反向传播的学习率, 负号表示在权空间中梯度下降。
将式(2-11)带入式(2-12)得:

其中,
δ
j
(
n
)
\delta_j(n)
δj(n)是根据delta法则定义的局部梯度:

局部梯度指明了突触权值所需要的变化。
现在来考虑神经元 j j j所处的层。
####(1) 神经元
j
j
j是输出层节点
当神经元
j
j
j位于输出层时,给它提供了一个期望响应。根据式(2-3)误差信号
e
j
(
n
)
=
d
j
(
n
)
−
y
j
(
n
)
e_j(n)=d_j(n)-y_j(n)
ej(n)=dj(n)−yj(n)确定,通过式(2-14)得到神经元
j
j
j的局部梯度
δ
j
(
n
)
\delta_j(n)
δj(n)为:

####(2) 神经元
j
j
j是隐层节点
当神经元
j
j
j位于隐层时,没有对该输入神经元的指定期望响应。隐层的误差信号要根据所有与隐层神经元直接相连的神经元的误差信号向后递归决定。
考虑神经元
j
j
j为隐层节点,隐层神经元的局部梯度
δ
j
(
n
)
\delta_j(n)
δj(n)根据式(2-14)重新定义为:

来看图二:它表示输出层神经元
k
k
k连接到隐层神经元
j
j
j的信号流图。

在这里下标
j
j
j表示隐层神经元,下标
k
k
k表示输出层神经元。
图二中,网络的全部瞬时误差能量为:

在式(2-17)两边对函数信号
y
j
(
n
)
y_j(n)
yj(n)求偏导,得到:

在图二中:

因此,

图二中,对于输出层神经元
k
k
k ,其诱导局部域是:

求式(2-21)对
y
j
(
n
)
y_j(n)
yj(n)的微分得到:

将式(2-20)和(2-22)带入到式(2-18)得到:

将式(2-23)带入式(2-16)得隐层神经元
j
j
j的局部梯度
δ
j
(
n
)
\delta_j(n)
δj(n)为:

反向传播过程推导总结
因此,结合式(2-13)、(2-15)和(2-24),由神经元 i i i连接到神经元 j j j的突触权值的修正值 ∆ w j i ( n ) ∆w_{ji}(n) ∆wji(n)按照delta法则定义如下:

其中:
- 神经元 j j j是输出层节点时,局部梯度 δ j ( n ) \delta_j(n) δj(n)等于倒数 ϕ j ′ ( v j ( n ) ) \phi_j'(v_j(n)) ϕj′(vj(n))和误差信号 e j ( n ) = d j ( n ) − y j ( n ) e_j(n)=d_j(n)-y_j(n) ej(n)=dj(n)−yj(n)的乘积,见式(2-15);
- 神经元 j j j是隐层节点时,局部梯度 δ j ( n ) \delta_j(n) δj(n)等于倒数 ϕ j ′ ( v j ( n ) ) \phi_j'(v_j(n)) ϕj′(vj(n))和下一层(隐层或输出层)的 δ k \delta_k δk与权值加权和的乘积,见式(2-24)。
3.标准BP神经网络设计原则
(1)激活函数
单极性S型函数和双曲正切S型函数
(2)学习率
0
<
η
<
1
0<\eta<1
0<η<1
(3)停止准则
网络的均方误差足够小或者训练足够的次数等
(4)初始权值
以均值等于0的均匀分布随机挑选突触权值
(5)隐层结构
理论证明一个隐层就能映射所有连续函数 ;
隐层节点数=
(
输
入
节
点
数
+
输
出
节
点
数
)
\sqrt{(输入节点数+输出节点数)}
(输入节点数+输出节点数) +
α
\alpha
α,
1
<
α
<
10
1<\alpha<10
1<α<10 或
隐层节点数= ( 输 入 节 点 数 ∗ 输 出 节 点 数 ) \sqrt{(输入节点数*输出节点数)} (输入节点数∗输出节点数)
4.标准BP算法训练过程及流程图
(1)训练过程
-
初始化网络的突触权值和阈值矩阵;
-
训练样本的呈现;
-
前向传播计算;
-
误差反向传播计算并更新权值;
-
迭代,用新的样本进行步骤3和4,直至满足停止准则。
(2)流程图

5.标准BP算法分析
由于标准 BP 算法采用的是梯度下降法,BP 算法的 E-w 曲线图如下:

因此标准 BP 算法具有以下缺陷:
- 在误差曲面上有些区域平坦,此时误差对权值的变化不敏感,误差下降缓慢,调整时间长,影响收敛速度。
- 存在多个极小点,梯度下降法容易陷入极小点而无法得到全局最优解。
- 学习率 η \eta η越小,学习速度减慢,而 η \eta η越大,虽然学习速度加快,却容易使权值的变化量不稳定,出现振荡。
6.标准BP算法改进方法
(1)增加动量项
一个既要加快学习速度又要保持稳定的方法是修改式(2-13),增加动量项,表示为:

这里
α
\alpha
α是动量常数,0≤
α
\alpha
α<1。
动量项 α ∆ w j i ( n − 1 ) \alpha∆w_{ji}(n-1) α∆wji(n−1)反映了以前积累的调整经验,当误差梯度出现局部极小时,虽然 ∆ w j i ( n ) ∆w_{ji}(n) ∆wji(n)→0,但 ∆ w j i ( n − 1 ) ∆w_{ji}(n-1) ∆wji(n−1)≠0,使其跳出局部极小区域,加快迭代收敛速度。
(2)其他改进方法
- 可变学习速度的反向传播
- 学习速率的自适应调节
- 引入陡度因子——防止饱和
- 共轭梯度法、拟牛顿法等








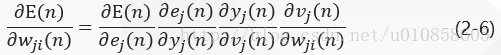
















 4362
4362

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








