Devillers & Guigue算法( 简称Devillers 算法) 通过三角形各顶点构成的行列式正负的几何意义来判断三角形中点、线、面之间的相对位置关系,从而判断两三角形是否相交。其基本原理如下:给定空间四个点:a(ax,ay,az),b=(bx,by,bz),c=(cx,cy,cz),d=(dx,dy,dz),定义行列式如下:
[ a, b, c, d] 采用右手螺旋法则定义了四个空间点的位置关系。[ a, b, c, d] > 0 表示 d 在 a、b、c 按逆时针顺序所组成的三角形的正法线方向( 即上方) ; [ a, b, c, d] < 0 表示 d 在 △abc的下方; [ a, b, c, d] = 0 表示四点共面。
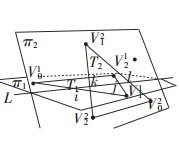
设两个三角形T1和T2,顶点分别为:V10,V11,V12和V20,V21,V22,三角形所在的平面分别为π1和π2,其法向量分别为N1和N2.算法先判别三角形和另一个三角形所在的平面的相互位置关系,提前排除不相交的情况。通过计算[V20,V21,V22,V1i].(i=0,1,2)来判断T1和π2的关系:如果所有的行列式的值都不为零且同号,则T1和T2不相交;否则T1和π2相交。相交又分为如下几种情况:
a)如果所有的行列式的值为零,则T1和T2共面,转化为共面的线段相交问题。
b)如果其中一个行列式的值为零,而其他两个行列式同号,则只有一个点在平面内,测试顶点是否则T2内部,是则相交,否则不相交;
c)否则T1的顶点位于平面π2两侧(包含T1的一条边在平面π2中的情况)。
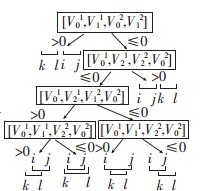
再按照类似的方法对 T 2 和 π 1 作进一步的测试。如果通过测试, 则每个三角形必有确定的一点位于另一个三角形所在平面的一侧, 而另外两点位于其另一侧。算法分别循环置换每个三角形的顶点, 以使V10(V20)位于π2(π1)的一侧,另两个点位于其另一侧;同时对顶点V21,V22(V11,V12)进行交换操作,以确保V10(V20)位于π2(π1)的上方,即正法线方向。经过以上的预排除和置换操作,V10的邻边V10V11,V10V12和V20的邻边V20V21和V20V22与两平面的交线L相交于固定形式的点上,分别记为i,j,k,l(i<j,k<l),如图:
[V10,V11,V20,V21]<=0 && [V10,V12,V22,V20]<=0 (1)
- typedef float float3[3];
- enum TopologicalStructure
- {
- INTERSECT, NONINTERSECT
- };
- struct Triangle
- {
- float3 Normal_0;
- float3 Vertex_1, Vertex_2, Vertex_3;
- };
- struct point
- {
- float x, y;
- };
- //四点行列式
- inline float get_vector4_det( float3 v1, float3 v2, float3 v3, float3 v4 )
- {
- float a[3][3];
- for ( int i = 0; i != 3; ++i )
- {
- a[0][i] = v1[i] - v4[i];
- a[1][i] = v2[i] - v4[i];
- a[2][i] = v3[i] - v4[i];
- }
- return a[0][0] * a[1][1] * a[2][2]
- + a[0][1] * a[1][2] * a[2][0]
- + a[0][2] * a[1][0] * a[2][1]
- - a[0][2] * a[1][1] * a[2][0]
- - a[0][1] * a[1][0] * a[2][2]
- - a[0][0] * a[1][2] * a[2][1];
- }
- //利用叉积计算点p相对线段p1p2的方位
- inline double direction( point p1, point p2, point p ){
- return ( p.x - p1.x ) * ( p2.y - p1.y ) - ( p2.x - p1.x ) * ( p.y - p1.y ) ;
- }
- //确定与线段p1p2共线的点p是否在线段p1p2上
- inline int on_segment( point p1, point p2, point p ){
- double max = p1.x > p2.x ? p1.x : p2.x ;
- double min = p1.x < p2.x ? p1.x : p2.x ;
- double max1 = p1.y > p2.y ? p1.y : p2.y ;
- double min1 = p1.y < p2.y ? p1.y : p2.y ;
- if ( p.x >= min && p.x <= max && p.y >= min1 && p.y <= max1 )
- {
- return 1;
- }
- else
- {
- return 0;
- }
- }
- //判断线段p1p2与线段p3p4是否相交的主函数
- inline int segments_intersert( point p1, point p2, point p3, point p4 ){
- double d1, d2, d3, d4;
- d1 = direction( p3, p4, p1 );
- d2 = direction( p3, p4, p2 );
- d3 = direction( p1, p2, p3 );
- d4 = direction( p1, p2, p4 );
- if ( d1 * d2 < 0 && d3 * d4 < 0 )
- {
- return 1;
- }
- else if ( d1 == 0 && on_segment( p3, p4, p1 ) == 1 )
- {
- return 1;
- }
- else if ( d2 == 0 && on_segment( p3, p4, p2 ) == 1 )
- {
- return 1;
- }
- else if ( d3 == 0 && on_segment( p1, p2, p3 ) == 1 )
- {
- return 1;
- }
- else if ( d4 == 0 && on_segment( p1, p2, p4 ) == 1 )
- {
- return 1;
- }
- return 0;
- }
- //判断同一平面的直线和三角形是否相交
- inline bool line_triangle_intersert_inSamePlane( Triangle* tri, float3 f1, float3 f2 )
- {
- point p1, p2, p3, p4;
- copy_point( p1, f1 );
- copy_point( p2, f2 );
- copy_point( p3, tri->Vertex_1 );
- copy_point( p4, tri->Vertex_2 );
- if ( segments_intersert( p1, p2, p3, p4 ) )
- {
- return true;
- }
- copy_point( p3, tri->Vertex_2 );
- copy_point( p4, tri->Vertex_3 );
- if ( segments_intersert( p1, p2, p3, p4 ) )
- {
- return true;
- }
- copy_point( p3, tri->Vertex_1 );
- copy_point( p4, tri->Vertex_3 );
- if ( segments_intersert( p1, p2, p3, p4 ) )
- {
- return true;
- }
- return false;
- }
- //判断同一平面内的三角形是否相交
- inline bool triangle_intersert_inSamePlane( Triangle* tri1, Triangle* tri2 )
- {
- if ( line_triangle_intersert_inSamePlane( tri2, tri1->Vertex_1, tri1->Vertex_2 ) )
- {
- return true;
- }
- else if ( line_triangle_intersert_inSamePlane( tri2, tri1->Vertex_2, tri1->Vertex_3 ) )
- {
- return true;
- }
- else if ( line_triangle_intersert_inSamePlane( tri2, tri1->Vertex_1, tri1->Vertex_3 ) )
- {
- return true;
- }
- else
- {
- return false;
- }
- }
- //向量之差
- inline void get_vector_diff( float3& aimV, const float3 a, const float3 b )
- {
- aimV[0] = b[0] - a[0];
- aimV[1] = b[1] - a[1];
- aimV[2] = b[2] - a[2];
- }
- //向量内积
- inline float Dot( const float3& v1, const float3& v2 )
- {
- return v1[0] * v2[0] + v1[1] * v2[1] + v1[2] * v2[2] ;
- }
- //重心法判断点是否在三角形内部
- inline bool is_point_within_triangle( Triangle* tri, float3 point )
- {
- float3 v0;
- get_vector_diff( v0, tri->Vertex_1, tri->Vertex_3 );
- float3 v1;
- get_vector_diff( v1, tri->Vertex_1, tri->Vertex_2 );
- float3 v2;
- get_vector_diff( v2, tri->Vertex_1, point );
- float dot00 = Dot( v0, v0 ) ;
- float dot01 = Dot( v0, v1 ) ;
- float dot02 = Dot( v0, v2 ) ;
- float dot11 = Dot( v1, v1 ) ;
- float dot12 = Dot( v1, v2 ) ;
- float inverDeno = 1 / ( dot00* dot11 - dot01* dot01 ) ;
- float u = ( dot11* dot02 - dot01* dot12 ) * inverDeno ;
- if ( u < 0 || u > 1 ) // if u out of range, return directly
- {
- return false ;
- }
- float v = ( dot00* dot12 - dot01* dot02 ) * inverDeno ;
- if ( v < 0 || v > 1 ) // if v out of range, return directly
- {
- return false ;
- }
- return u + v <= 1 ;
- }
- //Devillers算法主函数
- inline TopologicalStructure judge_triangle_topologicalStructure( Triangle* tri1, Triangle* tri2 )
- {
- //设tri1所在的平面为p1,tri2所在的平面为p2
- float p1_tri2_vertex1 = get_vector4_det( tri1->Vertex_1, tri1->Vertex_2, tri1->Vertex_3, tri2->Vertex_1 );
- float p1_tri2_vertex2 = get_vector4_det( tri1->Vertex_1, tri1->Vertex_2, tri1->Vertex_3, tri2->Vertex_2 );
- float p1_tri2_vertex3 = get_vector4_det( tri1->Vertex_1, tri1->Vertex_2, tri1->Vertex_3, tri2->Vertex_3 );
- if ( p1_tri2_vertex1 > 0 && p1_tri2_vertex2 > 0 && p1_tri2_vertex3 > 0 )
- {
- return NONINTERSECT;
- }
- if ( p1_tri2_vertex1 < 0 && p1_tri2_vertex2 < 0 && p1_tri2_vertex3 < 0 )
- {
- return NONINTERSECT;
- }
- if ( p1_tri2_vertex1 == 0 && p1_tri2_vertex2 == 0 && p1_tri2_vertex3 == 0 )
- {
- if ( triangle_intersert_inSamePlane( tri1, tri2 ) )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
- if ( p1_tri2_vertex1 == 0 && p1_tri2_vertex2 * p1_tri2_vertex3 > 0 )
- {
- if ( is_point_within_triangle( tri1, tri2->Vertex_1 ) )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
- else if ( p1_tri2_vertex2 == 0 && p1_tri2_vertex1 * p1_tri2_vertex3 > 0 )
- {
- if ( is_point_within_triangle( tri1, tri2->Vertex_2 ) )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
- else if ( p1_tri2_vertex3 == 0 && p1_tri2_vertex1 * p1_tri2_vertex2 > 0 )
- {
- if ( is_point_within_triangle( tri1, tri2->Vertex_3 ) )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
- float p2_tri1_vertex1 = get_vector4_det( tri2->Vertex_1, tri2->Vertex_2, tri2->Vertex_3, tri1->Vertex_1 );
- float p2_tri1_vertex2 = get_vector4_det( tri2->Vertex_1, tri2->Vertex_2, tri2->Vertex_3, tri1->Vertex_2 );
- float p2_tri1_vertex3 = get_vector4_det( tri2->Vertex_1, tri2->Vertex_2, tri2->Vertex_3, tri1->Vertex_3 );
- if ( p2_tri1_vertex1 > 0 && p2_tri1_vertex2 > 0 && p2_tri1_vertex3 > 0 )
- {
- return NONINTERSECT;
- }
- if ( p2_tri1_vertex1 < 0 && p2_tri1_vertex2 < 0 && p2_tri1_vertex3 < 0 )
- {
- return NONINTERSECT;
- }
- if ( p2_tri1_vertex1 == 0 && p2_tri1_vertex2 * p2_tri1_vertex3 > 0 )
- {
- if ( is_point_within_triangle( tri2, tri1->Vertex_1 ) )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
- if ( p2_tri1_vertex2 == 0 && p2_tri1_vertex1 * p2_tri1_vertex3 > 0 )
- {
- if ( is_point_within_triangle( tri2, tri1->Vertex_2 ) )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
- if ( p2_tri1_vertex3 == 0 && p2_tri1_vertex1 * p2_tri1_vertex2 > 0 )
- {
- if ( is_point_within_triangle( tri2, tri1->Vertex_3 ) )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
- float* tri1_a = tri1->Vertex_1,* tri1_b = tri1->Vertex_2,* tri1_c = tri1->Vertex_3
- ,* tri2_a = tri2->Vertex_1,* tri2_b = tri2->Vertex_2,* tri2_c = tri2->Vertex_3;
- float* m;
- float im;
- if ( p2_tri1_vertex2 * p2_tri1_vertex3 >= 0 && p2_tri1_vertex1 != 0 )
- {
- if ( p2_tri1_vertex1 < 0 )
- {
- m = tri2_b;
- tri2_b = tri2_c;
- tri2_c = m;
- im = p1_tri2_vertex2;
- p1_tri2_vertex2 = p1_tri2_vertex3;
- p1_tri2_vertex3 = im;
- }
- }
- else if ( p2_tri1_vertex1 * p2_tri1_vertex3 >= 0 && p2_tri1_vertex2 != 0 )
- {
- m = tri1_a;
- tri1_a = tri1_b;
- tri1_b = tri1_c;
- tri1_c = m;
- if ( p2_tri1_vertex2 < 0 )
- {
- m = tri2_b;
- tri2_b = tri2_c;
- tri2_c = m;
- im = p1_tri2_vertex2;
- p1_tri2_vertex2 = p1_tri2_vertex3;
- p1_tri2_vertex3 = im;
- }
- }
- else if ( p2_tri1_vertex1 * p2_tri1_vertex2 >= 0 && p2_tri1_vertex3 != 0 )
- {
- m = tri1_a;
- tri1_a = tri1_c;
- tri1_c = tri1_b;
- tri1_b = m;
- if ( p2_tri1_vertex3 < 0 )
- {
- m = tri2_b;
- tri2_b = tri2_c;
- tri2_c = m;
- im = p1_tri2_vertex2;
- p1_tri2_vertex2 = p1_tri2_vertex3;
- p1_tri2_vertex3 = im;
- }
- }
- if ( p1_tri2_vertex2 * p1_tri2_vertex3 >= 0 && p1_tri2_vertex1 != 0 )
- {
- if ( p1_tri2_vertex1 < 0 )
- {
- m = tri1_b;
- tri1_b = tri1_c;
- tri1_c = m;
- }
- }
- else if ( p1_tri2_vertex1 * p1_tri2_vertex3 >= 0 && p1_tri2_vertex2 != 0 )
- {
- m = tri2_a;
- tri2_a = tri2_b;
- tri2_b = tri2_c;
- tri2_c = m;
- if ( p1_tri2_vertex2 < 0 )
- {
- m = tri1_b;
- tri1_b = tri1_c;
- tri1_c = m;
- }
- }
- else if ( p1_tri2_vertex1 * p1_tri2_vertex2 >= 0 && p1_tri2_vertex3 != 0 )
- {
- m = tri2_a;
- tri2_a = tri2_c;
- tri2_c = tri2_b;
- tri2_b = m;
- if ( p1_tri2_vertex3 < 0 )
- {
- m = tri1_b;
- tri1_b = tri1_c;
- tri1_c = m;
- }
- }
- if ( get_vector4_det( tri1_a, tri1_b, tri2_a, tri2_b ) <= 0 && get_vector4_det( tri1_a, tri1_c, tri2_c, tri2_a ) <= 0 )
- {
- return INTERSECT;
- }
- else
- {
- return NONINTERSECT;
- }
- }
参考资料:
[1] 空间三角形快速相交检测算法 邹益胜, 丁国富, 何邕, 许明恒( 西南交通大学 机械工程学院)
[2] http://www.cnblogs.com/graphics/archive/2010/08/05/1793393.html










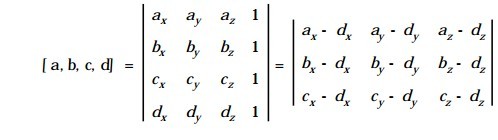














 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








