重新回顾概率统计过程:
Data→Model→ Decision
实际工程中,就是从这三点出发,走完概率统计的整个过程。
这里要清楚数据是上帝给的,模型是人造的,不可避免存在各种各样的问题。数据到模型这个过程就叫做统计statistic。Data就是采样samples,信号的结构,关键参数。我们希望通过采样,让我们不清楚的东西变得清楚。
目录
二、统计最优性(Optimality in Statistic)
4、最小均方误差(Minimum Mean Square Error,MMSE)
4.2、uniformly minimum variance
5.1、充分统计量(Sufficient Statistic)
一、一个例子(说明统计过程)
1、建立统计
一个直流分量A,A是未知量。采样为![]() ,
,![]() 绝大多数情况下都不是A,跟A之间一定差着某种噪声。
绝大多数情况下都不是A,跟A之间一定差着某种噪声。
![]()
![]() ,
,![]() ,采样两次相加,噪声相加就会变小。所以不仅要相加,而且还要除2,这个除2其实就是信号处理的过程(利用数学手段,对所采集带的数据进行计算)。在这里需要对观念进行梳理:N为随机变量,A为确定常数,X为随机变量。
,采样两次相加,噪声相加就会变小。所以不仅要相加,而且还要除2,这个除2其实就是信号处理的过程(利用数学手段,对所采集带的数据进行计算)。在这里需要对观念进行梳理:N为随机变量,A为确定常数,X为随机变量。
![]()
2、使得统计的方差变小
检查一下方差是否变小(就是为了让方差变小),令
![]()
准备工作:给噪声建模型,![]() 。
。
![]()
![]()
则![]() ,
,
![]()
![]()
![]()
![]()
需要加入独立性假设,不独立有些复杂。
![]()
因此,通过两次采样,并作了一下“处理”,我们所得到的方差的确减小了。独立使得方差得以减小,所以每次实验都要把实验装置清零。
 假设搞了N次实验
假设搞了N次实验

方差仅代表处理结果自身的抖动,所以还要看一下均值。
![]()
由线性性,均值的平均=平均的均值=0。看起来这个估计还是相当不错的。但是到现在位置,还是没名没份的,还是我们拍脑袋拍出来的。
二、统计最优性(Optimality in Statistic)
希望能够建立起统计当中的某种最优性(Optimality in Statistic)、同时把这种最优性当作指导方针,贯彻到之后的学习中。所以,需要:
1、参数化模型(Parametric Model)
我们的采样要服从某种分布![]()
![]()
![]()
我们采样的目的就是进行计算,从而确定这个未知参数,使这个参数尽可能靠谱。
在上一个例子中,我们并没有知道噪声的分布。所以假设噪声是高斯的,然后验证一下。
2、损失函数
![]()
![]()
![]()
计算估计和实际的损失。![]() ,是采样的函数。上述两点全部都是先验知识(Prior Knowledge)这个先验知识:
,是采样的函数。上述两点全部都是先验知识(Prior Knowledge)这个先验知识:
- 来源于工程背景,背景会影响模型产出
- 来源于经验
- 建模时往往会屈从于能力不足,因为复杂模型建了之后处理不了
1、Mean Square Error(MSE)
![]()
找到一种运算,使得这个均方误差最小。因为![]() 也随机变量,简单分析一下:
也随机变量,简单分析一下:
![]()
![]()
![]()
![]() 是确定值,所以可以提出来,所以有
是确定值,所以可以提出来,所以有![]() 。
。![]() ,因为统计意义上,这个必须是0。
,因为统计意义上,这个必须是0。
我们从未真正懂得过什么,我们只是在习惯什么。
--冯∙
诺伊曼
因此上式为:
![]()
![]()
要在方差和偏差之间做出Tradeoff,Bias Variance Tradeoff
因为在数学上是平等的,但是在实际应用中可能差很多。但还是希望方差最小。因为,偏差代表的是系统误差(System Error),方差是随机误差(Random Error),系统误差很容易通过系统的方法矫正掉。
所以一般我们假定我们的估计是无偏的。接下来介绍无偏性。
3、无偏性
![]()
现在进行了N次采样,![]() ,使用
,使用![]() ,均方误差用下式来估计:
,均方误差用下式来估计:
![]()

上式中的一个条件是,连续的测量一个量,测量的结果取平均,肯定是无偏的,因为每一个是无偏的,噪声的均值是0,所以后面那一项等于0
上式实现不了,因为![]() 根本就不知道,在实验中都有经验,如果theta不知道,可以用“样本均值”进行取代,但是一道用样本均值进行取代,前面系数是要变化的(变为N-1,为了满足无偏性条件)。
根本就不知道,在实验中都有经验,如果theta不知道,可以用“样本均值”进行取代,但是一道用样本均值进行取代,前面系数是要变化的(变为N-1,为了满足无偏性条件)。

无偏性证明



因为i.i.d条件,因此上式


![]()
![]()
![]()
上式中2![]() ,而
,而![]() 共有(N-1)项。
共有(N-1)项。
定性思考:为什么是N-1?因为:从![]() 到
到![]() 自由度是减小的。
自由度是减小的。
4、最小均方误差(Minimum Mean Square Error,MMSE)
进一步定义最优:我们希望能够极小化MSE(Minimum Mean Square Error,MMSE)
![]()
4.1、 uniformly MMSE
希望找到uniformly MMSE,对任意![]() 适用。(EG:神医和糖尿病,只看一点,不及其余,只看一眼,说谁都有糖尿病,总有说对的时候。)
适用。(EG:神医和糖尿病,只看一点,不及其余,只看一眼,说谁都有糖尿病,总有说对的时候。)
![]()
医师资格考试,每一科都要大于均值,对应的就是无偏性,(在每一个theta上,都要满足均值为0)![]() 。
。
4.2、uniformly minimum variance
在无偏的基础上,重新看uniformly MMSE,就变成方差了,因为偏差没有了(uniformly minimum variance,UMV)。
三、条件期望
条件期望![]() 以X为条件的Y期望,是随机变量(无条件期望是确定性参数)。Y是期望的对象,在E的过程中被E掉了,但是|右边X仍然是随机变量,并没有因为E消失,仍保留一定随机性;观念要灵活,对于随机性的看法,在对条件期望的理解上要进行转换,在计算Y的期望的时候,X(先验、已知)起到的作用是随机性暂时消失,可以认为是确定的。计算完成后再暴露出其随机性,再处理就变简单了。
以X为条件的Y期望,是随机变量(无条件期望是确定性参数)。Y是期望的对象,在E的过程中被E掉了,但是|右边X仍然是随机变量,并没有因为E消失,仍保留一定随机性;观念要灵活,对于随机性的看法,在对条件期望的理解上要进行转换,在计算Y的期望的时候,X(先验、已知)起到的作用是随机性暂时消失,可以认为是确定的。计算完成后再暴露出其随机性,再处理就变简单了。
举个例子:![]() 是独立同分布的,我们计算其和的分布
是独立同分布的,我们计算其和的分布![]()
现在N变成随即量,同样计算其和的分布,如果沿用刚才的结果
![]()
应该是
![]()
条件期望的两个重要性质:(从这里开始到条件方差之前都还没有弄很懂)
1、![]()
2、 ![]()
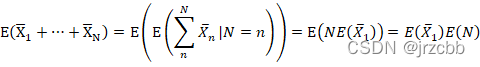
条件期望与最小均方误差的关系,最优化:
![]()
能够对Y进行估计得最优X构成的统计,是条件期望
![]()
![]()
要证明交叉项为0。把X条件住,随机属性分析,X条件住可以确定三项
![]()
![]()
其中(由线性性)
![]()
![]()
因此交叉项为0。
四、条件方差
条件期望再期望就是无条件期望,
![]()
但方差不是,方差是2阶,方差的方差是4阶?
什么是条件方差?是一个随机变量,
![]()
无条件方差为
![]()
![]()
![]()
![]()
![]()
![]()
五、充分统计量和UMMSE
5.1、充分统计量(Sufficient Statistic)
![]()
对其进行处理,尽可能包含![]() theta的信息。举例说明:
theta的信息。举例说明:
Eg1:假定![]() 估计均值。
估计均值。
令
![]()
对估计有帮助吗?均值等于相减,方差为相加,因此
![]()
这个统计根本没用,因为theta没有了,(Ancillary,多余的)
Eg2:假定fx,θ=U0,θ![]()
令
θ1X=minX1,…,XN ![]()
θ2X=maxX1,…,XN![]()
肯定是2更好,因为更接近theta。
问题来了:有没有这样的统计,把Theta相关信息补干净。浓缩了采样数据中所有的信息,不会丢失掉有关theta

![]()
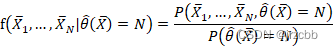

上式跟theta无关。
最优估计:
万事俱备,接下来计算最优。给出求最优估计的过程(Optimizing Procedure)。
![]()
![]()
![]()
![]()
断言,theta3也是无偏的。
![]()
![]()
![]()
以上为Rao-Blackwell定理。可以通过这个过程缩小方差。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








