现代信号处理笔记 3 估计误差下界

现代数字信号处理1 2019 张颢 06 第三讲1 现代数字信号处理1 - YouTube

---

目录 ​​​​​​​

---

完备统计

定义 

Lehmam-Scheffe Theorem

误差估计下界(Cramer-Rao Lower Bound)

 一个例子

第一步：写出模型

 第二步：求log

 第三步：求两次导数

第四步：求Fisher Information和Lower Bound

 另一个例子：讨论下界能否达到

 另一种下界推算方法

一个例子（高斯噪声，回波延时估计）

---

假设样本已经在手里了，且i.i.d，希望用这些样本构成一个分布，求未知参数，这个叫参数化模型。求位置参数就形成了“估计”。估计是信号处理的结果，希望尽可能接近我们想要的参数，因此想要找到最小误差的估计，这里误差采用的是均方误差。而且需要找到对于所有数据都适用的估计uniform。并且希望估计具有无偏性，也就是最小方差无偏估计（Minimum Variance Unbiased Error，MVUE）。

如何找到最小方差？Rao-Blackwell Procedure，形成新的估计，比原有的估计方差要小。也就是条件期望。

这个小？有没有尽头？这是本节课的需求。

完备统计

定义 

Complete Statistics：

一个统计T（一个依赖样本的函数）是完备的，指的是这个统计内已经不包含任何与参数θ 无关的信息。就好比一个人是完备的，一块肥肉都没有，脂肪含量0%。一般只存在于纸面上，不太可能在现实中出现，但是这是我们的目标，我们的估计最好可以做到完备估计。

举了个切肥肉的例子15：00，不理解。

Lehmam-Scheffe Theorem

假定S是一个统计， ，构造一个新的统计T，这个T是充分且完备的估计：

这个估计有理论上的最小方差。

任取一个估计

验证：

1. 
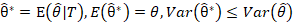
2. 接下来用完备性说明theta*和S*是一回事，因为两个都是无偏估计，所以

       是T的一个函数。

       所以 一定是MVUE。

误差估计下界(Cramer-Rao Lower Bound)

需要正则化条件，但是这里我们默认成立。

Lower Bound of Estimation Error但未必是下确界。

Sigma确定。

图1 模型的胖瘦

图2 下确界示意图

红色会估计的更准确，因为方差小（胖瘦）。但是用曲率（Curvature，内接圆的半径的倒数）描述更为准确，也就是曲线顶点的曲率要大。曲率一定是跟二阶导数有关的。

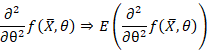
将随机变量变成正常的。

一阶导数是变化率，跟变化的快慢，变化的越快，越相关，稍微一动，统计和数据会有巨大变化，参数与采样越依赖(我们希望发生这样的事情)。本质上关注的是绝对值，但是绝对值处理不方便，所以要平方一下。

估计的下界到底在哪里？先看几个基本事实

注意是对x的积分。

（积分肯定是1，所以微分肯定是0，我们是工科院校，所以不要在意交换积分顺序，实际上是需要条件的，但是我们假设想要的都有。）

进而，有，

使用柯西不等式，线性代数中有一个内积

存在对成性和非负性。还具有双线性(Bilinear)：

考察空间的内积

如果我的线性空间是平方可积的函数的话，

Cauchy-Schwarz是内积最重要的性质：

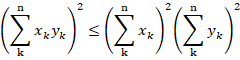
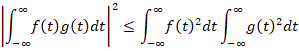
含义非常深刻，绝不仅仅是线性空间的一个几何上的概念，在物理上也有，测不准原理本质上就是柯西施瓦兹不等式。证明：

则 

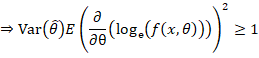
和一阶导数比较像，因为log是单调的，所以不改变什么。
越大越低。这就是著名的Cramer-Rao Lower Bound. （Rao-Blackwell还是之前那个印度学者）

就是Fisher Information

估计本身是由下界的，跟统计方法有关。

我们对于二阶导数的感觉也是对的。

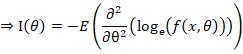
 一个例子

计算Fisher Information

第一步：写出模型

Joint Distrubution（Model）

 第二步：求log

 第三步：求两次导数

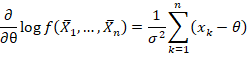
第四步：求Fisher Information和Lower Bound

 可以，柯拉梅洛界就是，如果一个估计是无偏的，则其方差

 另一个例子：讨论下界能否达到

这个下界能否达到？当然可以，求平均

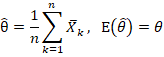
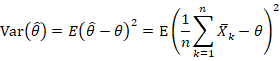
 有效（Efficient）估计是指可以达到CRLB的估计。有兴趣可以了解一下Fibre Bundle杨振宁的工作。

 另一种下界推算方法

柯西不等式在随机变量上的形式：

这里把相关当作内积，线性、非负性、双线性

因此，

 这还不是下界，因为右端和还有关系。使用一个恰当的，使得右端与估计无关。

则

现在计算

则（1）有

​​​​​CRLB的小变种，冲着X的某个函数去考虑

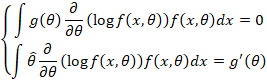
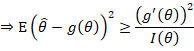
一个例子（高斯噪声，回波延时估计）

 假定 ，是采样数据，由两部分构成，一部分是，参数，我要估计的东西，是接收到的信号，具有一定的形式（雷达声纳导航等），用CRLB写paper非常容易发表，显得很理论，一个形式一篇文章。噪声一般是高斯的，97/100的文章都是用高斯噪声。

​​​​​​​怎么计算 和CLRB？

四部曲：

第一步：首先写分布，假设Xiid

第二步：取log

第三步：求导，一次二次都可以，哪个方便用哪个。

明显不能再求了，已经很复杂了

第四步：

​​​​​​​

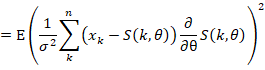
真正有随机性的只有x_k，而且交叉项肯定为0

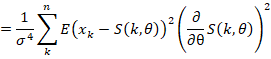
因为 

所以 

之后稍微具体化一下，做一个Range Estimation，估计回波时延。

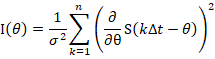
接收过程 

 因此我们知道， ，重新总结Fisher信息量，因此只有m个有效样本。
 

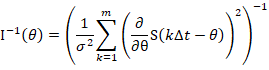
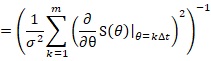
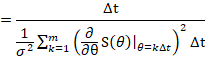
准备用微积分的方法，来近似

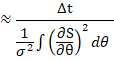
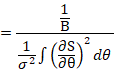
， 为功率谱密度。

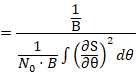
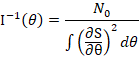
进行一点儿傅里叶分析，对于任意信号S而言，如果S的傅里叶变换为 （读S飘），则

使用帕斯瓦尔等式（Par）：

因此傅里叶变换是U变换，是正交的

所以，

分母就叫做有效带宽Effective Bandwidth（波形S的）。

这就是雷达原理的基本结论，估计精度取决于噪声大小，取决于信号的带宽。