独立样本t检验、方差齐性检验

什么是独立样本t检验？
t检验是比较两组数据之间的差异，有无统计学意义；t检验的前提是，两组数据来自正态分布的群体，数据的方差齐，满足独立性。

独立样本t检验（各实验处理组之间毫无相关存在，即为独立样本），该检验用于检验两组非相关样本被试所获得的数据的差异性。
独立样本t检验统计量为：

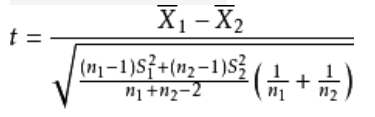
S1²和 S2²为两样本方差；n₁ 和n₂ 为两样本容量。

选用的检验方法必须符合其适用条件。理论上，即使样本量很小时，也可以进行t检验。（如样本量为10，一些学者声称甚至更小的样本也行），只要每组中变量呈正态分布，两组方差不会明显不同。如上所述，可以通过观察数据的分布或进行正态性检验估计数据的正态假设。
方差齐性的假设可进行F检验，或进行更有效的Levene’s检验。如果不满足这些条件，可以采用校正的t检验，或者换用非参数检验代替t检验进行两组间均值的比较。

什么是方差齐性检验？
你想一下，如果两组数据，我们仅仅比较他们的平均数有什么用呢？我们实际想做的是：这两组数据所表达的意思相差有多远，这不仅仅包括平均数，但是我们能做的，分析的有限，所以我们要保证各组数据是正态分布，且方差齐性，想想正态分布函数，就只有两个参数，一个是方差，一个是平均数，如果在总体是正太分布的前提下，方差齐性，就只差检验平均数，如果平均数也差异不大，则我们可得知这两组数据我表达的意思差异不显著。试想一下，两组数据仅仅是平均数相等，而其他什么都不确定，比如说方差差异显著，那仅仅平均数相等能说明的问题有限 。

方差的意义在于反映了一组数据与其平均值的偏离程度。
方差齐性检验的原理：
除了对两个研究总体的总体平均数的差异进行显著性检验以外，我们还需要对两个独立样本所属总体的总体方差的差异进行显著性检验，统计学上称为方差齐性（相等）检验。
对两个研究总体进行总体方差齐性的显著性检验，同两个总体平均数差异的显著性检验的步骤一样。

首先提出两个总体方差没有差异的零假设，即，和备择假设。然后从两个研究总体中各抽取容量分别为两个样本，通过比较两个样本方差之间的差异，来推断两个总体方差之间的差异。

方差是衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是各个数据分别与其平均数之差的平方的和的平均数。
方差的特性在于：方差是和中心偏离的程度，用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）并把它叫做这组数据的方差。 在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。
标准差是方差的算术平方根，意义在于反映一个数据集的离散程度。