Tensorflow模型量化(Quantization)原理及其实现方法

量化目的

压缩模型大小，加速模型推断速度，方便将深度学习模型部署到手机等计算资源受限的终端上。

量化分类

对称量化

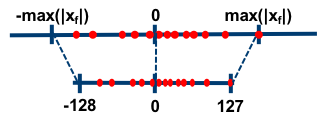
如上图所示，所谓的对称量化，即使用一个映射公式将输入数据映射到[-128,127]的范围内，图中-max(|Xf|)表示的是输入数据的最小值，max(|Xf|)表示输入数据的最大值。对称量化的一个核心即零点的处理，映射公式需要保证原始的输入数据中的零点通过映射公式后仍然对应[-128,127]区间的零点。总而言之，对称量化通过映射关系将输入数据映射在[-128,127]的范围内，对于映射关系而言，我们需要求解的参数即Z和S。
在对称量化中，r 是用有符号的整型数值(int8)来表示的，此时 Z=0，且 q=0时恰好有r=0。在对称量化中，我们可以取Z=0，S的取值可以使用如下的公式，也可以采用其它的公式。

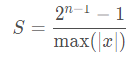
其中，n 是用来表示该数值的位宽，x 是数据集的总体样本。

非对称量化

如上图所示，所谓的非对称量化，即使用一个映射公式将输入数据映射到[0,255]的范围内，图中min(Xf)表示的是输入数据的最小值，max(Xf)表示输入数据的最大值。总而言之，对称量化通过映射关系将输入数据映射在[0,255]的范围内，对于映射关系而言，我们需要求解的参数即Z和S。
  在非对称量化中，r 是用有符号的整型数值(uint8)来表示的。在非对称量化中，我们可以取Z=min(x)，S的取值可以使用如下的公式，也可以采用其它的公式。
  

原理详解

模型量化桥接了定点与浮点，建立了一种有效的数据映射关系，使得以较小的精度损失代价获得了较好的收益，要弄懂模型量化的原理就是要弄懂这种数据映射关系。
浮点转换为定点的公式如下所示：

定点转换为浮点的公式如下所示：

其中R表示输入的浮点数据，Q表示量化之后的定点数据，Z表示Zero Point的数值，S表示Scale的数值，我们可以根据S和Z这两个参数来确定这个映射关系。求解S和Z有很多种方法，这里列举中其中的一种求解方式如下：

具体案例

训练后的模型权重或激活值往往在一个有限的范围内分布，如激活值范围为[-2.0, 6.0]，然后我们使用int8进行模型量化，则定点量化值范围为[-128, 127]，那么S和Z的求值过程如下所示：

如果此时我们有一个真实的激活值为0.28即R=0.28，那么对应Q的求解过程如下所示：

整个网络中的其它参数也按照这种方法就可以获得量化之后的数值。

模型量化实现步骤

对于模型量化任务而言，具体的执行步骤如下所示：

步骤1-在输入数据（通常是权重或者激活值）中统计出相应的min_value和max_value;
步骤2-选择合适的量化类型，对称量化（int8）还是非对称量化（uint8）；