关于sinX与y的大小比较取值范围计算

关于sinX与y的大小比较取值范围计算

@(概率论)

在求分布函数的时候，常常有已知$X$的分布函数求$Y=g(X)$的分布函数类型。往往不小心就会计算出错误的范围，从而导致分布函数求错。

比如：$X \in [0,\pi]$

则$sinX \leq y$的范围是什么？

注意，在概率论中常常用大写字母表示变量，小写字母表示取值。

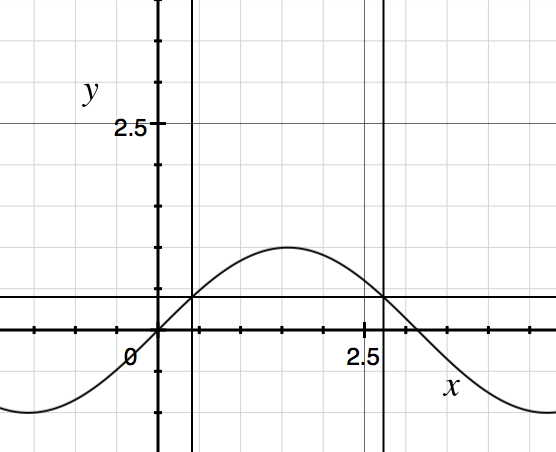
有两个角度的思考，根据$sinX$的图像推导：

可知两个交点是：$X = arcsiny, \pi-arcsiny$

那么再根据图像可知取值范围是：$X \in[0,arcsiny] \cup [\pi-arcsiny,\pi]$

这种思路很清晰明确且不易出错。

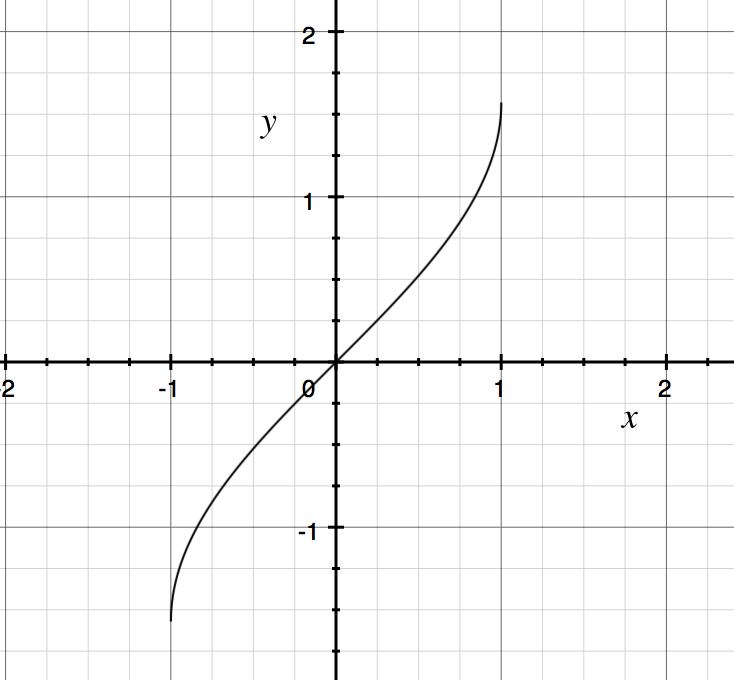
但当熟悉反函数的图像时：$X = arcsiny$

因为反函数是个函数，也是一一映射，所以不能反映$[\frac{\pi}{2},\pi]$上的取值，因此，不可以直接化为$X \leq arcsiny$.

简单说就是，sinx在R上并没有反函数，需要限定取值范围才可以。这里可以分成$x\in[0,\frac{\pi}{2}]\cup [\frac{\pi}{2},\pi]$两部分讨论，但是没有直接在sinX的图像上研究更容易把握。