【深度学习-吴恩达】L2-1 深度学习的实践

L2 改善深层神经网络

1 深度学习的实践

课程时长105min25s

1.1 训练集&验证集&测试集

应用深度学习是一个迭代的过程

• 小数据阶段

  • 验证集和测试集占比较大
  • 70%实验集，30%测试集
  • 60%实验集，20%验证集，20%测试集

• 大数据阶段

  • 验证集和测试集占比减小

• 确保验证集和测试集的数据来自同一分布

• 没有测试集也是可行的

  • 验证集作为测试集
  • 此时应用于不需要进行无偏估计

1.2 偏差&方差

Bias&Variance

欠拟合、适度拟合、过拟合

• 训练集错误率1%，测试集错误率11%：方差较大
• 训练集错误率15%，测试集错误率16%：偏差较大
  • 拟合训练集不佳
• 训练集错误率15%，测试集错误率30%：方差较大且偏差较大
• 训练集错误率0.5%，测试集错误率1%：方差较小且偏差较小

1.3 机器学习基础

1. 是否有较高的偏差？
   • 用于验证训练集性能
   • 如果有，则尝试改变网络结构或使用其他类型网络
2. 是否具有较高的方差？
   • 用于验证测试集性能
   • 如果有，采用更多的数据或者正则化方法

1.4 正则化

Regularization

减小方差的方法，避免过度拟合

• 在logistic回归中
  $$\begin{gathered} \underset{w,b}{\min }J(w,b) \\ J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^i)+\frac{\lambda }{2m}||w|{|}_2^2 \\ ||w|{|}_2^2=\sum _{j=1}^{n_x}{w}_j^2=w^{T}w \end{gathered}$$

  • 下标2指的是L2正则化

    • 被称为权重衰减

  • L1正则化
    $$\frac{\lambda }{m}\sum _{j=1}^{n_x}|w_j|=\frac{\lambda }{m}||w|{|}_1$$

    • 如果使用L1正则化，则w结果会是稀疏的
    • w中有很多0

  • b为实数，因此在正则化中可以进行省略

  • λ为正则化参数

• 在神经网络中
  $$\begin{gathered} J(w^{[1]},b^{[1]},\dots ,w^{[L]},b^{[L]})=\frac{1}{m}\sum _{i=1}^{m}l({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}\sum _{l=1}^L||w^{[l]}|{|}_F^2 \\ ||w^{[l]}|{|}_F^2=\sum _{i=1}^{n^{[l-1]}}\sum _{j=1}^{n^{[l]}}(w_{i,j}^{[l]}{)}^2,whichw:(n^{[l-1]},n^{[l]}) \end{gathered}$$

  • 下标F表示Frobenius范数

  • 将正则化加入计算中
    $$\begin{gathered} d{w}^{[l]}=(frombackpop)+\frac{\lambda }{m}{w}^{[l]} \\ {w}^{[l]}=w^{[l]}-\alpha d{w}^{[l]}=w^{[l]}-\frac{\alpha \lambda }{m}{w}^{[l]}-\alpha (frombackpop) \end{gathered}$$

1.5 为什么正则化可以减少过拟合

• 若正则化λ参数较大，权重矩阵$w$被设置为接近0的值
  • 神经网络神经元数量减少，深度不变
  • 从过拟合状态倾向于向Logistic回归进行移动
• 使用tanh函数作为激活函数
  • 若$w$绝对值较小，则利用tanh函数接近线性部分
  • 如果正则化参数较大，则$w$较小，导致z^[l]较小，从而使得接近线性部分，不适用于复杂决策

1.6 Dropout正则化

随机失活

对每层神经元，设置一个概率，随机删除神经元，使用删除后的神经元进行学习

• 反向随机失活：如一个三层神经网络

  # 以（1 - keep-prob）概率失活
  d3 = np.random.rand(a3.shape[0],a3.shape[1])< keep-prob
  a3 = np.multiply(a3, d3) #a3 * d3
  a3 /= keep-prob #使得削减神经元之后a的期望值不变
  

1.7 理解Dropout

Dropout功能类似L2正则化

• 由于神经元的输入中将会被随机消除某几个，所以不能依赖某个神经元的输入特征

不同层的keep-prob可以不同

计算机视觉中应用较广

在绘制损失函数图像时候要设置为1，不然不能正常绘制

1.8 其他正则化函数

增大数据集

• 对数据集进行变换
  • 图片翻转、裁剪、旋转、扭曲

提前终止 early stopping

• 训练过程中测试验证集
• 在中间停止
• 缺点：不能独立解决损失函数和方差较大问题

1.9 归一化输入

1. 零均值化
   $$\begin{gathered} \mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)} \\ x:=x-\mu \end{gathered}$$

2. 归一化方差
   $$\begin{gathered} {\sigma }^2=\frac{1}{m}\sum _{i=1}^M{x}^{(i{)}^2} \\ x/=\sigma \end{gathered}$$

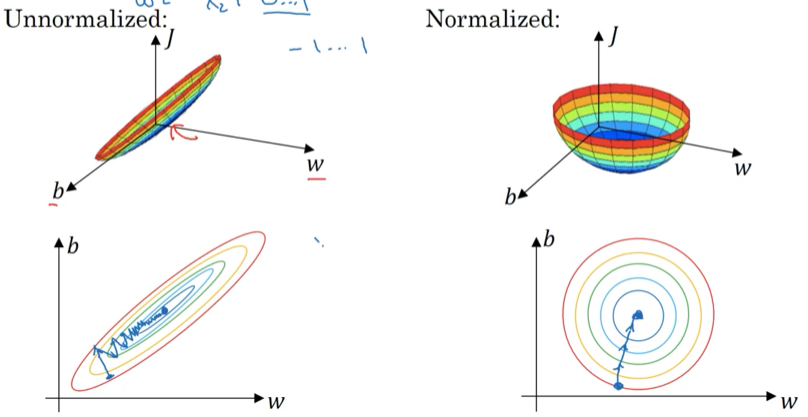
为什么归一化输入

• 方便找到极值

  

1.10 梯度消失和梯度爆炸

在较深的神经网络中

• 若$w$大于1，容易造成梯度爆炸
• 若$w$小于1，容易造成梯度消失

1.11 神经网络的权重初始化

一个不彻底的解决梯度消失和梯度爆炸的方法

• ReLU函数
  $$W^{[l]}=np.random.randn(shape)\ast np.sqrt(\frac{2}{n^{[l-1]}})$$

• tanh函数
  $$\begin{gathered} W^{[l]}=np.random.randn(shape)\ast np.sqrt(\frac{1}{n^{[l-1]}}) \\ or{W}^{[l]}=np.random.randn(shape)\ast np.sqrt(\frac{1}{n^{[l-1]}+n^{[l]}}) \end{gathered}$$

1.12 梯度的数值逼近

导数的定义

使用双边误差更为准确：
$$\frac{f(\theta +\xi )-f(\theta -\xi )}{2\xi }$$

1.13 梯度检验

假设网络中参数：$W^{[1]},b^{[1]},W^{[2]},b^{[2]},\dots ,W^{[L]},b^{[L]}$

将所有参数设置为向量$\theta$

则$J(W^{[1]},b^{[1]},W^{[2]},b^{[2]},\dots ,W^{[L]},b^{[L]})=J(\theta )=J({\theta }_1,{\theta }_2,\dots )$

同理，将参数$d{W}^{[1]},d{b}^{[1]},d{W}^{[2]},d{b}^{[2]},\dots ,d{W}^{[L]},d{b}^{[L]}$

设置为$d\theta$

则for each i：
$$d{\theta }_{approx}^{[i]}=\frac{J({\theta }_1,{\theta }_2,\dots ,{\theta }_i+\xi ,\dots )-J({\theta }_1,{\theta }_2,\dots ,{\theta }_i-\xi ,\dots )}{2\xi }$$
进行梯度检验：
$$\frac{||d{\theta }_{approx}-d\theta |{|}_2}{||d{\theta }_{approx}|{|}_2+||d\theta |{|}_2},inwhich\xi =10^{-7}$$
得到结果：

• ≈10^-7：Great
• ≈10^-5：Maybe is OK
• ≈10^-3：Bug

1.14 关于梯度校验实现

• 不要在训练中使用梯度校验，仅仅用于调试
• 如果算法的梯度校验失败，要检查所用项
• 梯度检验时候，使用正则化
• 梯度检验不能和Dropout同时使用
• 随机初始化过程中，可以进行梯度检验
  • 保证$w,b$有一段时间远离0