<<Signals and systems>> Chapter 2
Linear Time-Inverariant Systems
2.1 Discrete-time LTI system: the convolution sum
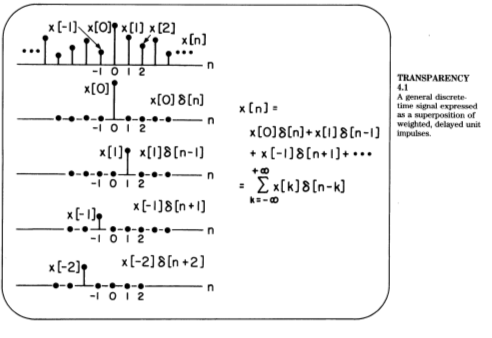
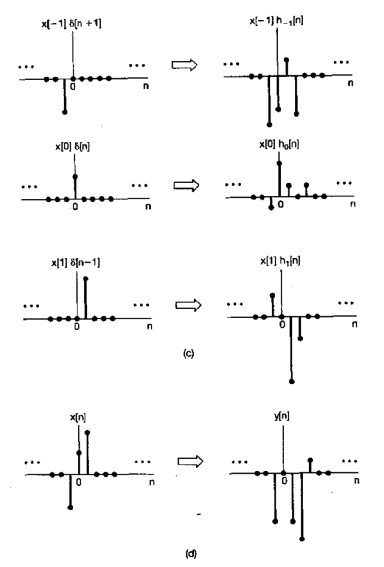
离散的信号可以用叠合的不同幅值的delta函数表示出来
The discret-time unit impulse response and the convolution sum representation of LTI systems
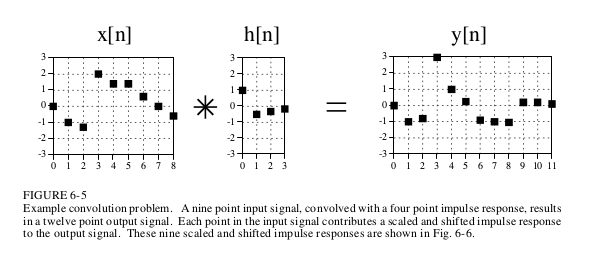
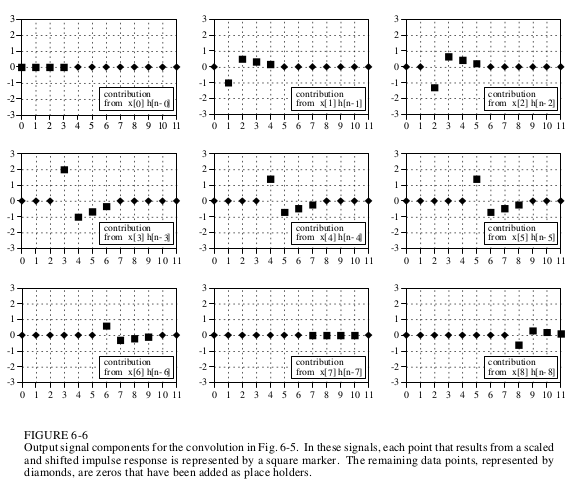
上面的例子很清楚的一步步的解析了卷积和的过程.
卷积和的部分可以去看看我写的这篇《Why should we use convolution?》
对于为什么是x[k]*h[n-k]
这里研究的是LTI系统,h[n]是LTI系统,对于不同时刻k输入x[k],系统的响应仅仅做偏移即可,
x[0]输入的对应h为h[0],x[1]对应的h为h[n-1]... x[k] 对应的就是h[n-k]
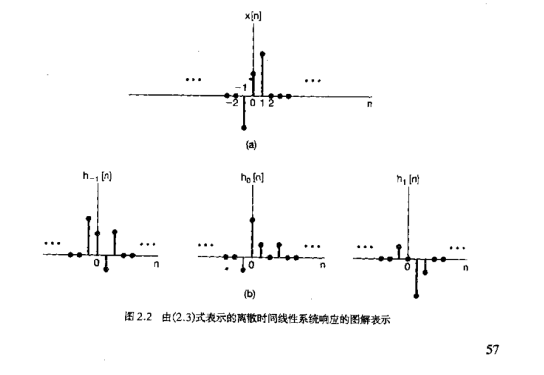
为了加深概念的理解,我们再看看时变系统卷积和的过程
输入是X[n],响应是h,注意时变系统的输入响应不同时刻不同,所以这里有三个不同的响应
我们把输入看作impluse 序列,这样,利用delta函数的性质,就很容易get到输出了哇~
要知道对系统输入的是一系列的impulse,于是应该把所有结果(x[-1]h[-1], ...,x[1]h[1])累加起来,得到输出y[n],
这就是为什么下面y[n]卷积和公式里面会有连加符号的原因!
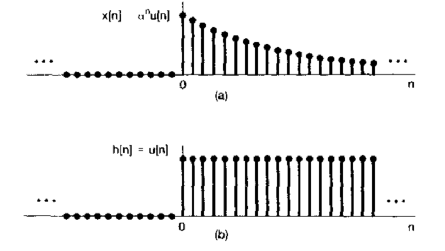
而正是由于时变系统的特性,会导致一种有趣的现象,对于输入x[n]和响应h[n]
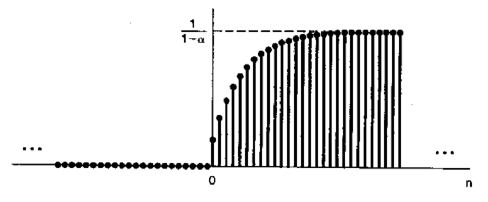
计算过程中直接把h[n]反转,然后偏移k个单位,直接于原来的输入信号做乘法,然后把各个单位的结果做累加,得到的就是此刻的输出y[n],最后系统的输出这里书上有一定的“误导性”,之所以打双引号是因为这里h[n]是一个无限长的step function,所以后面无穷逼近于1/(1-alpha).
在计算机中,不可能用无穷序列来模拟...输入序列就是有限的,那么输出就会是
(length of x[n]) + (length of h[n]) -1。
为什么会是减一?想想,如果输出到(length of x[n]) + (length of h[n])个点的时候,两者已经没有重叠区域,于是得到的结果是0.这里我们不考虑这个没有意义的点.于是输出就只有(length of x[n]) + (length of h[n]) -1个点
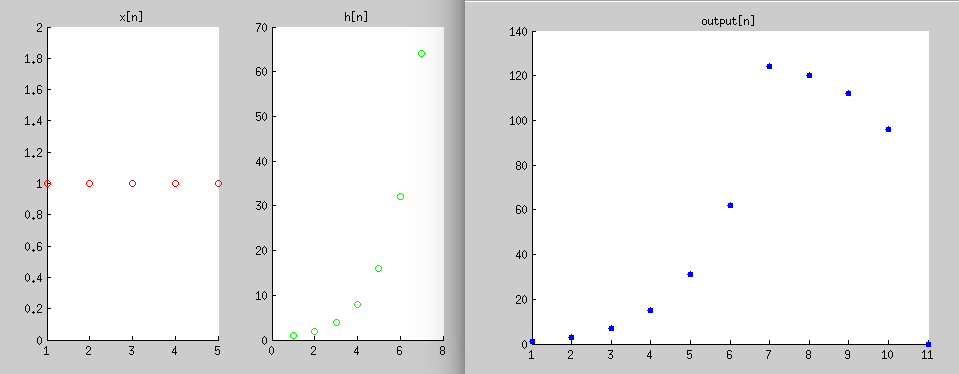
这里我做了个例子
%code writer : EOF
%code date : 2014.10 .1
%e-mail : jasonleaster@gmail.com
%code file : demo_for_convolution
%code purpose:
% A demo for convolution in LTI-system
clear all
close all
% you could use this varible to define how many number of points in the input sequence.
points = 10;
% x is used as input points
% h is used as responce sequnce.
% %% input sequence one
% x = exp(-[0: (points-1)]);
% h = ones(1,points*10);
%% Input sequence two
alpha = 2;
x = [1 1 1 1 1];
h = alpha.^([0:6]);
length_x = size(x,2);
length_h = size(h,2);
figure(1);
subplot(121);
scatter(1:length_x,x,'r');
title('x[n]');
subplot(122);
scatter(1:length_h,h,'g');
title('h[n]');
output = zeros(1,length_x+length_h -1);
%% Kernel part of our convolution sum :- )
for current_point_n= 1:length_x + length_h
tmp = current_point_n;
while(tmp > 0)
if current_point_n <= length_x && (current_point_n - tmp + 1) <= length_h
output(current_point_n) = output(current_point_n) + x(tmp)*h(current_point_n - tmp + 1);
end
if current_point_n > length_x && current_point_n < (length_h + length_x -1)
if tmp > length_x
tmp = tmp -1;
continue;
else
if (current_point_n - tmp + 1) <= length_h
output(current_point_n) = output(current_point_n) + x(tmp)*h(current_point_n - tmp + 1);
end
end
end
tmp = tmp -1;
end
end
figure(2);
scatter(1:size(output,2),output,'filled');
title('output[n]');
上面的输入随意调整都性,程序还是比较健壮的
Properties of LTI systems
交换律,结合律,分配律
对于可逆性的说明demo:

对于因果性的探讨,
稳定性的探究:
最后,要认识到,微分方程和差分方程仅仅是分别对于连续和离散系统的输入输出关系的描述而已,他们相似于都是对系统输入输出的描述,不可混淆对比.之前我胡乱的做对比,以至于很苦恼
这里记录了我思考的过程
http://blog.csdn.net/cinmyheart/article/details/39499967









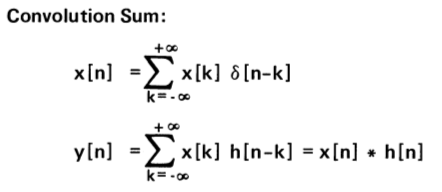





















 1857
1857

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








