平行平面层波导的声传播波动方程
感谢辜磊大佬群内分享相关书籍资料。感兴趣的请关注辜磊大佬的微信公众号:声学世界
声波在边界受限制的空间中传播,被称为波导中的声传播。声波在波导中传播,由于边界的限制,在边界限制方向取某些特定的驻波形式,而在无限制方向为行波形式。成为给定波导中的正简波。
假设简谐声波在
x
=
0
x=0
x=0和
x
=
h
x=h
x=h平行界面所限介质中传播,建立如下图的坐标。
则波动方程为
- ∂ 2 p ( x , z , t ) ∂ x 2 + ∂ 2 p ( x , z , t ) ∂ z 2 − 1 c 2 ∂ 2 p ( x , z , t ) ∂ t 2 = 0 \displaystyle \frac{{{{\partial }^{2}}p(x,z,t)}}{{\partial {{x}^{2}}}}+\frac{{{{\partial }^{2}}p(x,z,t)}}{{\partial {{z}^{2}}}}-\frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}p(x,z,t)}}{{\partial {{t}^{2}}}}=0 ∂x2∂2p(x,z,t)+∂z2∂2p(x,z,t)−c21∂t2∂2p(x,z,t)=0
对于简谐声波, p ( x , z , t ) = p ( x , z ) e j ω t \displaystyle p(x,z,t)=p(x,z){{e}^{{j\omega t}}} p(x,z,t)=p(x,z)ejωt,则有
- ∂ 2 p ( x , z ) ∂ x 2 + ∂ p ( x , z ) ∂ z 2 + k 2 p ( x , z ) = 0 \displaystyle \frac{{{{\partial }^{2}}p(x,z)}}{{\partial {{x}^{2}}}}+\frac{{\partial p(x,z)}}{{\partial {{z}^{2}}}}+{{k}^{2}}p(x,z)=0 ∂x2∂2p(x,z)+∂z2∂p(x,z)+k2p(x,z)=0
方程式的解为
- p ( x , z ) = ∑ n ( A n e − j k n x x + B n e j k n x x ) ( C n e − j k n z z + D n e j k n z z ) \displaystyle p(x,z)=\sum\limits_{n}{{({{A}_{n}}{{e}^{{-j{{k}_{{n{{x}^{x}}}}}}}}+{{B}_{n}}{{e}^{{j{{k}_{{n{{x}^{x}}}}}}}})}}({{C}_{n}}{{e}^{{-j{{k}_{{n{{z}^{z}}}}}}}}+{{D}_{n}}{{e}^{{j{{k}_{{n{{z}^{z}}}}}}}}) p(x,z)=n∑(Ane−jknxx+Bnejknxx)(Cne−jknzz+Dnejknzz)
式中: k n x 2 + k n z 2 = k 2 \displaystyle k_{{nx}}^{2}+k_{{nz}}^{2}={{k}^{2}} knx2+knz2=k2
在z方向只有正向传播的行波,所以 D n = 0 D_n =0 Dn=0在 x x x方向收到限制,声波在 x = 0 x=0 x=0和 x = h x=h x=h的界面反射,因此x方向反应驻波的特点。
- p ( x , z ) = ∑ n A n ′ cos ( k n x x ) + B n ′ sin ( k n x x ) ] e − j k n z Z \displaystyle p(x,z)=\sum\limits_{n}{{A_{{_{n}}}^{'}\cos ({{k}_{{nx}}}x)+B_{n}^{'}\sin ({{k}_{{nx}}}x)]{{e}^{{-j{{k}_{{nz}}}Z}}}}} p(x,z)=n∑An′cos(knxx)+Bn′sin(knxx)]e−jknzZ
对于绝对硬边界条件有
- u x ( x , z ) ∣ x = 0 , x = h = 0 \displaystyle {{u}_{x}}(x,z){{|}_{{x=0,x=h}}}=0 ux(x,z)∣x=0,x=h=0
于是带入公式可求
- p ( x , z ) = ∑ n = 0 ∞ A n cos ( n π h x ) ⋅ e − j z k 2 + ( n π h ) 2 , n = 0 , 1 , 2 , 3... \displaystyle p(x,z)=\sum\limits_{{n=0}}^{\infty }{{{{A}_{n}}\cos (\frac{{n\pi }}{h}x)\cdot {{e}^{{-jz\sqrt{{{{k}^{2}}+{{{(\frac{{n\pi }}{h})}}^{2}}}}}}}}},n=0,1,2,3... p(x,z)=n=0∑∞Ancos(hnπx)⋅e−jzk2+(hnπ)2,n=0,1,2,3...
带入时间因子
- p ( x , z , t ) = ∑ n = 0 ∞ A n cos ( n π h x ) ⋅ e − j z k 2 + ( n π h ) 2 ⋅ e j ω t , n = 0 , 1 , 2 , 3... \displaystyle p(x,z,t)=\sum\limits_{{n=0}}^{\infty }{{{{A}_{n}}\cos (\frac{{n\pi }}{h}x)\cdot {{e}^{{-jz\sqrt{{{{k}^{2}}+{{{(\frac{{n\pi }}{h})}}^{2}}}}}}}\cdot {{e}^{{j\omega t}}}}},n=0,1,2,3... p(x,z,t)=n=0∑∞Ancos(hnπx)⋅e−jzk2+(hnπ)2⋅ejωt,n=0,1,2,3...
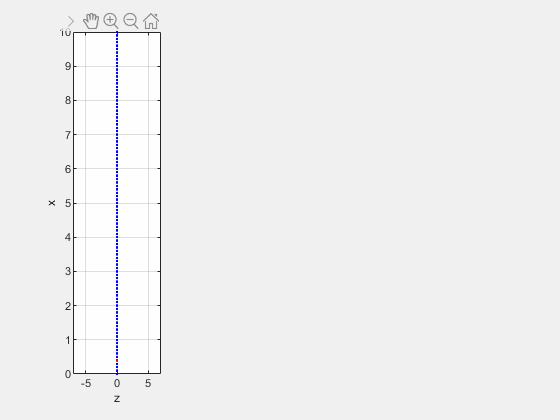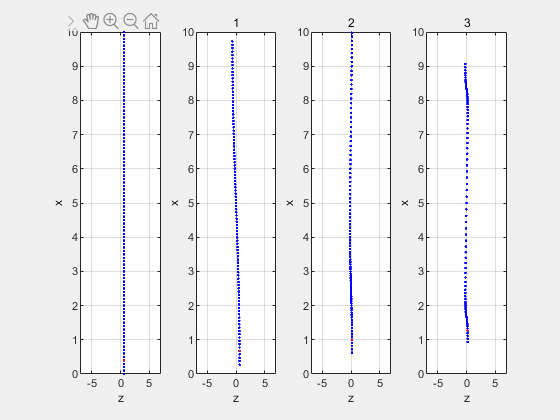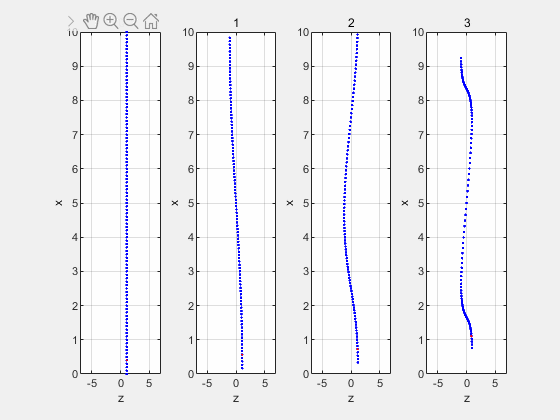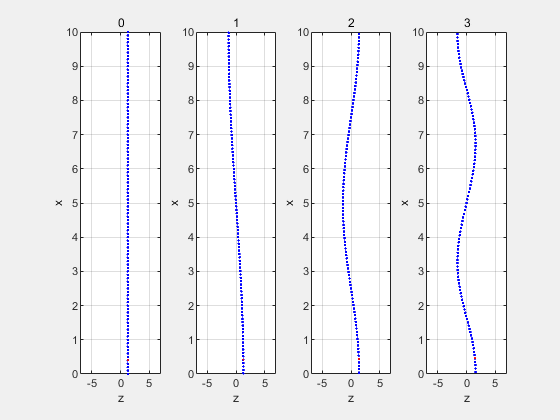
由上述公式可知各阶简正波的声压幅值为
- A n cos ( n π h x ) \displaystyle {{A}_{n}}\cos (\frac{{n\pi }}{h}x) Ancos(hnπx)
令
A
n
=
1
A_n=1
An=1仿真得到各阶简正波声压分布图
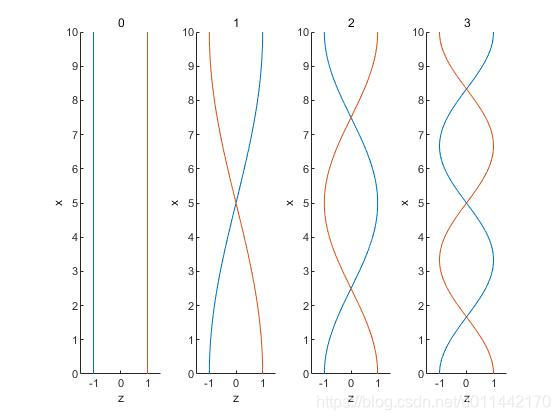
clc
clear
h=10;
c=1500;
f=300;
omega=2*pi*f;
k=omega/c;
An=1;
x=0:0.1:10;
z=0;
% 设简谐声波在x=0和x=10平行界面所限介质中传播
figure('Name','简谐声波平行界面振动','NumberTitle','off');
for n=0:3
subplot(1,4,n+1)
hold on;
plot(z-cos(n*pi*x/h),x)
hold on;
plot(z+cos(n*pi*x/h),x)
xlabel('z')
ylabel('x')
str=num2str(n);
title(str)
axis([-1.5 1.5 0 10])
end
前四阶简正波场中某质点运动位置
Copyright © 2020 by RichardYang. All rights reserved.
仅供参考,严禁转载,感谢。

























 1455
1455

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








