数据结构与算法系列之一：八大排序之基数排序

---

• 转载请注明作者和出处：http://blog.csdn.net/u011475210
• 个人博客：https://wordzzzz.github.io/ && https://wordzzzz.gitee.io/
• 代码地址：https://github.com/WordZzzz/Note/tree/master/DS-A
• 博客作者：WordZzzz，一只热爱技术的文艺青年

---

基数排序

前言

  建议先看排序综述，传送门：数据结构与算法系列之一：八大排序综述。

简介

  基数排序（英语：Radix sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机（Tabulation Machine）上的贡献。

  基数排序法会使用到桶 (Bucket)，顾名思义，通过将要比较的位（个位、十位、百位…），将要排序的元素分配至 0~9 个桶中，借以达到排序的作用，在某些时候，基数排序法的效率高于其它的比较性排序法。

步骤

  它是这样实现的：

• 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。
• 然后，从最低位开始，依次进行一次排序。
• 这样从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列。

  基数排序的方式可以采用LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。

演示

  wordzzzz的小数据规模演示：

代码

/*
 * 获取数组a中最大值
 */
template<typename T>
int get_max(T *array, const int length)
{
    int i, max;

    max = array[0];
    for (i = 1; i < length; i++)
        if (array[i] > max)
            max = array[i];
    return max;
}

/*
 * 对数组按照"某个位数"进行排序(桶排序)
 */
template<typename T>
void count_sort(T *array, const int length, int exp)
{
    T* output = (T*)malloc(sizeof(T) * length);

    if (output == NULL)
    {
        fputs("Error: out of memory\n", stderr);
        abort();
    }
    int i, buckets[10] = { 0 };

    for (i = 0; i < length; i++)                    // 将数据出现的次数存储在buckets[]中
        buckets[(array[i] / exp) % 10]++;

    for (i = 1; i < 10; i++)                        // 更改buckets[i]。目的是让更改后的buckets[i]的值，是该数据在output[]中的位置。
        buckets[i] += buckets[i - 1];

    for (i = length - 1; i >= 0; i--)               // 将数据存储到临时数组output[]中，这里的对应关系一定要捋清楚
        output[--buckets[(array[i] / exp) % 10]] = array[i];

    for (i = 0; i < length; i++)                    // 将排序好的数据赋值给array[]
        array[i] = output[i];
}

/*
 * 基数排序
 */
template<typename T>
void RadixSort(T *array, const int length)
{
    int exp;                                        // 指数。当对数组按各位进行排序时，exp=1；按十位进行排序时，exp=10；...
    int max = get_max(array, length);               // 数组array中的最大值

    for (exp = 1; max / exp > 0; exp *= 10)         // 从个位开始，对数组array按"指数"进行排序
        count_sort(array, length, exp);
}

算法复杂度

• 数据结构 数组
• 平均时间复杂度 $O(d*(n+r))$
• 最好情况 $O(d*(n+r))$
• 最坏情况 $O(d*(n+r))$
• 空间复杂度 $O(n+r)$

  其中，d 为位数，r 为基数，n 为原数组个数。在基数排序中，因为没有比较操作，所以在复杂上，最好的情况与最坏的情况在时间上是一致的，均为 O(d*(n + r))。

分析

  如果捋不清上述代码中的数组对应关系，可以参考一下下面这两张图的讲解，来源：http://www.cnblogs.com/skywang12345/p/3603669.html。

• 个位的数值范围是[0,10)。因此，参见桶数组buckets[]，将数组按照个位数值添加到桶中。

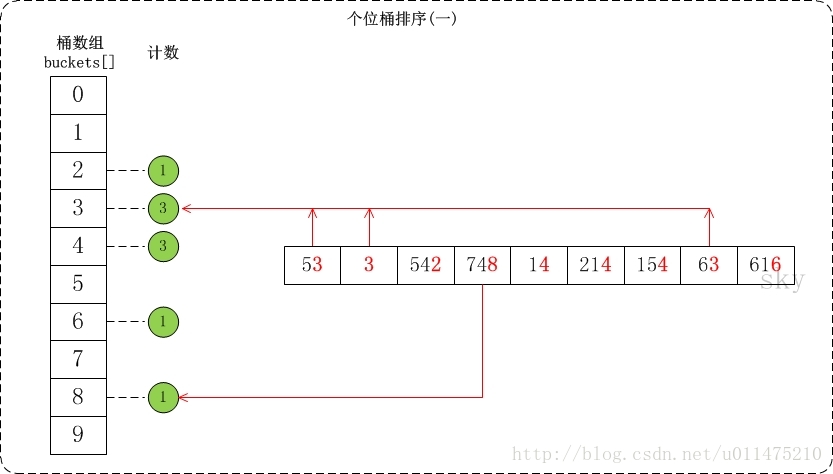
• 接着是根据桶数组buckets[]来进行排序。假设将排序后的数组存在output[]中；找出output[]和buckets[]之间的联系就可以对数据进行排序了。

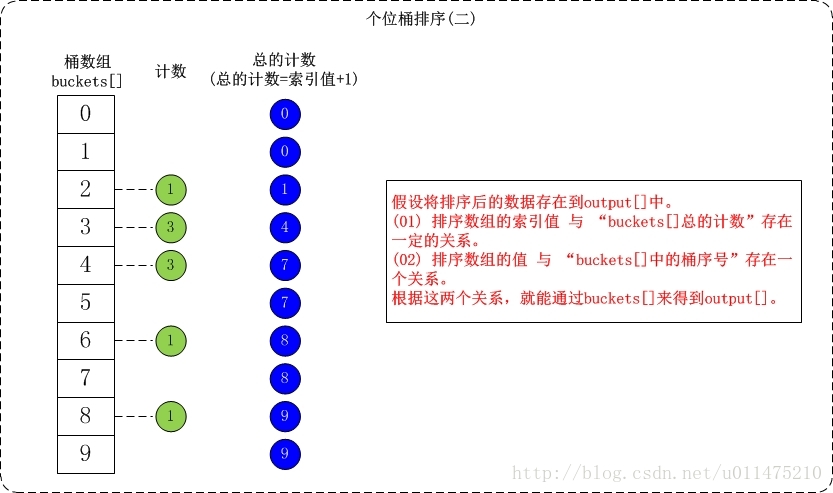
  基数排序不改变相同元素之间的相对顺序，因此它是稳定的排序算法。

  基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序：根据键值的每位数字来分配桶
• 计数排序：每个桶只存储单一键值
• 桶排序：每个桶存储一定范围的数值

系列教程持续发布中，欢迎订阅、关注、收藏、评论、点赞哦～～(￣▽￣～)～

完的汪(∪｡∪)｡｡｡zzz