题目描述:
如何判断一个点是否在一个三角形内。
测试样例:

自定义的POINT类:
class POINT{
int x;
int y;
public POINT(int x,int y){
this.x = x;
this.y = y;
}
}
思路一:
面积法:
如果一个点在三角形内,其与三角形的三个点构成的三个子三角形的面积等于大三角形的面积。否则,大于大三角形的面积。
所以,这个问题就转化成如何在知道三角形的三个点的情况下,求这个三角形的面积的问题了。
因为所有点的坐标已知,我们有几种方式计算面积:
1)首先可以计算出每条边的长度及周长,我们就可以利用海伦公式计算面积,然后进行比较。
S = p ( p − a ) ( p − b ) ( p − c ) S = \sqrt{p(p-a)(p-b)(p-c)} S=p(p−a)(p−b)(p−c)
p = ( a + b + c ) 2 p = \frac{(a+b+c)}{2} p=2(a+b+c)
2)向量法:先求出这个三角形的对应的平行四边形的面积。然后这个面积的1/2就是三角形的面积了。
先随意选择两个点,如B、C通过其坐标相减得向量(B,C)。记得谁减另一个就是指向谁。然后求出其中一个点和剩下一个点的向量。这两个向量的叉乘的便是平行四边形的面积。除以2就是三角形的面积。(注意这里是叉乘 (cross product),而非点乘(dot product))。
(补充)向量之间的积分为两种:叉乘和点乘。叉乘求面积,点乘求投影。这是两者的意义。而且,叉乘理论得到的是一个向量,而点乘得到的是一个标量。


代码:
private static final double ABS_DOUBLE_0 = 0.0001;
public static boolean isInTriangle(POINT A, POINT B, POINT C, POINT P) {
double ABC = triAngleArea(A, B, C);
double ABp = triAngleArea(A, B, P);
double ACp = triAngleArea(A, C, P);
double BCp = triAngleArea(B, C, P);
double sumOther = ABp + ACp + BCp;
if (-ABS_DOUBLE_0 < (ABC - sumOther) && (ABC - sumOther) < ABS_DOUBLE_0) { // 若面积之和等于原三角形面积,证明点在三角形内
return true;
} else {
return false;
}
}
private static double triAngleArea(POINT A, POINT B, POINT C) { // 由三个点计算这三个点组成三角形面积
POINT ab,bc;
ab = new POINT(B.x - A.x,B.y - A.y);//
bc = new POINT(C.x - B.x,C.y - B.y);
return Math.abs((ab.x * bc.y - ab.y * bc.x) / 2.0);
}
思路二:
同向法:
假设点P位于三角形内,会有这样一个规律,当我们沿着ABCA的方向在三条边上行走时,你会发现点P始终位于边AB,BC和CA的右侧。我们就利用这一点,但是如何判断一个点在线段的左侧还是右侧呢?我们可以从另一个角度来思考,当选定线段AB时,点C位于AB的右侧,同理选定BC时,点A位于BC的右侧,最后选定CA时,点B位于CA的右侧,所以当选择某一条边时,我们只需验证点P与该边所对的点在同一侧即可。问题又来了,如何判断两个点在某条线段的同一侧呢?可以通过叉积来实现,连接PA,将PA和AB做叉积,再将CA和AB做叉积,如果两个叉积的结果方向一致,那么两个点在同一测。

代码:
public static boolean isInTriangle(POINT A, POINT B, POINT C, POINT P) {
/*利用叉乘法进行判断,假设P点就是M点*/
int a = 0, b = 0, c = 0;
POINT MA = new POINT(P.x - A.x,P.y - A.y);
POINT MB = new POINT(P.x - B.x,P.y - B.y);
POINT MC = new POINT(P.x - C.x,P.y - C.y);
/*向量叉乘*/
a = MA.x * MB.y - MA.y * MB.x;
b = MB.x * MC.y - MB.y * MC.x;
c = MC.x * MA.y - MC.y * MA.x;
if((a <= 0 && b <= 0 && c <= 0)||
(a > 0 && b > 0 && c > 0))
return true;
return false;
}
思路三:
重心法:
我们都知道,三角形的三个点在同一个平面上,如果选中其中一个点,其他两个点不过是相对该点的位移而已,比如选择点A作为起点,那么点B相当于在AB方向移动一段距离得到,而点C相当于在AC方向移动一段距离得到。

所以对于平面内任意一点,都可以由如下方程来表示。
P = A + u ∗ ( C − A ) + v ∗ ( B − A ) P = A + u * (C-A) + v * (B-A) P=A+u∗(C−A)+v∗(B−A)
如果系数u或v为负值,那么相当于朝相反的方向移动,即BA或CA方向。那么如果想让P位于三角形ABC内部,u和v必须满足什么条件呢?有如下三个条件:
u >= 0
v >= 0
u + v <= 1
几个边界情况:
当u = 0,v = 0 时,就是点A;
当u = 0,v = 1 时,就是点B;
当u = 1,v = 0 时,就是点C。
整理方程1得到:
P − A = u ( C − A ) + v ( B − A ) P-A = u(C-A) + v(B-A) P−A=u(C−A)+v(B−A)
令 v0 = C – A, v1 = B – A, v2 = P – A,则
v 2 = u ∗ v 0 + v ∗ v 1 v2 = u * v0 + v * v1 v2=u∗v0+v∗v1
现在是一个方程,两个未知数,无法解出u和v,所以将等式两边分别点乘v0和v1的到两个等式:(ps.下面公式中的·符号代表“点乘”)
( v 2 ) ⋅ v 0 = ( u ∗ v 0 + v ∗ v 1 ) ⋅ v 0 (v2)·v0 = (u * v0 + v * v1)·v0 (v2)⋅v0=(u∗v0+v∗v1)⋅v0
( v 2 ) ⋅ v 1 = ( u ∗ v 0 + v ∗ v 1 ) ⋅ v 1 (v2)·v1 = (u * v0 + v * v1)·v1 (v2)⋅v1=(u∗v0+v∗v1)⋅v1
注意到这里u和v是数,而v0,v1和v2是向量,所以可以将点积展开得到下面的式子。
v 2 ⋅ v 0 = u ∗ ( v 0 ⋅ v 0 ) + v ∗ ( v 1 ⋅ v 0 ) v2·v0 = u * (v0·v0) + v * (v1·v0) v2⋅v0=u∗(v0⋅v0)+v∗(v1⋅v0)
v 2 ⋅ v 1 = u ∗ ( v 0 ⋅ v 1 ) + v ∗ ( v 1 ⋅ v 1 ) v2·v1 = u * (v0·v1) + v * (v1·v1) v2⋅v1=u∗(v0⋅v1)+v∗(v1⋅v1)
解这个方程得到:
u = ( ( v 1 ⋅ v 1 ) ( v 2 ⋅ v 0 ) − ( v 1 ⋅ v 0 ) ( v 2 ⋅ v 1 ) ) / ( ( v 0 ⋅ v 0 ) ( v 1 ⋅ v 1 ) − ( v 0 ⋅ v 1 ) ( v 1 ⋅ v 0 ) ) u = ((v1·v1)(v2·v0)-(v1·v0)(v2·v1)) / ((v0·v0)(v1·v1) - (v0·v1)(v1·v0)) u=((v1⋅v1)(v2⋅v0)−(v1⋅v0)(v2⋅v1))/((v0⋅v0)(v1⋅v1)−(v0⋅v1)(v1⋅v0))
v = ( ( v 0 ⋅ v 0 ) ( v 2 ⋅ v 1 ) − ( v 0 ⋅ v 1 ) ( v 2 ⋅ v 0 ) ) / ( ( v 0 ⋅ v 0 ) ( v 1 ⋅ v 1 ) − ( v 0 ⋅ v 1 ) ( v 1 ⋅ v 0 ) ) v = ((v0·v0)(v2·v1)-(v0·v1)(v2·v0)) / ((v0·v0)(v1·v1) - (v0·v1)(v1·v0)) v=((v0⋅v0)(v2⋅v1)−(v0⋅v1)(v2⋅v0))/((v0⋅v0)(v1⋅v1)−(v0⋅v1)(v1⋅v0))
代码
private static boolean isInTriangle(POINT p, POINT a, POINT b, POINT c) {
POINT AB, AC, AP;
AB = new POINT(b.x - a.x, b.y - a.y);
AC = new POINT(c.x - a.x, c.y - a.y);
AP = new POINT(p.x - a.x, p.y - a.y);
float dot00 = dotProduct(AC, AC);
float dot01 = dotProduct(AC, AB);
float dot02 = dotProduct(AC, AP);
float dot11 = dotProduct(AB, AB);
float dot12 = dotProduct(AB, AP);
float inverDeno = 1 / (dot00 * dot11 - dot01 * dot01);
// 计算重心坐标
float u = (dot11 * dot02 - dot01 * dot12) * inverDeno;
float v = (dot00 * dot12 - dot01 * dot02) * inverDeno;
return (u >= 0) && (v >= 0) && (u + v < 1);
}
private static float dotProduct(POINT p1, POINT p2) {
return p1.x * p2.x + p1.y * p2.y;
}
------至所有正在努力奋斗的程序猿们!加油!!
有码走遍天下 无码寸步难行
1024 - 梦想,永不止步!
爱编程 不爱Bug
爱加班 不爱黑眼圈
固执 但不偏执
疯狂 但不疯癫
生活里的菜鸟
工作中的大神
身怀宝藏,一心憧憬星辰大海
追求极致,目标始于高山之巅
一群怀揣好奇,梦想改变世界的孩子
一群追日逐浪,正在改变世界的极客
你们用最美的语言,诠释着科技的力量
你们用极速的创新,引领着时代的变迁
——乐于分享,共同进步,欢迎补充
——Treat Warnings As Errors
——Any comments greatly appreciated
——Talking is cheap, show me the code
——诚心欢迎各位交流讨论!QQ:1138517609
——CSDN:https://blog.csdn.net/u011489043
——简书:https://www.jianshu.com/u/4968682d58d1
——GitHub:https://github.com/selfconzrr







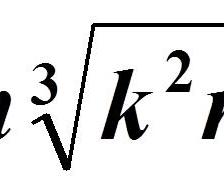
















 884
884

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










